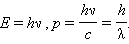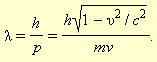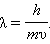Корпускулярно-волновой дуализм — физический принцип, согласно которому любой объект может проявлять как волновые, так и корпускулярные свойства. Был введён при разработке квантовой механики для объяснения явлений, наблюдаемых в микромире.
В частности, свет — это и корпускулы (фотоны), и электромагнитные волны. Свет демонстрирует свойства волны в явлениях дифракции и интерференции при масштабах, сравнимых с длиной световой волны. Например,одиночные фотоны, проходящие через двойную щель, создают на экране интерференционную картину, определяемую уравнениями Максвелла.[1]. Тем не менее, эксперимент показывает, что фотон не есть короткий импульс электромагнитного излучения, например, он не может быть разделён на несколько пучков оптическими делителями лучей. Корпускулярные свойства света проявляются при фотоэффектеи в эффекте Комптона. Фотон ведет себя и как частица, которая излучается или поглощается целиком объектами, размеры которых много меньше его длины волны (например, атомными ядрами), или вообще могут считаться точечными (например, электрон).
Во́лны де Бро́йля — волны, связанные с любой микрочастицей и отражающие их квантовую природу.
Для частиц не очень высокой энергии, движущихся со скоростью 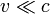 (скорости света), импульс равен
(скорости света), импульс равен 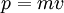 (где
(где 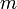 — масса частицы), и
— масса частицы), и 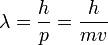 . Следовательно, длина волны де Бройля тем меньше, чем больше масса частицы и её скорость. Например, частице с массой в 1 г, движущейся со скоростью 1 м/с, соответствует волна де Бройля с
. Следовательно, длина волны де Бройля тем меньше, чем больше масса частицы и её скорость. Например, частице с массой в 1 г, движущейся со скоростью 1 м/с, соответствует волна де Бройля с 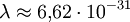 м, что лежит за пределами доступной наблюдению области. Поэтому волновые свойства несущественны в механике макроскопических тел. Для электронов же с энергиями от 1 эВ до 10 000 эВ длина волны де Бройля лежит в пределах от ~ 1 нм до 10-2 нм, то есть в интервале длин волн рентгеновского излучения. Поэтому волновые свойства электронов должны проявляться, например, при их рассеянии на тех же кристаллах, на которых наблюдается дифракция рентгеновских лучей.
м, что лежит за пределами доступной наблюдению области. Поэтому волновые свойства несущественны в механике макроскопических тел. Для электронов же с энергиями от 1 эВ до 10 000 эВ длина волны де Бройля лежит в пределах от ~ 1 нм до 10-2 нм, то есть в интервале длин волн рентгеновского излучения. Поэтому волновые свойства электронов должны проявляться, например, при их рассеянии на тех же кристаллах, на которых наблюдается дифракция рентгеновских лучей.
Первое подтверждение гипотезы де Бройля было получено в 1927 году в опытах американских физиков К. Дэвиссона и Л. Джермера. Пучокэлектронов ускорялся в электрическом поле с разностью потенциалов 100—150 В (энергия таких электронов 100—150 эВ, что соответствует 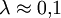 нм) и падал на кристалл никеля, играющий роль пространственной дифракционной решётки. Было установлено, что электроны дифрагируют на кристалле, причём именно так, как должно быть для волн, длина которых определяется соотношением де Бройля.
нм) и падал на кристалл никеля, играющий роль пространственной дифракционной решётки. Было установлено, что электроны дифрагируют на кристалле, причём именно так, как должно быть для волн, длина которых определяется соотношением де Бройля.
Подтвержденная на опыте идея де Бройля о двойственной природе микрочастиц — корпускулярно-волновом дуализме — принципиально изменила представления об облике микромира. Поскольку всем микрообъектам (по традиции за ними сохраняется термин «частица») присущи и корпускулярные, и волновые свойства, то, очевидно, любую из этих «частиц» нельзя считать ни частицей, ни волной в классическом понимании. Возникла потребность в такой теории, в которой волновые и корпускулярные свойства материи выступали бы не как исключающие, а как взаимно дополняющие друг друга. В основу такой теории — волновой, или квантовой, механики — и легла концепция де Бройля. Это отражается даже в названии «волновая функция» для величины, описывающей в этой теории состояние системы. Квадрат модуля волновой функции определяет вероятность состояния системы, и поэтому о волнах де Бройля часто говорят как о волнах вероятности (точнее, амплитуд вероятности). Для свободной частицы с точно заданным импульсом p (и энергией 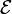 ), движущейся вдоль оси x, волновая функция имеет вид:
), движущейся вдоль оси x, волновая функция имеет вид:
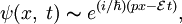
где 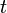 — время,
— время, 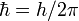 .
.
В этом случае 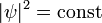 , то есть вероятность обнаружить частицу в любой точке одинакова.
, то есть вероятность обнаружить частицу в любой точке одинакова.
Французский физик Л. де Бройль выдвинул гипотезу об универсальности корпускулярно-волнового дуализма. Де Бройль утверждал, что не только фотоны, но и электроны и любые другие частицы материи наряду с корпускулярными обладают также и волновыми свойствами.
Согласно де Бройлю, с каждым микрообъектом связаны, с одной стороны, корпускулярные характеристики – энергия E и импульс p, а с другой стороны, волновые характеристики – частота ν и длина волны λ.
Корпускулярные и волновые характеристики микрообъектов связаны такими же количественными соотношениями, как и у фотона:
|
Гипотеза де Бройля постулировала эти соотношения для всех микрочастиц, в том числе и для таких, которые обладают массой m. Любой частице, обладающей импульсом, сопоставлялся волновой процесс с длиной волны λ = h / p. Для частиц, имеющих массу,
|
В нерелятивистском приближении (υ << c)
|
Французский ученый Луи де Бройль (1892–1987) в 1924 г. в докторской диссертации «Исследования по теории квантов» выдвинул смелую гипотезу об универсальности корпускулярно-волнового дуализма, утверждая, что поскольку свет ведет себя в одних случаях как волна, а в других – как частица, то и материальные частицы (электроны и др.) в силу общности законов природы должны обладать волновыми свойствами. «В оптике, – писал он, – в течение столетия слишком пренебрегали корпускулярным способом рассмотрения по сравнению с волновым; не делалась ли в теории вещества обратная ошибка? Не думали ли мы слишком много о картине «частиц» и не пренебрегали ли чрезмерной картиной волн?» В то время гипотеза де Бройля выглядела безумной. Лишь в 1927 г., три года спустя, наука пережила огромное потрясение: физики К. Дэвиссон и Л. Джермер экспериментально подтвердили гипотезу де Бройля, получив дифракционную картину электронов.
Согласно квантовой теории света А. Эйнштейна, волновые характеристики фотонов света (частота колебаний v ф, релятивистской массой mф и импульсом рф) соотношениями:
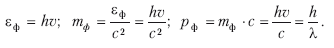
По идее де Бройля, любая микрочастица, в том числе и с массой покоя ш0 Ц 0, должна обладать не только корпускулярными, но и волновыми свойствами. Соответствующие частота v и длина волны л определяются при этом соотношениями, подобными эйнштейновским:
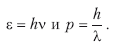
Отсюда длина волны де Бройля —
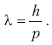
Таким образом, соотношения Эйнштейна, полученные им при построении теории фотонов в результате гипотезы, выдвинутой де Бройлем, приобрели универсальный характер и стали одинаково применимыми как для анализа корпускулярных свойств света, так и при исследовании волновых свойств всех микрочастиц.
Б). Свет обладает как волновыми, так и корпускулярными свойствами. Волновые свойства проявляются при распространении света (интерференция, дифракция). Корпускулярные свойства проявляются при взаимодействии света с веществом (фотоэффект, излучение и поглощение света атомами).
Свойства фотона как частицы (энергия E и импульс p) связаны с его волновыми свойствами (частотой ν и длиной волны λ) соотношениями
| E = hν; p = hν / c = h / λ, |
где h = 6,63·10–34 Дж·с – постоянная Планка.
Французский физик де Бройль в 1924 г. высказал предположение, что сочетание волновых и корпускулярных свойств присуще не только свету, но и любому материальному телу. Согласно де Бройлю, каждому телу массой m, движущемуся со скоростью υ, соответствует волновой процесс с длиной волны
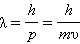
|
(нерелятивистское приближение υ << c).
Наиболее отчетливо волновые свойства проявляются у элементарных частиц. Это происходит потому, что из-за малой массы частиц длина волны оказывается сравнимой с расстоянием между атомами в кристаллических решетках. В этом случае при взаимодействии пучка частиц с кристаллической решеткой возникаетдифракция.
Для иллюстрации волновых свойств частиц часто используют мысленный эксперимент – прохождение пучка электронов (или других частиц) через щель ширинойΔx. С точки зрения волновой теории при дифракции на щели пучок будет уширяться с угловой расходимостью θ ≥ λ / Δx. С корпускулярной точки зрения уширение пучка после прохождения щели объясняется появлением у частиц некоторого поперечного импульса. Разброс значений этого поперечного импульса («неопределенность») есть
| Δpx ≈ pθ ≥ (λ / Δx)p = h / Δx. |
Соотношение
| Δpx · Δx ≥ h |
носит название соотношения неопределенностей. Это соотношение на корпускулярном языке выражает наличие волновых свойств у частиц.
Эксперимент по прохождению пучка электронов через две близко расположенные щели может служить еще более яркой иллюстрацией волновых свойств частиц. Этот эксперимент является аналогом оптического интерференционного опыта Юнга.
Компьютерная модель воссоздает на экране дисплея мысленные эксперименты по дифракции электронов на одной и двух щелях.
Подлетая к экрану со щелями, частицы взаимодействуют с ним как волны де Бройля. Поведение частиц в пространстве между экраном со щелями и фотопластинкой описывается в квантовой физике с помощью Ψ-функций. Квадрат модуля пси-функции определяет вероятность обнаружения частицы в том или ином месте. Таким образом, попадание частиц в различные точки фотопластинки есть вероятностный процесс. Компьютерная модель позволяет продемонстрировать этот процесс.
В случае одиночной щели модель иллюстрирует соотношение неопределенностей, которое является следствием двойственной природы частиц. Можно изменять в некоторых пределах ширину щели и наблюдать дифракционное размытие электронного пучка на фотопластинке.
Предполагается, что электроны имеют энергию порядка 100 эВ.
Обратите внимание, что в случае двух щелей наблюдаемое на фотопластинке распределение не является простым наложением двух независимых распределений от каждой из щелей в отдельности. Появление интерференционных полос на фотопластинке однозначно свидетельствует о том, что каждая достигшая фотопластинки частица одновременно прошла через обе щели экрана.
Дата: 2019-02-19, просмотров: 404.