Принцип неопределённости Гейзенбе́рга (или Га́йзенберга) в квантовой механике — фундаментальное неравенство (соотношение неопределённостей), устанавливающее предел точности одновременного определения пары характеризующих квантовую систему физических наблюдаемых, описываемых некоммутирующимиоператорами (например, координаты и импульса, тока и напряжения, электрического и магнитного поля). Соотношение неопределенностей задает нижний предел для произведения среднеквадратичных отклонений пары квантовых наблюдаемых.

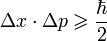
Если приготовлены несколько идентичных копий системы в данном состоянии, то измеренные значения координаты и импульса будут подчиняться определённому распределению вероятности — это фундаментальный постулат квантовой механики. Измеряя величину среднеквадратического отклонения Δx координаты и среднеквадратического отклонения Δp импульса, мы найдем что:

,

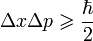где 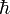— приведённая постоянная Планка. В некоторых случаях «неопределённость» переменной определяется как наименьшая ширина диапазона, который содержит 50 % значений, что, в случае нормального распределения переменных, приводит для произведения неопределённостей к большей нижней границе 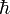. Отметьте, что это неравенство даёт несколько возможностей — состояние может быть таким, что x может быть измерен с высокой точностью, но тогда p будет известен только приблизительно, или наоборот p может быть определён точно, в то время как x — нет. Во всех же других состояниях, и x и p могут быть измерены с «разумной» (но не произвольно высокой) точностью.

В повседневной жизни мы обычно не наблюдаем неопределённость потому, что значение 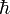чрезвычайно мало.

Обнаружение волновых свойств микрочастиц означает, что классическая механика не может дать правильного описания поведения микрообъектов. Новая физическая теория, устанавливающая законы движения и взаимодействия микрочастиц и фотонов с учетом их волновых и корпускулярных свойств, была разработана, главным образом, тремя физиками: Э. Шредингером (австр.), В. Гейзенбергом (нем.) и П. Дираком (англ.) в начале ХХ века и получила название волновой или квантовой механики.

В классической механике всякая частица движется по определённой траектории, так что ее координаты и импульс могут быть точно рассчитаны для любого момента времени. Совсем по иному обстоит дело, если рассматривается вопрос о локализации волнового процесса, т.е. о месте нахождения волны в данный момент времени. Ведь волна не имеет ни определенной траектории, ни определенной координаты. Т.о. возникает необходимость внести некоторые ограничения в применении к объектам микромира понятий классической механики.

Эти ограничения сформулированы Гейзенбергом и получили название соотношений неопределенностей. Основное из них гласит: чем точнее определены какие-либо из координат частицы, тем больше неопределенность в значении составляющей импульса (или скорости) в том же направлении, и наоборот. Количественно это записывается так:

Δx·Δp_x ≥ ђ Δx·Δυ_x ≥ ђ/m,

Δy·Δp_y ≥ ђ Δy·Δυ_y ≥ ђ/m, (3)

Δz·Δp_z ≥ ђ Δz·Δυ _z ≥ ђ/m,

где Δx, Δy, Δz – неопределенности координат; Δp_x, Δp_y, Δp_z – неопределенности проекций импульса на оси – x, y, z; Δυ_x, Δυ_y , Δυ_z – неопределенности проекций скоростей на соответствующие оси; m – масса микрочастицы; ђ = h/2π – постоянная Планка с крышечкой.

Из соотношения неопределенностей следует: если положение частицы точно известно (Δx=0), то в этом состоянии проекция импульса на ось х-ов совершенно не определена (Δp_х → ∞), и наоборот.

Покажем, что соотношение неопределенностей действительно вытекает из волновых свойств микрочастиц. Рассмотрим мысленный опыт по дифракции потока электронов на щели шириной Δx ~ λ, расположенной перпендикулярно к направлению движения частиц (рис. 3).

Д о прохождения через щель p_х = 0; ∆p_х = 0, а координатаxне определена, т.е. ∆x→ ∞. В момент прохождения через щель координата электрона имеет неопределенность ∆xравную ширине щели. В то же время, из-за дифракции, электроны отклоняются от первоначального направления и будут двигаться в пределах угла 2φ, где φ – угол дифракции. Теперь появляется неопределенность в значении составляющей импульса вдоль осиx-ов:

∆p_х = p∙sinφ = h sinφ /λ_Б . (4)

Если даже ограничиться электронами, попадающими на экран в пределах центрального максимума, то sinφ найдем из условия 1-ого минимума на щели (bsinφ = kλ, где b – ширина щели, k – порядок минимума):

∆x∙sinφ = λ_Б. (5)

Подставляя выражение для sinφ в (4), после преобразования получим

Δx·Δp_x = h (6)

Учитывая главные max более высоких порядков, куда тоже попадают электроны, окончательно будем иметь:

Δx·Δp_x ≥ h ≥ ђ (7)

Следует подчеркнуть, что невозможность одновременного и точного определения координаты и соответствующей составляющей импульса не связана с несовершенством наших знаний или неточностью приборов, а является следствием специфических и вместе с тем объективных свойств микрообъектов.

Проиллюстрируем оценку границ применимости теории на примерах.

1. Скорость движения электрона в электроннолучевой трубке составляет υ_х=10⁶ м/с и определена с точностью до Δυ_х=10² м/с. Тогда неопределенность координаты:

Δx·Δυ_x ≥ ђ/m, .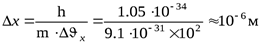

Т.е. в данном случае можно говорить о точке падения каждого отдельного электрона на экран и о траектории.

1. Скорость движения электрона в атоме водорода υ_х ~ 10⁶ м/с, неопределенность координаты порядка диаметра атома Δx = d ~10^-10 м. Тогда неопределенность величины скорости

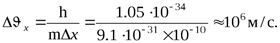
Т.е. неопределенность скорости соизмерима с самой скоростью. Это означает, что электрон не может теперь рассматриваться как дискретная частица.

Соотношение неопределенностей может быть записано для любой пары взаимосвязанных характеристик состояния микрочастиц, например, для энергии и времени пребывания в этом энергетическом состоянии:

ΔЕ·Δt ≥ ђ. (8)

Из данного соотношения видно, что разброс энергии ΔЕ = ђ/Δt возрастает с уменьшением среднего времени пребывания системы в состоянии с энергией Е. Отсюда, следует, что частота излученного фотона также должна иметь неопределенность:

Δv = ΔЕ / h, (9)

т.е. линии спектра, обусловленные переходом электронов между уровнями Е₁и Е₂ с ΔЕ = Е₁– Е₂, будут иметь размытие по частоте равное Δv= v₀ ±ΔЕ / h, что подтверждается опытом.