В квантовой теории движения квантовых частиц в силовых полях для волновых функций используют принцип суперпозиции состояний.

Этот принцип обобщает все известные опытные факты, о движении квантовых частиц в силовых полях.

Принцип суперпозиции состояний позволяет описать волновые явления в терминах корпускулярных представлений ценой отказа от некоторых классических понятий, взятых из макроскопических опытов и не применимых к микропроцессам в квантовой механике.

Рассмотрим явление отражения, и преломления волн на границе раздела двух сред с корпускулярной точки зрения.

Согласно корпускулярно-волновому дуализму падающей волне отвечают частицы с импульсом

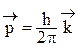, (4.1)

а отраженной и преломленной волнам - частицы с импульсами

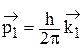
и

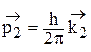. (4.2)

Так как частота волн при отражении и преломлении не изменяется, то частицы в каждой из волн имеют одинаковую энергию

W = W₁ = W₂ = hn. (4.3)

Если предположить, что на границу раздела двух сред падает одна частица, то возникает вопрос, в какой из волн, отраженной или преломленной, она окажется.

Корпускулярно-волновое описание (в отличие от волнового описания, позволяющего падающей волне разделиться на две) не допускает разделения одной падающей частицы на две, т. к. при этом нарушился бы закон сохранения энергии.

Согласно теории вероятности, частица может быть случайным образом, либо в отраженной волне, либо в преломленной волне.

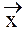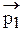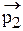Обозначим символом | ñ состояние частицы, возникающее в результате взаимодействия падающей частицы с границей раздела двух сред, а символами | ñ и | ñ - состояния частицы, отвечающие отраженной и преломленной волнам с единичными амплитудами.

Поэтому в состоянии | 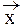ñ существует вероятность обнаружить частицы, как в отраженной, так и преломленной волне.

Описание процесса в терминах корпускулярных представлений может быть получено, если состояние | 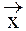ñ является суперпозицией состояни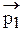й | ñ и | 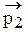ñ, т. е.

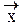| ñ = С₁ | 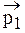ñ + С₂ | 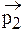ñ, (4.4)

причем квадраты коэффициентов |С₁|² и |С₂|² пропорциональны вероятностям обнаружить частицу в соответствующих состояниях.

Суперпозиция состояний (4.4) принципиально отличается от суперпозиции каких-либо полей или волн.

Для того чтобы корпускулярное объяснение сохранило фазовые соотношения между соответствующими волнами, необходимо, чтобы в качестве коэффициентов С₁ и С₂ в (4.4) использовать комплексные числа и, что физический смысл имеет разность фаз комплексных чисел.

Таким образом, для полного описания волнового явления с корпускулярных позиций необходимо приписать физический смысл не только вероятностям |С₁|² и |С₂|², но и самим коэффициентам С₁ и С₂, называемыми амплитудами вероятности, с точностью до общей фазы.

При этом для измерения разности фаз амплитуд вероятности необходимы интерференционные опыты.

Таким образом, если возможными являются состояния Y₁, Y₂, …, Y_n, то существуют также состояния

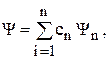(4.5)

где с_n (n = 1, 2, …) - некоторые комплексные числа.

Суперпозиция тех состояний Y(р), которые определяются значениями некоторой физической величины р, изменяющейся непрерывно, а не дискретно, находится не суммированием, а интегрированием:

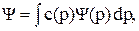(4.6)

где с(р) - некоторая комплексная функция переменной р.

Суперпозицию состояний, отличающихся значениями внутренней характеристики частиц, называют поляризацией состояний.

Поляризация представляет собой чисто волновое свойство, поскольку она определяется направлением колебаний в волне.

Тем не менее, частицам, соответствующим волне с определенной поляризацией, можно приписать дополнительную степень свободы, принимающую различные значения для разных состояний поляризации.

Принцип суперпозиции состояний существует и в классической физике (например, при одновременном распространении волн малых амплитуд они складываются, не влияя друг на друга).

В квантовой физике принцип суперпозиции состояний имеет качественно новое содержание, из-за корпускулярно-волновых свойств частиц.

Например, принцип суперпозиции состояний допускает смешивание двух взаимоисключающих с классической точки зрения состояний частицы, в одном из которых импульс частицы противоположен импульсу частицы в другом состоянии.

Однако в этом отношении суперпозиция квантовых состояний лишена наглядности.

Волновая функция

Для описания вероятности нахождения частицы в данный момент времени в некоторой точке пространства вводят волновую функцию (амплитуду вероятности) y(х, у, z, t).

Поэтому вероятность dw того, что частица находится в элементе объема dV, пропорциональна |y|², т. е.

dw = |y|²dV

или

dw = |y|²dxdydz. (4.7)

Физический смысл имеет не сама волновая функция y(х, у, z, t), а квадрат ее модуля

|y|² = yy^*,

где y^* - функция, комплексно сопряженная с y, т. е. величина |y|² имеет смысл плотности вероятности

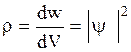, (4.8)

которая определяет вероятность появления частицы в данной точке пространства.

Следовательно, |y|² определяет интенсивность волн де Бройля.

Пребывание частицы, где-либо в пространстве - достоверное событие и его вероятность равна единице, т. е. должно выполняться условие нормировки

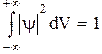. (4.9)

Вывод: Волновая функция (амплитуда вероятности) y(х, у, z, t) является основной характеристикой состояния квантовой системы.

Движение любой квантовой частицы можно описать волновым уравнением. Статистическое истолкование волн де Бройля и соотношений неопределенностей Гейзенберга указывают на то, что уравнение движения частицы в квантовой механике должно быть таким, чтобы оно позволяло объяснить наблюдаемые на опыте волновые свойства частиц.

Состояние частицы в данный момент времени в пространстве определяется в квантовой механике заданием волновой функции y(х, у, z, t), точнее величиной |y|², определяющей вероятность нахождения частицы в некоторой точке с координатами х, у, z в данный момент времени t.

Поэтому основное уравнение квантовой механики должно быть уравнением относительно волновой функции (х, у, z, t) и играть роль волнового уравнения, решения которого позволяли бы объяснить эксперименты, например, по дифракции микрочастиц, указывающих на их волновые свойства.

Следует отметить, что процессе экспериментов выявился факт взаимодействия микрочастицы с измерительным прибором, т. е. сам человек, проводящий эксперимент влияет на результат опыта.