Звуковыми (или акустическими) волнами
называются распространяющиеся в среде упругие волны, обладающие частотами в пределах 16—20000Гц. Волны указанных частот, воздействуя на слуховой аппарат человека, вызывают ощущение звука. Волны с v< 16 Гц (инфразвуковые) и v> >20 кГц (ультразвуковые) органами слуха человека не воспринимаются.
Звуковые волны в газах и жидкостях могут быть только продольными, так как эти среды обладают упругостью лишь по отношению к деформациям сжатия (растяжения). В твердых телах звуковые волны могут быть как продольными, так и поперечными, так как твердые тела обладают упругостью по отношению к деформациям сжатия (растяжения) и сдвига.
Интенсивностью звука (или силой звука) называется величина, определяемая
средней по времени энергией, переносимой звуковой волной в единицу времени сквозь единичную площадку, перпендикулярную направлению распространения волны:
I=W/(St).
Единица интенсивности звука в СИ — ватт на метр в квадрате (Вт/м2).
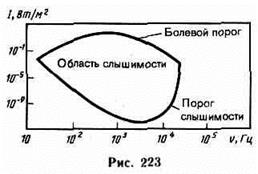
Чувствительность человеческого уха различна для разных частот. Для того чтобы вызвать звуковое ощущение, волна должна обладать некоторой минимальной интенсивностью, но если эта интенсивность превышает определенный предел, то звук не слышен и вызывает только болевое ощущение. Таким образом, для каждой частоты колебаний существует наименьшая (порог слышимости) и наибольшая (порог болевого ощущения) интенсивность звука, которая способна вызвать звуковое восприятие. На рис. 223 представлена зависимость порогов слышимости и болевого ощущения от частоты звука. Область, расположенная между этими двумя кривыми, является областью слышимости.
Если интенсивность звука является величиной, объективно характеризующей волновой процесс, то субъективной характеристикой звука, связанной с его интенсивностью, является громкость звука, зависящая от частоты. По физиологическому закону Вебера — Фехнера, с ростом интенсивности звука громкость возрастает по логарифмическому закону. На этом основании вводят объективную оценку громкости звука по измеренному значению его интенсивности:
L=lg(I/I0),
где I0 — интенсивность звука на пороге слышимости, принимаемая для всех зву-
250
ков равной 10-12 Вт/м2. Величина L называется уровнем интенсивности звука
и выражается в белах (в честь изобретателя телефона Белла). Обычно пользуются единицами, в 10 раз меньшими,— децибелами (дБ).
Физиологической характеристикой звука является уровень громкости, который выражается в фонах (фон). Громкость для звука в 1000 Гц (частота стандартного чистого тона) равна 1 фон, если его уровень интенсивности равен 1 дБ. Например, шум в вагоне метро при большой скорости соответствует »90 фон, а шепот на расстоянии 1 м— »20 фон.
Реальный звук является наложением гармонических колебаний с большим набором частот, т. е. звук обладает акустическим спектром, который может быть сплошным (в некотором интервале присутствуют колебания всех частот) и линейчатым (присутствуют отделенные друг от друга определенные частоты).
Звуковое ощущение характеризуется помимо громкости еще высотой и тембром. Высота звука — качество звука, определяемое человеком субъективно на слух и зависящее от частоты звука. С ростом частоты высота звука увеличивается, т. е. звук становится «выше». Характер акустического спектра и распределения энергии между определенными частотами определяет своеобразие звукового ощущения, называемое тембром звука. Так, различные певцы, берущие одну и ту же ноту, имеют различный акустический спектр, т. е. они имеют различный тембр.
Источником звука может быть всякое тело, колеблющееся в упругой среде со звуковой частотой (например, в струнных инструментах источником звука является струна, соединенная с корпусом инструмента).
Совершая колебания, тело вызывает колебания прилегающих к нему частиц среды с такой же частотой. Состояние колебательного движения последовательно передается к все более удаленным от тела частицам среды, т. е. в среде распространяется волна с частотой колебаний, равной частоте ее источника, и с определенной скоростью, зависящей от плотности и упругих свойств среды. Скорость распространения звуковых волн в газах вычисляется по формуле
v= Ö ( g RT/M), (158.1)
где R — молярная газовая постоянная, М — молярная масса, g= Cp/Cv — отношение молярных теплоемкостей газа при постоянных давлении и объеме, Т — термодинамическая температура. Из формулы (158.1) вытекает, что скорость звука в газе не зависит от давления р газа, но возрастает с повышением температуры. Чем больше молярная масса газа, тем меньше в нем скорость звука. Например, при T=273 К скорость звука в воздухе (M=29•10-3 кг/моль) v=331 м/с, в водороде (М=2•10-3 кг/моль) v=1260 м/с. Выражение (158.1) соответствует опытным данным.
При распространении звука в атмосфере необходимо учитывать целый ряд факторов: скорость и направление ветра, влажность воздуха, молекулярную структуру газовой среды, явление преломления и отражения звука на границе двух сред. Кроме того, любая реальная среда обладает вязкостью, поэтому наблюдается затухание звука, т. е. уменьшение его амплитуды и, следовательно, интенсивности звуковой волны по мере ее распространения. Затухание звука обусловлено в значительной мере его поглощением в среде, связанным с необратимым переходом звуковой энергии в другие формы энергии (в основном в тепловую).
Для акустики помещений большое значение имеет реверберация звука — процесс постепенного затухания звука в закрытых помещениях после выключения его источника. Если помещения пустые, то происходит медленное затухание звука и создается «гулкость» помещения. Если звуки затухают быстро (при применении звукопоглощающих материалов), то они воспринимаются приглушенными. Время реверберации — это время, в течение которого интенсивность звука в помещении ослабляется в миллион раз, а его уровень— на 60 дБ. Помещение обладает хорошей акустикой, если время реверберации составляет 0,5—1,5с.
Скорость звука в газах.
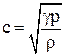 ,
,
где p – давление газа, не возмущенного волной;
r – плотность газа, не возмущенного волной;
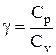 – отношение молярной теплоемкости газа при постоянном давлении к теплоемкости газа при постоянном объеме.
– отношение молярной теплоемкости газа при постоянном давлении к теплоемкости газа при постоянном объеме.
Амплитуда звукового давления Dp0 и амплитуда скорости v0 частиц в звуковой волне связаны соотношением
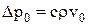 .
.
Интенсивность звука I, выраженная через амплитуду звукового давления – энергия, переносимая звуковой волной за единицу времени через единичную площадку, перпендикулярную направлению распространения волны:
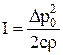 ,
,
где r – плотность газа.
Уровень интенсивности звука (в децибелах) определяется формулой
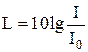 ,
,
где I – интенсивность данного звука;
I0 = 10–12 Вт/м2 – интенсивность звука на пороге слышимости при стандартной частоте n = 1 кГц.
Уровень громкости звука (в фонах) вычисляется по формуле
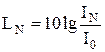 ,
,
где IN – интенсивность звука стандартной частоты n = 1 кГц, равногромкого с исследуемым звуком.
Явление Доплера – если источник и приемник звука перемещаются относительно среды, в которой распространяется звук, то частота звуковых колебаний n', регистрируемая приемником звука, связана с частотой собственных колебаний n источника соотношением
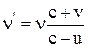 ,
,
где c, u, v – скорости соответственно звука, его источника и приемника.
Примечание. Записанная формула относится к случаю, если источник и приемник звука движутся по одной прямой. При этом величины u, v – алгебраические: u > 0, если источник движется к приемнику; u < 0, если источник удаляется от приемника. Аналогично v > 0, если приемник приближается к источнику; v < 0, если приемник движется от источника.
Вектор плотности потока энергии волны – физическая величина, модуль которой равен энергии DW, переносимой волной за единицу времени (Dt = 1) через единичную площадку, расположенную перпендикулярно направлению распространения волны (DS^):
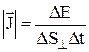 ;
; 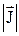 = u v; J = u×v,
= u v; J = u×v,
где u – плотность энергии в каждой точке среды, среднее значение которой вычисляется по формуле 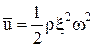 ;
;
ρ – плотность среды;
x0 – амплитуда волны;
w – круговая (циклическая частота);
v – фазовая скорость (скорость перемещения фазы волны).
Энергия, работа, мощность. Законы
сохранения в механике
Энергия – количественная мера и качественная характеристика движения и взаимодействия материи во всех ее превращениях. Она является функцией состояния системы и характеризует способности системы к совершению работы при переходе из одного состояния в другое.
Изменение энергии при переходе системы из одного состояния в другое равно работе, совершаемой системой в процессе перехода:
DW = W1 – W2 = A.
Диссипация (рассеяние) энергии механических систем –процесс перехода части их механической энергии в другие формы под влиянием внешних факторов (например, за счет наличия сил сопротивления).
Диссипативные системы – системы, в которых полная механическая энергия постепенно уменьшается за счет преобразования в другие (немеханические) формы, например в теплоту.
Механическая энергия – физическая величина, равная работе, которая может быть произведена при полном превращении движения данной формы в механическую форму движения материи.
Кинетическая энергия - физическая величина, характеризующая способность движущегося тела или системы совершать работу при торможении до полной остановки – одна из функций состояния ее движения:
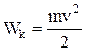 .
.
Кинетическая энергия системы – сумма кинетических энергий отдельных тел (материальных точек) этой системы:
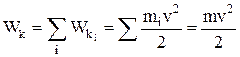 ,
,
где 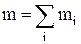 – масса тела (системы);
– масса тела (системы);
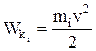 – кинетическая энергия i-го тела системы.
– кинетическая энергия i-го тела системы.
Связь между кинетической энергией тела (системы) и его импульсом:
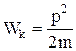 .
.
Кинетическая энергия при вращательном движении:
1) элементарной массы Dmi:
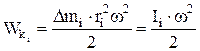 ,
,
где Ii = Dmi∙ri2 – момент инерции материальной точки, относительно выбранной оси вращения;
2) тела (системы):
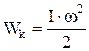 ,
,
где 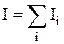 – момент инерции тела относительно той же оси вращения.
– момент инерции тела относительно той же оси вращения.
Потенциальная энергия–физическая величина, характеризующая способность системы совершать работу, связанную с изменением конфигурации и взаимного расположения тел или частей в системе.
Изменение потенциальной энергии системы зависит только от начального и конечного ее состояний и равно работе внутренних (консервативных) сил системы, взятой с обратным знаком:
dWp = –dA.
Характеристики поля тяготения – напряженность и потенциал поля тяготения.
Напряженностью поля тяготения в данной точке называется векторная физическая величина, равная по величине и направлению силе, действующей на единичную массу, помещенную в данную точку поля:
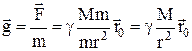 .
.
Потенциалом поля тяготения называют скалярную физическую величину, равную потенциальной энергии единичной массы, помещенной в данную точку поля:
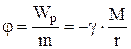 ,
,
т.е. потенциал поля тяготения тоже с увеличением расстояния увеличивается и при r ® ¥ равен нулю.
Связь между напряженностью и потенциалом поля тяготения:
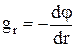 .
.
Дата: 2019-02-19, просмотров: 424.