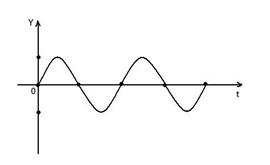
1. Колебания маятника в зависимости от угла его отклонения относительно вертикального положения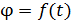

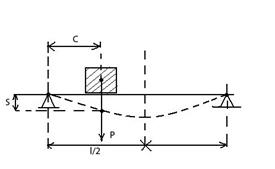
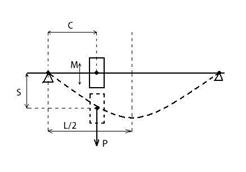
2. Изгибные колебания балки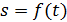

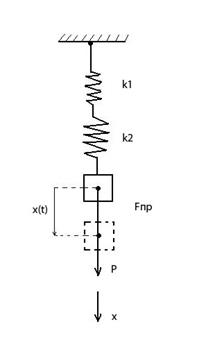
3. Колебания груза на пружине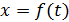

В зависимости от внешнего вида и причин возникновения различают следующие виды колебаний:

1. Детерминированные, случайные, хаотические;

2. Затухающие, стационарные, нарастающие (по виду графика);

3. Собственные, вынужденные, параметрические (по характеру внешнего воздействия).

Детерминированные колебания описываются функцией времени в форме аналитического выражения или графика, что позволяет определить его параметры в любой момент времени.

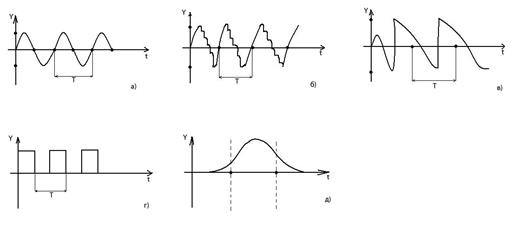
Рис 1. Детерминированные колебания

Детерминированные колебания могут носить периодический характер с периодом повторения Т или быть представлены в форме одиночного, непериодического колебания, рис 1, д.

Периодические колебания на интервале времени 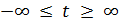можно представить в виде

,

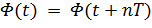где 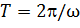–период колебаний; ω –круговая частота; 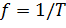–частота(1/с = Гц); n – положительное (отрицательное) число.

Периодические колебания разделяются на:

- гармонические (1, а) 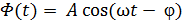, где А - амплитуда колебаний, 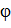- фаза;

- полигармонические (рис 1, б)

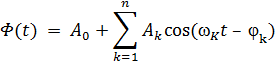
- релаксационные, в которых сравнительно медленные изменения состояния системы чередуется с быстрыми(скачкообразными). рис 1,в.

- импульсные колебания характеризуются наличием пауз между колебаниями, рис 1, г.

- затухающие колебания – колебания, амплитуда которых при t → ∞ стремится к нулю. Затухающие колебания описываются функцией.

,

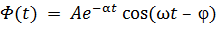где α - коэффициент затухания; А – амплитуда ; ω – частота; 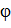-фазовый сдвиг.

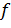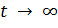- нарастающие колебания – амплитуда при неограниченно возрастает. Нарастающие колебания гармонической формы описываются функцией

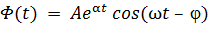, где α > 0

- стационарные колебания – колебания, амплитуда f,начиная с некоторого момента, постоянна:

,

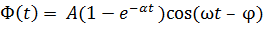где α > 0

Случайные колебания – колебания, в которых один или несколько параметров случайно зависят от времени и поэтому их относят к классу случайных процессов, рис. 2.а.

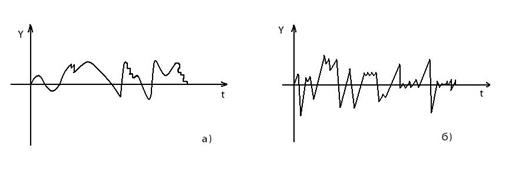
Рис. 2. Случайные колебания

Квазиупругие колебания. Дифференциальное уравнение и его решение. Кинематические характеристики колебательного движения.

Превращение энергии при идеальных гармонических колебаниях.

Примеры квазиупругих колебаний: пружинный маятник, физический маятник, математический маятник.

Сложение однонаправленных колебаний одинаковы частоты. Метод векторных диаграмм.

Сложение колебаний с близкими частотами. Биения.