Волновая поверхность – геометрическое место точек колеблющихся в одной фазе.

Фронт волны – пограничная волновая поверхность отделяющей среду возмущенную от среды невозмущенной.

По форме волновые поверхности:

-плоские

-сферические

-цилиндрические

Волновые поверхности плоских волн – совокупность параллельных плоскостей, перпендикулярных направлению распространения волны.

Для сферических волн, волновая поверхность - это концентрическая сфера.

Волновых поверхностей бесчисленное множество.

Фронт волны один и он всегда движется.

Фазовая скорость - это скорость распространения данной фазы колебаний, т.е. скорость волны.

Связь длины волны 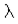, фазовой скорости периода колебаний Т задается соотношением:

.

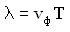
Длина волны – расстояние между ближайшими частицами, колеблющимися в одинаковой фазе.

Длина волны равна тому расстоянию, на которое распространяется определенная фаза колебания за период.

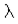=v*T

Волновое число — это отношение 2π радиан к длине волны, то есть это пространственный аналог круговой частоты ω

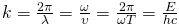
Волновым числом часто называют величину, обратную длине волны (1/λ), измеряемую обычно в обратных сантиметрах (см−1).

В формуле мы использовали :

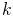— Волновое число

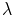— Длина волны

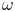—Угловая частота

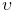—Фазовая скорость волны

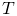— Период волны

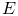—Энергия

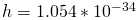—Постоянная Дирака

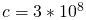—Скорость свете в вакууме

Плоская волна, распространяющаяся в произвольном направлении.

Получим уравнение плоской волны, распространяющейся в направлении, образующем с осями координат х, у, z углы α,β, γ Пусть колебания в плоскости, проходящей через начало координат, имеют вид .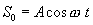

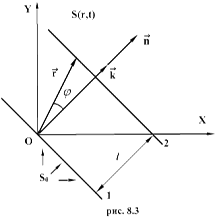
Возьмем волновую поверхность (плоскость), отстоящую от начала координат на расстоянии l. Колебания в этой плоскости будут отставать от колебаний в точке О (рис.8.3) на время 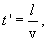тогда уравнение волны

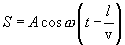
(8.4)

Выразим расстояние l через радиус-вектор 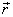точек рассматриваемой поверхности. Для этого введем единичный вектор 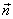нормали к волновой поверхности. Скалярное произведение

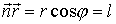
Подставим значение l в уравнение (8.4) и внесем в скобки

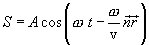
Отношение равно волновому числу k. Вектор 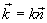равный по модулю волновому числу 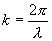и имеющий направление вдоль нормали к волновой поверхности называется волновым вектором. Введя вектор 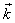, получим

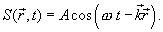
(8.5)

Чтобы перейти от радиуса - вектора точки к ее координатам х, у, z , выразим скалярное произведение 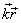через проекции векторов на координатные оси :

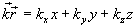
Тогда уравнение плоской волны принимает вид:

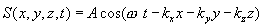
(8.6)

где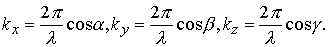

Волновое уравнение.

Распространение волн в однородной изотропной среде в общем случае описывается волновым уравнением - дифференциальным уравнением в частных производных.

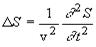, (4) где 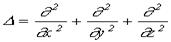(5)-оператор Лапласа, v - фазовая скорость.

Решением уравнения (4) является уравнение любой волны (плоской, сферической и т.д.). В частности, для анализируемой здесь плоской гармонической волны (1), которая не зависит от координат y и z волновое уравнение принимает вид 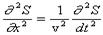. (6)

Cоответствующей подстановкой можно убедится, что уравнению (6) удовлетворяет уравнение (1).