При всяком изменении силы тока в про­водящем контуре возникает э.д.с. само­индукции, в результате чего в контуре появляются дополнительные токи, называ­емые экстратоками самоиндукции. Экстра­токи самоиндукции, согласно правилу Ленца, всегда направлены так, чтобы пре­пятствовать изменениям тока в цепи, т. е. направлены противоположно току, со­здаваемому источником. При выключении источника тока экстратоки имеют такое же направление, что и ослабевающий ток. Следовательно, наличие индуктивности в цепи приводит к замедлению исчезнове­ния или установления тока в цепи.

Рассмотрим процесс выключения тока в цепи, содержащей источник тока с э.д.с. ξ, резистор сопротивлением R и катушку индуктивностью L. Под дей­ствием внешней э.д.с. в цепи течет по­стоянный ток

I₀=ξ/R

(внутренним сопротивлением источника тока пренебрегаем).

В момент времени t=0 отключим источник тока. Ток через катушку индук­тивности L начнет уменьшаться, что при­ведет к возникновению э.д.с. самоиндук­ции ξ_s=-LdI/dt, препятствующей, со­гласно правилу Ленца, уменьшению тока. В каждый момент времени ток в цепи определяется законом Ома I=ξ_s/R, или

IR=-LdI/dt. (127.1)

Разделив в выражении (127.1) переменные, получим dI/I=-(R/L)dt. Интегрируя

это уравнение по I (от I₀ до I) и t (от 0 до t), находим ln(I/I₀)=-Rt/L, или

где t=L/R — постоянная, называемая временем релаксации. Из (127.2) следует, что т есть время, в течение которого сила тока уменьшается в е раз.

Таким образом, в процессе отключения источника э.д.с. сила тока убывает по экспоненциальному закону (127.2) и опре­деляется кривой 1 на рис. 183. Чем больше индуктивность цепи и меньше ее сопро­тивление, тем больше т и, следовательно, тем медленнее уменьшается ток в цепи при ее размыкании.

При замыкании цепи помимо внешней э.д.с.ξ возникает э.д.с. самоиндукции

ξ_s=-LdI/dt, препятствующая, согласно

правилу Ленца, возрастанию тока. По за­кону Ома, IR=ξ+ξ_s, или

IR=ξ-LdI/dt.

Введя новую переменную u=IR-ξ, пре­образуем это уравнение к виду du/u=-dt/ t ,

где 1 — время релаксации.

В момент замыкания (t=0) сила тока I=0 и u=-ξ. Следовательно, интегри­руя по и (от -ξ до IR — ξ) и t (от 0 до t).

находим ln(IR-ξ)/-ξ=-t/ t , или

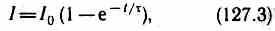
где I₀=ξ/R — установившийся ток (при t®¥)

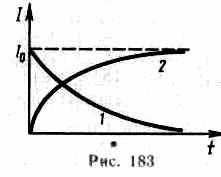
Таким образом, в процессе включения источника э.д.с. нарастание силы тока в цепи задается функцией (127.3) и опре­деляется кривой 2 на рис. 183. Сила тока возрастает от начального значения I=0 и асимптотически стремится к устано­вившемуся значению I₀=ξ/R. Скорость нарастания тока определяется тем же вре­менем релаксации t=L/R, что и убыва­ние тока. Установление тока происходит тем быстрее, чем меньше индуктивность цепи и больше ее сопротивление.

Оценим значение э.д.с. самоиндук­ции ξ_s, возникающей при мгновенном уве­личении сопротивления цепи постоянного тока от R₀ До R. Предположим, что мы размыкаем контур, когда в нем течет уста­новившийся ток I₀=ξ/R₀. При размыка­нии цепи ток изменяется по формуле (127.2). Подставив в нее выражение для I₀ и t, получим

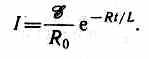
Э.д.с. самоиндукции

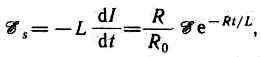
т. е. при значительном увеличении сопро­тивления цепи (R/R₀>>1) обладающей большой индуктивностью, э.д.с. самоин­дукции может во много раз превышать э.д.с. источника тока, включенного в цепь. Таким образом, необходимо учиты­вать, что контур, содержащий индуктив­ность, нельзя резко размыкать, так как это (возникновение значительных э.д.с. само­индукции) может привести к пробою изо­ляции и выводу из строя измерительных приборов. Если в контур сопротивление вводить постепенно, то э.д.с. самоиндук­ции не достигнет больших значений.