Свободные затухающие колебания– колебания, амплитуда которых из-за потерь энергии реальной колебательной системой с течением времени уменьшается. Простейшим механизмом уменьшения энергии колебаний является ее превращение в теплоту вследствие трения в механических колебательных системах, а также омических потерь и излучения электромагнитной энергии в электрических колебательных системах.
Дифференциальное уравнение свободных затухающих колебаний имеет вид
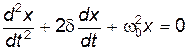 , (1)
, (1)
| где x – | колеблющаяся величина, описывающая тот или иной физический процесс; |
| d – | коэффициент затухания; |
| w0 – | циклическая частота собственных незатухающих колебаний (собственная частота колебательной системы). |
Решение уравнения (1) в случае малого затухания (d2 << 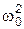 ) имеет вид
) имеет вид
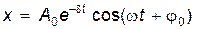 ,
,
где 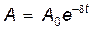 – –
| амплитуда затухающих колебаний; |
| A0 – | начальная амплитуда; |
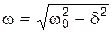 – –
| циклическая частота затухающих колебаний; |
| j0 – | начальная фаза колебаний. |
Промежуток времени 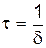 , в течение которого амплитуда уменьшается в e раз, называется временем релаксации.
, в течение которого амплитуда уменьшается в e раз, называется временем релаксации.
Затухание нарушает периодичность колебаний, поэтому затухающие колебания не являются периодическими. Однако, если затухание мало, то можно условно пользоваться понятием периода как промежутка времени между двумя следующими друг за другом максимумами (или минимумами) колеблющейся величины. Тогда период затухающих колебаний вычисляют по формуле
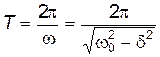 .
.
Если A(t) и A(t+T)– амплитуды двух последовательных колебаний, соответствующих моментам времени, отличающимся на период, то отношение
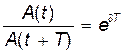
называется декрементом затухания, а его логарифм
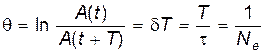 – логарифмическим декрементом затухания.
– логарифмическим декрементом затухания.
Величина Ne – это число колебаний, совершаемых за время уменьшения амплитуды в е раз. Логарифмический декремент затухания – постоянная величина для данной колебательной системы.
Для характеристики колебательной системы используют понятие добротности Q, которая при малых значениях логарифмического декремента равна
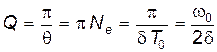 .
.
Добротность пропорциональна числу колебаний, совершаемых системой за время релаксации.
Вынужденные электрические колебания.

Переменные токи. Электрический резонанс.
Основные понятия волновых процессов: волна, типы волн, фронт волны, волновая поверхность. Плоские и сферические волны. Длина волны, фазовая скорость, волновое число.
Волна – процесс распространения колебаний в пространстве.
По природе:
-физические (механические, электромагнитные)
-химические
-биологические
Общим свойством всех волн любой природы является перенос Е без переноса вещества.
Линия, вдоль которой происходит перенос Е, называется лучем.
Частным случаем механических волн, являются упругие волны – это распространение деформации в упругих средах.
Упругая среда – это среда м/у частицами, м/у которыми существуют силы взаимодействия вызывающие упругую деформацию этой среды (твердые тела, жидкости, газы).
В вакууме, где достаточно сильно разряженные частицы и силы взаимодействия незначительны, механические волны не распространяются.
Колебания, возбужденные в какой-либо точке среды распространяются в ней со скоростью, зависящей от свойств среды (в частности от плотности среды), передавая возбуждение от одной точке среды к другой – max в твердых телах, min в газах.
По направлению смещения частиц среды различают волны:
-продольные
-поперечные
Продольные – волны, в которых колебания частиц происходят вдоль луча. Они м/т распространятся в средах, в результате возникновения упругих сил при деформации сжатия и растяжения (твердые, жидкие и газообразные тела).
Луч 
колебания частиц 
Поперечные – волны, колебания частиц которых происходят перпендикулярно лучу.
Они распространяются в средах, в которых возникают упругие силы при деформации сдвига (твердые тела)
 Луч
Луч 
При растяжении – длина волны увеличивается, при сжатии – уменьшается.
Таким образом, продольные волны во всех телах, поперечные только в твердых.
Дата: 2019-02-19, просмотров: 397.