Объяснение закона Фарадея в случае движущихся проводников.
Явление взаимной индукции. Взаимная индуктивность двух однослойных катушек, намотанных на общий сердечник.
Взаимная индукция — возникновение электродвижущей силы (ЭДС индукции) в одном проводнике вследствие изменения силы тока в другом проводнике или вследствие изменения взаимного расположения проводников.
Направление тока, возникшего при взаимоиндукции, определяется по правилу Ленца. Правило указывает на то, что изменение тока в одной цепи (катушке) встречает противодействие со стороны другой цепи (катушки).
Энергия магнитного поля.
Энергия магнитного поля показывает, какую работу затратил электрический ток в проводнике (катушке индуктивности) на создание этого магнитного поля. Естественно эта энергия будет напрямую зависеть от индуктивности проводника, вокруг которого магнитное поле создается.
Оказывается, энергия магнитного поля равна половине произведения индуктивности цепи на квадрат силы тока, т. е.

Сравнивая эту формулу с формулой для кинетической энергии, нетрудно убедиться в том, что они очень похожи одна на другую

Эта формула говорит нам о том, что кинетическая энергия прямо пропорциональна массе движущегося предмета и квадрату скорости его движения.
Все это не имеет, конечно, прямого отношения к электротехнике. Однако, мы уже несколько раз пользовались механическими аналогиями при рассмотрении электромагнитных явлений, сравнивая энергию магнитного поля с кинетической энергией, явление самоиндукции — с инерцией и, наконец, индуктивность с механической массой. Из сопоставления этих формул следует также, что силе тока в механике соответствует скорость движения.
Вихревое электрическое поле.
Ток смещения.

Уравнения Максвелла в интегральной и дифференциальной формах.



Квазиупругие колебания. Дифференциальное уравнение и его решение. Кинематические характеристики колебательного движения.
Превращение энергии при идеальных гармонических колебаниях.
Примеры квазиупругих колебаний: пружинный маятник, физический маятник, математический маятник.
Сложение однонаправленных колебаний одинаковы частоты. Метод векторных диаграмм.
Сложение колебаний с близкими частотами. Биения.
Затухающие колебания.
Затухающие колебания — это колебания, амплитуда которых уменьшается с течением времени под действием внешних сил.
Причина затухания заключается в том, что во всякой колебательной системе, кроме возвращающей силы, всегда действуют разного рода силы трения, сопротивление воздуха
и т. п., которые тормозят движение. При каждом размахе часть полной колебательной энергии (потенциальной и кинетической)расходуется на работу против сил трения. В конечном итоге на эту работу уходит весь запас энергии, сообщенный колебательной системе первоначально.
Рассматривая свободные гармонические колебания, мы имели дело с идеальными, строго периодическими собственными колебаниями. Описывая при помощи такой модели реальные колебания, мы сознательно допускаем неточность в описании. Однако подобное упрощение является пригодным в силу того, что у многих колебательных систем затухания колебаний, вызванные трением, действительно малы: система успевает совершить много колебаний прежде, чем их амплитуда уменьшится заметным образом.
Основные понятия волновых процессов: волна, типы волн, фронт волны, волновая поверхность. Плоские и сферические волны. Длина волны, фазовая скорость, волновое число.
Волна – процесс распространения колебаний в пространстве.
По природе:
-физические (механические, электромагнитные)
-химические
-биологические
Общим свойством всех волн любой природы является перенос Е без переноса вещества.
Линия, вдоль которой происходит перенос Е, называется лучем.
Частным случаем механических волн, являются упругие волны – это распространение деформации в упругих средах.
Упругая среда – это среда м/у частицами, м/у которыми существуют силы взаимодействия вызывающие упругую деформацию этой среды (твердые тела, жидкости, газы).
В вакууме, где достаточно сильно разряженные частицы и силы взаимодействия незначительны, механические волны не распространяются.
Колебания, возбужденные в какой-либо точке среды распространяются в ней со скоростью, зависящей от свойств среды (в частности от плотности среды), передавая возбуждение от одной точке среды к другой – max в твердых телах, min в газах.
По направлению смещения частиц среды различают волны:
-продольные
-поперечные
Продольные – волны, в которых колебания частиц происходят вдоль луча. Они м/т распространятся в средах, в результате возникновения упругих сил при деформации сжатия и растяжения (твердые, жидкие и газообразные тела).
Луч 
колебания частиц 
Поперечные – волны, колебания частиц которых происходят перпендикулярно лучу.
Они распространяются в средах, в которых возникают упругие силы при деформации сдвига (твердые тела)
 Луч
Луч 
При растяжении – длина волны увеличивается, при сжатии – уменьшается.
Таким образом, продольные волны во всех телах, поперечные только в твердых.
Волновое уравнение.
Распространение волн в однородной изотропной среде в общем случае описывается волновым уравнением - дифференциальным уравнением в частных производных.
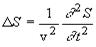 , (4) где
, (4) где 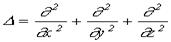 (5)-оператор Лапласа, v - фазовая скорость.
(5)-оператор Лапласа, v - фазовая скорость.
Решением уравнения (4) является уравнение любой волны (плоской, сферической и т.д.). В частности, для анализируемой здесь плоской гармонической волны (1), которая не зависит от координат y и z волновое уравнение принимает вид 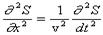 . (6)
. (6)
Cоответствующей подстановкой можно убедится, что уравнению (6) удовлетворяет уравнение (1).
Свойства волн.
Генерация волн. Волны могут генерироваться различными способами.
Генерация локализованным источником колебаний (излучателем, антенной).
Спонтанная генерация волн в объёме при возникновении гидродинамических неустойчивостей. Такую природу могут иметь, например,волны на водепри достаточно большой скоростиветра, дующего над водной гладью.
Переход волн одного типа в волны другого типа. Например, при распространении электромагнитных волнв кристаллическом твёрдом теле могут генерироватьсязвуковыеволны.
Как правило, волны способны удалиться сколь угодно далеко от генератора колебаний. По этому причине иногда волнами называют «колебание, оторвавшееся от излучателя». Исключение составляют так называемые температурные волны, амплитуда которых экспоненциально спадает при удалении от излучателя.
Распространение. Большинство волн, по своей природе, являются не настоящими новыми физическими сущностями, а лишь условным названием для определённого вида коллективного движения. Так, если в объёме газа возникла звуковая волна, то это не значит, что в этом объёме появились какие-то новые физические объекты.Звук— это лишь название для особого скоординированного типа движения тех же самых молекул. Т.е. большинство волн — это колебания некоторойсреды. Вне этой среды волны данного типа (например, звук в вакууме) не существуют.
Имеются, однако, волны, которые являются не «рябью» какой-либо иной среды, а представляют собой именно новые физические сущности. Так, электромагнитные волныв современной физике — это не колебание некоторой среды (называвшейся в XIX векеэфиром), а самостоятельное, самоподдерживающееся поле, способное распространяться в вакууме. Аналогично обстоит дело и с волнами вероятности материальных частиц.
Распространение волн — это, как правило, равномерный процесс, т.е. волны обычно распространяются с некоторой определённой скоростью(которая, конечно же, может зависеть от многих параметров).
При распространении в некоторой средеамплитудаволны может затухать, что связано сдиссипативнымипроцессами внутри среды, сквозь которую проходят волны. В случае некоторых специальным образом подготовленных метастабильных сред амплитуда волны могут, наоборот, усиливаться (пример: генерациялазерного излучения).
Взаимодействие с телами и границами раздела. Наиболее «спокойным» образом волна распространяется в однородной, однотипной среде. Если же на пути волны встречается какой-либо дефект среды, тело, или граница раздела двух сред, то это приводит к нарушению нормального распространения волны. Результат этого нарушения часто проявляется в виде следующих явлений:
Отражение, преломление, рассеяние, дифракция
Разумеется, конкретный вид законов, описывающих эти процессы, зависит от типа волны.
Пространственные размеры волны. Когда говорят опространственном размере волны, то имеют в виду размер той области пространства, где амплитуду колебания нельзя считать (в рамках рассматриваемой задачи) пренебрежимо малой. Большинство волн могут, теоретически, обладать сколь угодно большим размером, как в направлении движения, так и поперёк него. В реальности же все волны обладают конечными размерами. Продольный размер волны, как правило, определяется длительностью процесса излучения волны. Поперечный же размер определяется рядом параметров: размером излучателя, характером распространения волны (например, плоская, сферически расходящаяся волна и т.д.).
Некоторые виды волн, в частности, солитоны, являются ограниченными волнами по построению.
Волна ограниченного размера называется волновым пакетом, или цугом волн. В теории, волновой пакет описывается как сумма всевозможных плоских волн, взятых с определёнными весами. В случае нелинейных волн, форма огибающей волнового пакета эволюционирует с течением времени.
Поляризация. В каждой точке любой волны можно ввести некоторойвекторное поле. Так, если волна есть колебание некоторой среды, то этим вектором будет векторскоростичастицы этой среды в данной точке; если это электромагнитная волна, то этим вектором будетэлектрическое полеи т.д. Направление этого вектора задаёт поляризацию волны. Если этот вектор параллелен направлению движения волны (т.е. если среда колеблется вдоль направления движения), то волна называетсяпродольной. Если вектор перпендикулярен направлению движения волны (т.е. если среда колеблется поперёк направления движения), то волна называетсяпоперечной.
Поперечность или продольность волны определяется её природой. Так, например, плоские электромагнитные и гравитационные волны поперечны, звуковая волна в газе — продольна, а упругие волны в твёрдом теле могут быть как продольными, так и поперечными.
Фазовая когерентность.Когерентностьволны означает, что в различных точках волны осцилляции происходят синхронно, т.е. разность фаз между двумя точками не зависит от времени. Отсутствие когерентности, следовательно, это ситуация, когда разность фаз между двумя точками не константа, а почти случайно «скачет» со временем (сбои фаз). Такая ситуация может иметь место, если волна была сгенерирована не единым излучателем, а совокупностью одинаковых, но независимых (т.е. нескорелированных) излучателей.
Изучение когерентности световых волн приводит к понятиям временнойипространственной когерентности. При распространении электромагнитных волн вволноводахмогут иметь местофазовые сингулярности. В случае волн на воде когерентность волны определяет так называемаявторая периодичность.
Скорость звука в газах.
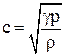 ,
,
где p – давление газа, не возмущенного волной;
r – плотность газа, не возмущенного волной;
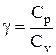 – отношение молярной теплоемкости газа при постоянном давлении к теплоемкости газа при постоянном объеме.
– отношение молярной теплоемкости газа при постоянном давлении к теплоемкости газа при постоянном объеме.
Амплитуда звукового давления Dp0 и амплитуда скорости v0 частиц в звуковой волне связаны соотношением
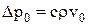 .
.
Интенсивность звука I, выраженная через амплитуду звукового давления – энергия, переносимая звуковой волной за единицу времени через единичную площадку, перпендикулярную направлению распространения волны:
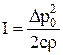 ,
,
где r – плотность газа.
Уровень интенсивности звука (в децибелах) определяется формулой
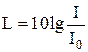 ,
,
где I – интенсивность данного звука;
I0 = 10–12 Вт/м2 – интенсивность звука на пороге слышимости при стандартной частоте n = 1 кГц.
Уровень громкости звука (в фонах) вычисляется по формуле
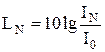 ,
,
где IN – интенсивность звука стандартной частоты n = 1 кГц, равногромкого с исследуемым звуком.
Явление Доплера – если источник и приемник звука перемещаются относительно среды, в которой распространяется звук, то частота звуковых колебаний n', регистрируемая приемником звука, связана с частотой собственных колебаний n источника соотношением
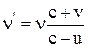 ,
,
где c, u, v – скорости соответственно звука, его источника и приемника.
Примечание. Записанная формула относится к случаю, если источник и приемник звука движутся по одной прямой. При этом величины u, v – алгебраические: u > 0, если источник движется к приемнику; u < 0, если источник удаляется от приемника. Аналогично v > 0, если приемник приближается к источнику; v < 0, если приемник движется от источника.
Вектор плотности потока энергии волны – физическая величина, модуль которой равен энергии DW, переносимой волной за единицу времени (Dt = 1) через единичную площадку, расположенную перпендикулярно направлению распространения волны (DS^):
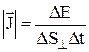 ;
; 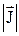 = u v; J = u×v,
= u v; J = u×v,
где u – плотность энергии в каждой точке среды, среднее значение которой вычисляется по формуле 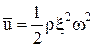 ;
;
ρ – плотность среды;
x0 – амплитуда волны;
w – круговая (циклическая частота);
v – фазовая скорость (скорость перемещения фазы волны).
Энергия, работа, мощность. Законы
сохранения в механике
Энергия – количественная мера и качественная характеристика движения и взаимодействия материи во всех ее превращениях. Она является функцией состояния системы и характеризует способности системы к совершению работы при переходе из одного состояния в другое.
Изменение энергии при переходе системы из одного состояния в другое равно работе, совершаемой системой в процессе перехода:
DW = W1 – W2 = A.
Диссипация (рассеяние) энергии механических систем –процесс перехода части их механической энергии в другие формы под влиянием внешних факторов (например, за счет наличия сил сопротивления).
Диссипативные системы – системы, в которых полная механическая энергия постепенно уменьшается за счет преобразования в другие (немеханические) формы, например в теплоту.
Механическая энергия – физическая величина, равная работе, которая может быть произведена при полном превращении движения данной формы в механическую форму движения материи.
Кинетическая энергия - физическая величина, характеризующая способность движущегося тела или системы совершать работу при торможении до полной остановки – одна из функций состояния ее движения:
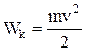 .
.
Кинетическая энергия системы – сумма кинетических энергий отдельных тел (материальных точек) этой системы:
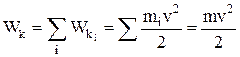 ,
,
где 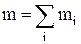 – масса тела (системы);
– масса тела (системы);
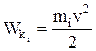 – кинетическая энергия i-го тела системы.
– кинетическая энергия i-го тела системы.
Связь между кинетической энергией тела (системы) и его импульсом:
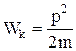 .
.
Кинетическая энергия при вращательном движении:
1) элементарной массы Dmi:
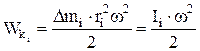 ,
,
где Ii = Dmi∙ri2 – момент инерции материальной точки, относительно выбранной оси вращения;
2) тела (системы):
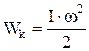 ,
,
где 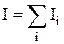 – момент инерции тела относительно той же оси вращения.
– момент инерции тела относительно той же оси вращения.
Потенциальная энергия–физическая величина, характеризующая способность системы совершать работу, связанную с изменением конфигурации и взаимного расположения тел или частей в системе.
Изменение потенциальной энергии системы зависит только от начального и конечного ее состояний и равно работе внутренних (консервативных) сил системы, взятой с обратным знаком:
dWp = –dA.
Характеристики поля тяготения – напряженность и потенциал поля тяготения.
Напряженностью поля тяготения в данной точке называется векторная физическая величина, равная по величине и направлению силе, действующей на единичную массу, помещенную в данную точку поля:
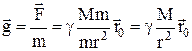 .
.
Потенциалом поля тяготения называют скалярную физическую величину, равную потенциальной энергии единичной массы, помещенной в данную точку поля:
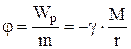 ,
,
т.е. потенциал поля тяготения тоже с увеличением расстояния увеличивается и при r ® ¥ равен нулю.
Связь между напряженностью и потенциалом поля тяготения:
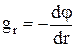 .
.
Условие максимума
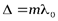 :
: 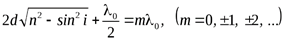 (8)
(8)
Условие минимума
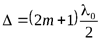 :
: 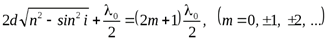 (9)
(9)
При освещении пленки белым светом она окрашивается в какой-либо определенный цвет, длина волны которого удовлетворяет максимуму интерференции. Следовательно, по цвету пленки можно оценивать её толщину.
Условия (8), (9) зависят при постоянных значениях n, l0 от угла падения i и толщины пленки d, в зависимости от этого различают полосы равного наклона и полосы равной толщины.
Полосами равного наклона называют интерференционные полосы, возникающие в результате наложения лучей, падающих на плоскопараллельную пластинку под одинаковыми углами.
Полосами равной толщины называют интерференционные полосы, возникающие в результате наложения лучей, падающих на пластинку переменной толщины от мест одинаковой толщины.
Кольца Ньютона
 Кольца Ньютона - классический пример полос равной толщины.
Кольца Ньютона - классический пример полос равной толщины.
В отраженном свете оптическая разность хода (с учетом потери полуволны λ0/2 при отражении от плоскопараллельной пластинки):
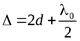 , (10)
, (10)
где d – ширина зазора.
R2 = r2 + (R – d)2 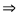
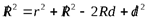
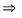 (d << R)
(d << R) 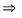
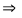
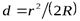 .
.
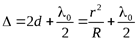 . (11)
. (11)
Условие максимума 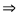 радиус светлого кольца
радиус светлого кольца
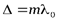 :
: 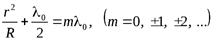
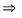
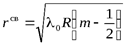 (12)
(12)
Условие минимума 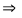 радиус темного кольца
радиус темного кольца
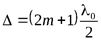 :
: 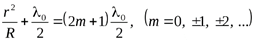
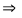
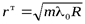 (13)
(13)
Система светлых и темных полос получается только при освещении монохроматическим светом. В белом свете интерференционная картина изменяется, - каждая светлая полоса превращается в спектр.
Кольца Ньютона можно наблюдать и в проходящем свете. При этом максимумы интерференции в отраженном свете соответствуют минимумам в проходящем и наоборот.
Измеряя радиусы колец Ньютона, можно определить λ0 (зная радиус кривизны линзы R ) или R (зная λ0 ).
Принцип Гюйгенса-Френеля
Световая волна, возбуждаемая каким-либо источником света, может быть представлена как результат суперпозиции когерентных вторичных волн, «излучаемых» фиктивными источниками.
Дифракционные явления присущи всем волновым процессам, но особенно отчетливо проявляются лишь в тех случаях, когда длины волн излучений сопоставимы с размерами препятствий. Так, звуковые волны хорошо слышны за углом дома, т.е. звуковая волна его огибает. Для наблюдения же дифракции световых волн необходимо создание специальных условий. Это обусловлено малостью длин световых волн (λ<1мкм).
Условия наблюдения дифракции 3Дифракция происходит на предметах любых размеров, а не только соизмеримых с длиной волны l Условия наблюдения дифракции 3Трудности наблюдения заключаются в том, что вследствие малости длины световой волны интерференционные максимумы располагаются очень близко друг к другу, а их интенсивность быстро убывает Дифракция от различных препятствий: а) от тонкой проволочки; б) от круглого отверстия; в) от круглого непрозрачного экрана.
Квантовый характер излучения. Формула Планка. Следствия из формулы Планка.
Для получения правильного вида 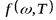 немецкий физик Макс Планк в 1900 году сформулировалквантовую гипотезу, согласно которой электромагнитное излучение испускается в виде отдельных порций энергии квантов, величина которых пропорциональна частоте излучения:
немецкий физик Макс Планк в 1900 году сформулировалквантовую гипотезу, согласно которой электромагнитное излучение испускается в виде отдельных порций энергии квантов, величина которых пропорциональна частоте излучения:
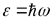 .
.
Константа 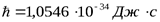 называется постоянной Планка. Из гипотезы Планка может быть получено следующее выражение для средней энергии излучения с частотой
называется постоянной Планка. Из гипотезы Планка может быть получено следующее выражение для средней энергии излучения с частотой 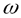 :
:
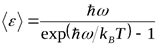 ,
,
что существенно отличается от 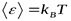 в классической теории.
в классической теории.
Для универсальной функции Кирхгофа находим:
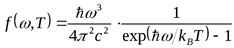 .
.
Соотношение называют формулой Планка. В области низких частот 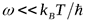 (2.3) переходит в формулу Рэлея-Джинса. В области высоких частот
(2.3) переходит в формулу Рэлея-Джинса. В области высоких частот 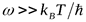 из (2.3) находим:
из (2.3) находим:
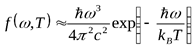 ,
,
что хорошо согласуется с результатами эксперимента.
С ростом температуры максимум функции 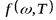 смещается в область более высоких частот,
смещается в область более высоких частот, 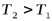 .
.
Для энергетической светимости абсолютно черного тела получается выражение:
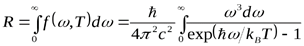 .
.
Выполним замену переменной 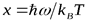 :
:
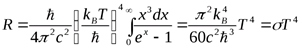 .
.
Константа 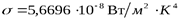 называется постоянной Стефана-Больцмана, а соотношение
называется постоянной Стефана-Больцмана, а соотношение 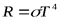 -законом Стефана-Больцмана.
-законом Стефана-Больцмана.
Вычисляя производную 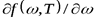 и приравнивая ее нулю, находим, что максимум излучательной способности абсолютно черного тела приходится на длину волны:
и приравнивая ее нулю, находим, что максимум излучательной способности абсолютно черного тела приходится на длину волны:
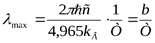 .
.
Видно, что с ростом температуры 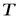 , максимум излучательной способности смещается в сторону более коротких волн. Соотношение называютзаконом смещения Вина.
, максимум излучательной способности смещается в сторону более коротких волн. Соотношение называютзаконом смещения Вина.
Эффект Комптона.

 В 1923 году американский физик А. Комптон, исследуя рассеяние монохроматических рентгеновских лучей веществами с легкими атомами (парафином, бором и др.), обнаружил, что в составе рассеянного излучения наряду с излучением первоначальной длины волны наблюдается также излучение более длинных волн.
В 1923 году американский физик А. Комптон, исследуя рассеяние монохроматических рентгеновских лучей веществами с легкими атомами (парафином, бором и др.), обнаружил, что в составе рассеянного излучения наряду с излучением первоначальной длины волны наблюдается также излучение более длинных волн.
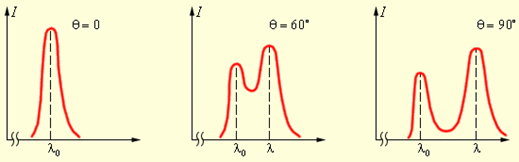
Рис. 12. Спектры рассеянного излучения.
Эффектом Комптона называется упругое рассеяние коротковолнового электромагнитного излучения (рентгеновского и g-излучения) на свободных или слабо связанных электронах вещества, сопровождающееся увеличением длины волны.
Эффект Комптона не укладывается в рамки волновой теории, согласно которой длина волны излучения не должна изменяться при рассеянии.
Пусть на покоящийся электрон с массой m и энергией покоя m0c2 падает рентгеновский фотон с энергией hn. В результате упругого столкновения электрон приобретает импульс, равный 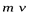 , и его полная энергия становится равнойmc2. Фотон, столкнувшись с электроном, передает ему часть своей энергии и импульса и изменяет направление движения (рассеивается) на угол q.
, и его полная энергия становится равнойmc2. Фотон, столкнувшись с электроном, передает ему часть своей энергии и импульса и изменяет направление движения (рассеивается) на угол q.
pe=mv
p¢ф= hn¢/c
 pф=hn/c
pф=hn/c
 q
q
Закон сохранения энергии
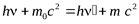 (12)
(12)
Закон сохранения импульса
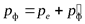 (13)
(13)

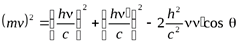 (14)
(14)
(12) 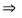
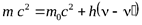
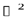
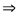
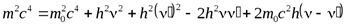 (15)
(15)
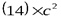
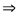
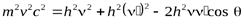 (16)
(16)
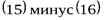
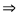
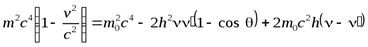
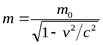
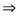
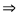
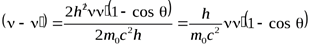
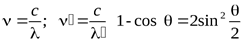
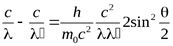
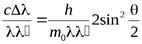
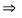
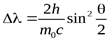 -формула Комптона, (17)
-формула Комптона, (17)
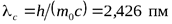 -комптоновская длина волны электрона.
-комптоновская длина волны электрона.
Эффект Комптона наблюдается не только на электронах, но и на других заряженных частицах, например, протонах. Однако ввиду большой массы протона его отдача ощущается лишь при рассеянии фотонов очень больших энергий.
Модель атома Томсона.
В 1904 году появились публикации о строении атома, одни из которых принадлежали японскому физику Хантаро Нагаока, другие - английскому физику Д.Д. Томсону.
Нагаока представил строение атома аналогичным строению солнечной системы: роль Солнца играет положительно заряженная центральная часть атома, вокруг которой по установленным кольцеобразным орбитам движутся “планеты” - электроны. При незначительных смещениях электроны возбуждают электромагнитные волны.
Дж.Томсон стремился найти модель, которая позволила бы объяснить все его известные свойства. Поскольку преобладающая доля массы атома сосредоточена в его положительно заряженной части, он принял, что атом представляет собой сферическое распределение положительного заряда радиусом примерно 10–10 м, а на его поверхности находятся электроны, удерживаемые упругими силами, позволяющими им колебаться (рис. 4). Суммарный отрицательный заряд электронов в точности компенсирует положительный заряд, так что атом электрически нейтрален. В простейшем атоме водорода электрон находится в центре положительно заряженной сферы. В многоэлектронных атомах электроны располагаются по устойчивым конфигурациям, рассчитанным Томсоном. Томсон считал каждую такую конфигурацию определяющей химические свойства атомов. Электроны находятся на сфере, но могут совершать простые гармонические колебания относительно положения равновесия. Такие колебания могут происходить лишь с определенными частотами, которым соответствуют узкие спектральные линии, наблюдающиеся в газоразрядных трубках. Электроны можно довольно легко выбить с их позиций, в результате чего возникают положительно заряженные «ионы», из которых состоят «каналовые лучи» в опытах с масс-спектрографом. X-лучи соответствуют очень высоким обертонам основных колебаний электронов. Альфа-частицы, возникающие при радиоактивных превращениях, – это часть положительной сферы, выбитая из нее в результате какого-то энергичного разрывания атома.
о вскоре оказалось, что новые опытные факты опровергают модель Томсона и, наоборот, свидетельствуют в пользу планетарной модели. Эти факты были открыты Резерфордом. В первую очередь следует отметить открытие ядерного строения атома.
Резерфорд заметил, что быстродвижущиеся альфа-частицы способны проходить сквозь тонкую золотую фольгу, не оставляя видимых следов, но при этом слегка отклоняются. Возникло предположение, что атомы золота, твердые, непроницаемые, как "крошечные бильярдные шары" - как ранее считали ученые, - были мягкими внутри! Все выглядело так, будто меньшие и более твердые альфа-частицы могут проходить сквозь атомы золота как высокоскоростная пуля через желе.
В 1909-1911гг. Резерфорд применил зондирование атома с помощью α-частиц, которые возникают при радиоактивном распаде радия и некоторых других элементов. Масса α-частиц приблизительно в 7300 раз больше массы электрона, а положительный заряд равен удвоенному элементарному заряду. В своих опытах Резерфорд использовал α-частицы с кинетической энергией около 5 МэВ (скорость таких частиц очень велика – порядка 107м/с, но она все же значительно меньше скорости света). α-частицы – это полностью ионизированные атомы гелия. Они были открыты Резерфордом в 1899 году. Этими частицами Резерфорд бомбардировал атомы тяжелых элементов (золото, серебро, медь и др.). Электроны, входящие в состав атомов, вследствие малой массы не могут заметно изменить траекторию α-частицы. Рассеяние, то есть изменение направления движения α-частиц, может вызвать только тяжелая положительно заряженная часть атома. Схема опыта Резерфорда представлена на рис. 2.
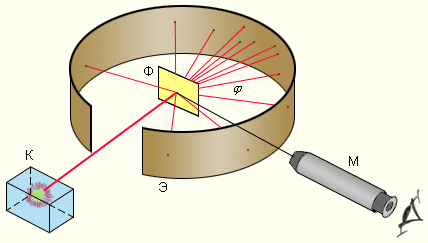
|
| Рисунок 2. Схема опыта Резерфорда по рассеянию α-частиц. K – свинцовый контейнер с радиоактивным веществом, Э – экран, покрытый сернистым цинком, Ф – золотая фольга, M – микроскоп. |
От радиоактивного источника, заключенного в свинцовый контейнер, α-частицы направлялись на тонкую металлическую фольгу. Рассеянные частицы попадали на экран, покрытый слоем кристаллов сульфида цинка, способных светиться под ударами быстрых заряженных частиц. Сцинтилляции (вспышки) на экране наблюдались глазом с помощью микроскопа. Наблюдения рассеянных α-частиц в опыте Резерфорда можно было проводить под различными углами φ к первоначальному направлению пучка. Было обнаружено, что большинство α-частиц проходит через тонкий слой металла, практически не испытывая отклонения. Однако небольшая часть частиц отклоняется на значительные углы, превышающие 30°. Очень редкие α-частицы (приблизительно одна на десять тысяч) испытывали отклонение на углы, близкие к 180°. Но Резерфорд обнаружил, что некоторые α-частицы, проходя сквозь золотую фольгу, отклоняются очень сильно. Фактически некоторые вообще отлетают назад! Почувствовав, что за этим кроется нечто важное, ученый тщательно посчитал количество частиц, полетевших в каждом направлении. Затем путем сложного, но вполне убедительного математического анализа он показал единственный путь, которым можно было объяснить результаты экспериментов: атом золота состоял почти полностью из пустого пространства, а практически вся атомная масса была сконцентрирована в центре, в маленьком "ядре" атома!
Этот результат был совершенно неожиданным даже для Резерфорда. Он находился в резком противоречии с моделью атома Томсона, согласно которой положительный заряд распределен по всему объему атома. При таком распределении положительный заряд не может создать сильное электрическое поле, способное отбросить α-частицы назад. Электрическое поле однородного заряженного шара максимально на его поверхности и убывает до нуля по мере приближения к центру шара. Если бы радиус шара, в котором сосредоточен весь положительный заряд атома, уменьшился в nраз, то максимальная сила отталкивания, действующая на α-частицу возросла бы вn2раз. Следовательно, при достаточно большом значенииnα-частицы могли бы испытать рассеяние на большие углы вплоть до 180°. Эти соображения привели Резерфорда к выводу, что атом почти пустой, и весь его положительный заряд сосредоточен в малом объеме. Эту часть атома Резерфорд назвалатомным ядром. Так возниклаядерная модельатома. Рис. 3 иллюстрирует рассеяние α-частицы в атоме Томсона и в атоме Резерфорда.
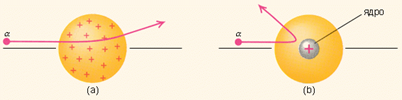
|
| Рисунок 3. Рассеяние α-частицы в атоме Томсона (a) и в атоме Резерфорда (b). |
Таким образом, опыты Резерфорда и его сотрудников привели к выводу, что в центре атома находится плотное положительно заряженное ядро, диаметр которого не превышает 10–14–10–15м. Это ядро занимает только 10–12часть полного объема атома, но содержитвесьположительный заряд и не менее 99,95 % его массы. Веществу, составляющему ядро атома, следовало приписать колоссальную плотность порядка ρ ≈ 1015г/см3. Заряд ядра должен быть равен суммарному заряду всех электронов, входящих в состав атома. Впоследствии удалось установить, что если заряд электрона принять за единицу, то заряд ядра в точности равен номеру данного элемента в таблице Менделеева.
Опираясь на классические представления о движении микрочастиц, Резерфорд предложил планетарную модель атома. Согласно этой модели, в центре атома располагается положительно заряженное ядро, в котором сосредоточена почти вся масса атома.Атом в целом нейтрален. Вокруг ядра, подобно планетам, вращаются под действием кулоновских сил со стороны ядра электроны (рис. 4). Находиться в состоянии покоя электроны не могут, так как они упали бы на ядро.
Планетарная модель атома, предложенная Резерфордом, несомненно, явилась крупным шагом в развитии знаний о строении атома. Она была совершенно необходимой для объяснения опытов по рассеянию α-частиц. Однако она оказалась неспособной объяснить сам факт длительного существования атома, т. е. его устойчивость. По законам классической электродинамики, движущийся с ускорением заряд должен излучать электромагнитные волны, уносящие энергию. За короткое время (порядка 10–8с) все электроны в атоме Резерфорда должны растратить всю свою энергию и упасть на ядро. То, что этого не происходит в устойчивых состояниях атома, показывает, что внутренние процессы в атоме не подчиняются классическим законам.
Таким образом, изучение рассеяния α- частиц положило начало развитию именно ядерной теории атома, так как планетарная модель Резерфорда оказалась несостоятельной. К 20-м годам XX века физики уже не сомневались в том, что атомные ядра, открытые в 1911 г., также как и сами атомы, имеют сложную структуру. В этом их убеждали многочисленные экспериментальные факты, накопленные к этому времени: открытие радиоактивности, экспериментальное доказательство ядерной модели ядра, открытие искусственной радиоактивности и ядерных реакций, измерение зарядов атомных ядер и т. д. В настоящее время твердо установлено, что атомные ядра различных элементов состоят из двух частиц –протонов и нейтронов. Первая из этих частиц представляет собой атом водорода, из которого удален единственный электрон. Эта частица наблюдалась уже в опытах Томсона 1907 г.. В 1919 году Э. Резерфорд обнаружил ядра атома водорода в продуктах расщепления ядер атомов многих элементов. Резерфорд назвал эту частицу протоном. Он высказал предположение, что протоны входят в состав всех атомных ядер. Схема опытов Резерфорда представлена на рис. 5.
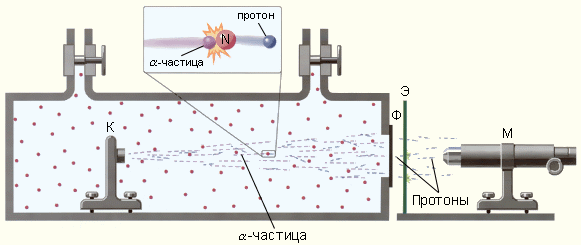
|
| Рисунок 5. Схема опытов Резерфорда по обнаружению протонов в продуктах расщепления ядер. К – свинцовый контейнер с радиоактивным источником α-частиц, Ф – металлическая фольга, Э – экран, покрытый сульфидом цинка, М – микроскоп. |
Прибор Резерфорда состоял из вакуумированной камеры, в которой был расположен контейнер (К) с источником α-частиц. Окно камеры было закрыто металлической фольгой (Ф), толщина которой была подобрана так, чтобы α-частицы не могли через нее проникнуть. За окном располагался экран (Э), покрытый сернистым цинком. С помощью микроскопа (М) можно было наблюдать сцинтилляции в точках попадания на экран тяжелых заряженных частиц. При заполнении камеры азотом при низком давлении на экране возникали световые вспышки, указывающие на появление потока каких-то частиц, способных проникать через фольгу (Ф), практически полностью задерживающую поток α-частиц. Отодвигая экран (Э) от окна камеры, Резерфорд измерил среднюю длину свободного пробеганаблюдаемых частиц в воздухе. Она оказалась приблизительно равной 28 см, что совпадало с оценкой длины пробега H-частиц, наблюдавшихся ранее Дж. Томсоном. Исследования действия на частицы, выбиваемые из ядер азота, электрических и магнитных полей показали, что эти частицы обладают положительным элементарным зарядом и их масса равна массе ядра атома водорода. Впоследствии опыт был выполнен с целым рядом других газообразных веществ. Во всех случаях было обнаружено, что из ядер этих веществ α-частицы выбивают H-частицы или протоны.
По современным измерениям, положительный заряд протона в точности равен e = 1,60217733·10–19Кл, то есть, равен по модулю отрицательному заряду электрона. В настоящее время равенство зарядов протона и электрона проверено с точностью 10–22. Такое совпадение зарядов двух непохожих друг на друга частиц вызывает удивление и остается одной из фундаментальных загадок современной физики.Масса протона, по современным измерениям, равнаmp= 1,67262·10–27кг.
Таким образом, в опыте Резерфорда было открыто явление расщепления ядер азота и других элементов при ударах быстрых α-частиц и показано, что протоны входят в состав ядер атомов.
После открытия протона было высказано предположение, что ядра атомов состоят из одних протонов. Однако это предположение оказалось несостоятельным, так как отношение заряда ядра к его массе не остается постоянным для разных ядер, как это было бы, если бы в состав ядер входили одни протоны. Для более тяжелых ядер это отношение оказывается меньше, чем для легких, т. е. при переходе к более тяжелым ядрам масса ядра растет быстрее, чем заряд.
В 1920 г. Резерфорд высказал гипотезу о существовании в составе ядер жестко связанной компактной протон-электронной пары, представляющей собой электрически нейтральное образование – частицу с массой, приблизительно равной массе протона. Он даже придумал название этой гипотетической частице – нейтрон. Это была очень красивая, но, как выяснилось впоследствии, ошибочная идея. Электрон не может входить в состав ядра.
Идея о существовании тяжелой нейтральной частицы казалась Резерфорду настолько привлекательной, что он незамедлительно предложил группе своих учеников во главе с Дж. Чедвикомзаняться поиском такой частицы. Через 12 лет в 1932 г. Чедвик экспериментально исследовал излучение, возникающее при облучении бериллия α-частицами, и обнаружил, что это излучение представляет собой поток нейтральных частиц с массой, примерно равной массе протона. Так был открытнейтрон.На рис. 6. приведена упрощенная схема установки для обнаружения нейтронов.
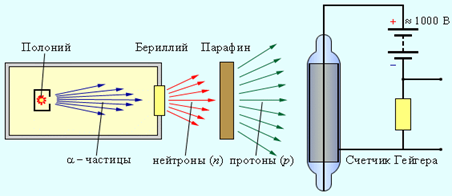
|
| Рисунок 6. Схема установки для обнаружения нейтронов. |
При бомбардировке бериллия α-частицами, испускаемыми радиоактивным полонием, возникает сильное проникающее излучение, способное преодолеть такую преграду, как слой свинца толщиной в 10–20 см. Это излучение почти одновременно с Чедвиком наблюдали супруги Жолио-Кюри Ирен и Фредерик (Ирен – дочь Марии и Пьера Кюри), но они предположили, что это γ-лучи большой энергии. Они обнаружили, что если на пути излучения бериллия поставить парафиновую пластину, то ионизирующая способность этого излучения резко возрастает. Они доказали, что излучение бериллия выбивает из парафина протоны, которые в большом количестве имеются в этом водородосодержащем веществе. По длине свободного пробега протонов в воздухе они оценили энергию γ-квантов, способных при столкновении сообщить протонам необходимую скорость. Она оказалась огромной – порядка 50 МэВ.
Дж. Чедвик в 1932 г. выполнил серию экспериментов по всестороннему изучению свойств излучения, возникающего при облучении бериллия α-частицами. В своих опытах Чедвик использовал различные методы исследования ионизирующих излучений. Счетчик Гейгера, предназначенный для регистрации заряженных частиц. Он состоит из стеклянной трубки, покрытой изнутри металлическим слоем (катод), и тонкой нити, идущей вдоль оси трубки (анод). Трубка заполняется инертным газом (обычно аргоном) при низком давлении. Заряженная частица, пролетая в газе, вызывает ионизацию молекул. Появившиеся в результате ионизации свободные электроны ускоряются электрическим полем между анодом и катодом до энергий, при которых начинается ударная ионизация. Возникает лавина ионов, и через счетчик проходит короткий разрядный импульс тока. Другим важнейшим прибором для исследования частиц является так называемаякамера Вильсона, в которой быстрая заряженная частица оставляет след (трек). Траекторию частицы можно наблюдать непосредственно или фотографировать. Действие камеры Вильсона, созданной в 1912 г., основано на конденсации перенасыщенного пара на ионах, образующихся в рабочем объеме камеры вдоль траектории, заряженной частицы. С помощью камеры Вильсона можно наблюдать искривление траектории заряженной частицы в электрическом и магнитном полях.
Дж. Чедвик в своих опытах наблюдал в камере Вильсона треки ядер азота, испытавших столкновение с бериллиевым излучением. На основании этих опытов он сделал оценку энергии γ-кванта, способного сообщить ядрам азота наблюдаемую в эксперименте скорость. Она оказалась равной 100–150 МэВ. Такой огромной энергией не могли обладать γ-кванты, испущенные бериллием. На этом основании Чедвик заключил, что из бериллия под действием α-частиц вылетают не безмассовые γ-кванты, а достаточно тяжелые частицы. Поскольку эти частицы обладали большой проникающей способностью и непосредственно не ионизировали газ в счетчике Гейгера, следовательно, они были электронейтральны. Так было доказано существование нейтрона – частицы, предсказанной Резерфордом более чем за 10 лет до опытов Чедвика.
Нейтрон – это элементарная частица. Ее не следует представлять в виде компактной протон-электронной пары, как первоначально предполагал Резерфорд.
По современным измерениям, масса нейтрона mn= 1,67493·10–27кг = 1,008665 а. е. м. Масса нейтрона приблизительно на две электронные массы превосходит массу протона.
Также, важным следствием теории Резерфорда было указание на заряд атомного центра, который Резерфорд положил равным ±Ne. Заряд оказался пропорциональным атомному весу. "Точное значение заряда центрального ядра не было определено, писал Резерфорд, - но для атома золота оно приблизительно равно 100 единицам заряда". Из последующих исследований и экспериментов Гейгера и Мардсена, предпринявших проверку формул Резерфорда, возникло представление о ядре как устойчивой части атома, несущей в себе почти всю массу атома и обладающей положительным (Резерфорд считал знак заряда неопределенным) зарядом. При этом число элементарных зарядов оказалось пропорциональным атомному весу. Заряд ядра оказался важнейшей характеристикой атома. В 1913 году было показано, что заряд ядра совпадает с номером элемента в таблице Менделеева. Бор писал: "С самого начала было ясно, что благодаря большой массе ядра и его малой протяженности в пространстве сравнительно с размерами всего атома строение электронной системы должно зависеть почти исключительно от полного электрического заряда ядра. Такие рассуждения сразу наводили на мысль о том, что вся совокупность физических и химических свойств каждого элемента может определяться одним целым числом..." После знакомства с Резерфордом Бор, отказавшись от изучения электронной модели, начал работу в его группе. Обратившись к планетарной модели, Бор создал на ее основе теорию атома Резерфорда-Бора.
Резерфорд понял революционный характер идей Бора и обсудил с ним основы этой теории, высказал критические замечания, после чего статьи Бора были опубликованы. Открытие Резерфордом атомных ядер является основой всех современных теорий строения атома. Когда Нильс Бор через два года опубликовал знаменитый труд, описывающий атом как миниатюрную солнечную систему, управляемую квантовой механикой, он использовал для своей модели в качестве отправной точки ядерную теорию Резерфорда. Так же поступили Гейзенберг и Шрёдингер, когда они сконструировали более сложные атомные модели, используя классическую и волновую механику.
Итак , как мы уже говорили Планетарная модель атома – это попытка применения классических представлений о движении тел к явлениям атомных масштабов. Эта попытка оказалась несостоятельной. Классический атом неустойчив. Электроны, движущиеся по орбите с ускорением, должны неизбежно упасть на ядро, растратив всю энергию на излучение электромагнитных волн.
Волновая функция
Для описания вероятности нахождения частицы в данный момент времени в некоторой точке пространства вводят волновую функцию (амплитуду вероятности) y(х, у, z, t).
Поэтому вероятность dw того, что частица находится в элементе объема dV, пропорциональна |y|2, т. е.
dw = |y|2dV
или
dw = |y|2dxdydz. (4.7)
Физический смысл имеет не сама волновая функция y(х, у, z, t), а квадрат ее модуля
|y|2 = yy*,
где y* - функция, комплексно сопряженная с y, т. е. величина |y|2 имеет смысл плотности вероятности
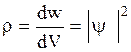 , (4.8)
, (4.8)
которая определяет вероятность появления частицы в данной точке пространства.
Следовательно, |y|2 определяет интенсивность волн де Бройля.
Пребывание частицы, где-либо в пространстве - достоверное событие и его вероятность равна единице, т. е. должно выполняться условие нормировки
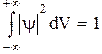 . (4.9)
. (4.9)
Вывод: Волновая функция (амплитуда вероятности) y(х, у, z, t) является основной характеристикой состояния квантовой системы.
Движение любой квантовой частицы можно описать волновым уравнением. Статистическое истолкование волн де Бройля и соотношений неопределенностей Гейзенберга указывают на то, что уравнение движения частицы в квантовой механике должно быть таким, чтобы оно позволяло объяснить наблюдаемые на опыте волновые свойства частиц.
Состояние частицы в данный момент времени в пространстве определяется в квантовой механике заданием волновой функции y(х, у, z, t), точнее величиной |y|2, определяющей вероятность нахождения частицы в некоторой точке с координатами х, у, z в данный момент времени t.
Поэтому основное уравнение квантовой механики должно быть уравнением относительно волновой функции (х, у, z, t) и играть роль волнового уравнения, решения которого позволяли бы объяснить эксперименты, например, по дифракции микрочастиц, указывающих на их волновые свойства.
Следует отметить, что процессе экспериментов выявился факт взаимодействия микрочастицы с измерительным прибором, т. е. сам человек, проводящий эксперимент влияет на результат опыта.
АТОМНОГО ЯДРА
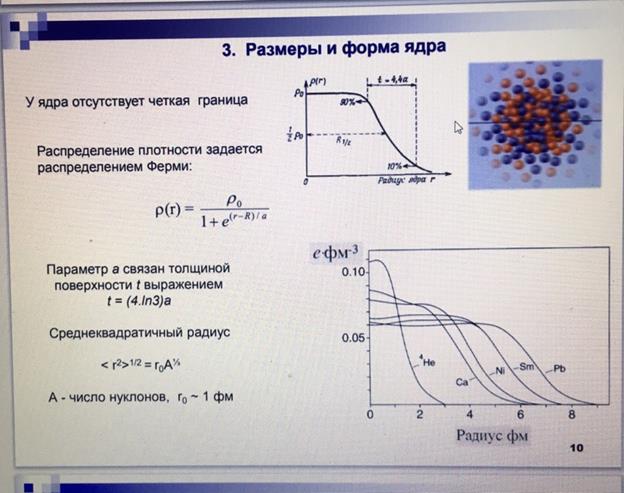
Ядром называется центральная часть атома, в которой сосредоточена практически вся масса и его положительный заряд.
Атомное ядро было открыто Резерфордом (1911 г.) в экспериментах по рассеиванию a - частиц веществом.
В 1932г. Иваненко и Гейзенберг создали протонно-нейтронную модель ядра. Согласно этой модели в состав ядра входят протоны и нейтроны. Протоны и нейтроны считаются двумя различными зарядовыми состояниями одной частицы – нуклона.
В ядерной физике принято выражать массу в единицах энергии (обычно в мегаэлектронвольтах, сокращенно МэВ). В основе этого лежит закон эквивалентности массы и энергии:
E=mc2
Применяется также другая единица – атомная единица массы (сокращенно а.е.м.); 1 а.е.м. эквивалентна 931,5 МэВ.
Характеристики нуклонов
Протон. Обозначается буквой p. Обладает электрическим зарядом +e; масса протона mР = 938,28 МэВ. Масса электрона (для сравнения) равна mе = 0,511 МэВ. Таким образом,
mР = 1836 me
Протон имеет полуцелый спин Sp = 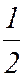 и собственный магнитный момент.
и собственный магнитный момент.
Нейтрон (n). Был открыт Чедвиком (1932 г.). Электрический заряд нейтрона равен нулю. Масса нейтрона mn = 939,57 МэВ и превышает массу протона приблизительно на 2,5 массы электрона (mn – mр 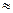 2,5mе). Нейтрон имеет полуцелый спин Sn =
2,5mе). Нейтрон имеет полуцелый спин Sn = 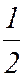 и собственный магнитный момент .
и собственный магнитный момент .
В свободном состоянии нейтрон нестабилен и распадается по схеме: ~
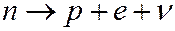 (3)
(3)
Период полураспада 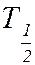 составляет приблизительно 12 минут.
составляет приблизительно 12 минут.
Альфа-распад атомных ядер.
Альфа-распад - распад атомных ядер, сопровождающийся испусканием альфа-частиц (ядер 4He).
Часть изотопов могут самопроизвольно испускать альфа-частицы (испытывать альфа-распад), т.е. являются альфа-радиоактивными. Альфа-радиоактивность за редким исключением (например 8Be) не встречается среди легких и средних ядер. Подавляющее большинство альфа-радиоактивных изотопов (более 200) расположены в периодической системе в в области тяжелых ядер (Z > 83). Известно также около 20 альфа-радиоактивных изотопов среди редкоземельных элементов, кроме того, альфа-радиоактивность характерна для ядер, находящихся вблизи границы протонной стабильности. Это обусловлено тем, что альфа-распад связан с кулоновским отталкиванием, которое возрастает по мере увеличения размеров ядер быстрее (как Z2 ), чем ядерные силы притяжения, которые растут линейно с ростом массового числа A.
Ядро альфа-радиоактивно, если выполнено условие, являющееся следствием закона сохранения энергии
| M(A,Z) >M(A-4,Z-2) + Mα, | (1) |
где M(A,Z) и M(A-4,Z-2) - массы покоя исходного и конечного ядер соответственно, Mα - масса альфа-частицы. При этом в результате распада конечное ядро и альфа-частица приобретают суммарную кинетическую энергию
| Qα = ( M(A,Z) - M(A-4,Z-2) - Mα ) с2, | (2) |
которая называется энергией альфа-распада. Ядра могут испытывать альфа-распад также на возбужденные состояния конечных ядер и из возбужденных состояний начальных ядер. Поэтому соотношение для энергии альфа-распада (2) можно обобщить следующим образом
| Qα = ( M(A,Z) - M(A-4,Z-2) - Mα ) с2 + | (3) |
где 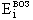 и
и 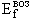 - энергии возбуждения начального и конечного ядер соответственно. Альфа-частицы, возникающие в результате распада возбужденных состояний, получили название длиннопробежных. Для большинства ядер с A > 190 и для многих ядер с 150 < A < 190 условие (12) выполняется, однако далеко не все они считаются альфа-радиоактивными. Дело в том, что современные экспериментальные возможности не позволяют обнаружить альфа-радиоактивность для нуклидов с периодом полураспада большим, чем 1016 лет. Кроме того, часть “потенциально” альфа-радиоактивных ядер испытывают также бета-распад, который сильно конкурирует с альфа-распадом.
- энергии возбуждения начального и конечного ядер соответственно. Альфа-частицы, возникающие в результате распада возбужденных состояний, получили название длиннопробежных. Для большинства ядер с A > 190 и для многих ядер с 150 < A < 190 условие (12) выполняется, однако далеко не все они считаются альфа-радиоактивными. Дело в том, что современные экспериментальные возможности не позволяют обнаружить альфа-радиоактивность для нуклидов с периодом полураспада большим, чем 1016 лет. Кроме того, часть “потенциально” альфа-радиоактивных ядер испытывают также бета-распад, который сильно конкурирует с альфа-распадом.
Основную часть энергии альфа-распада (около 98%) уносят альфа-частицы. Используя законы сохранения энергии и импульса для кинетической энергии альфа-частицы Tα можно получить соотношение
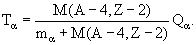
| (4) |
Периоды полураспада известных альфа-радиоактивных нуклидов варьируются от 0.298 мкс для 212Po до >1015 лет для 144Nd, 174Hf... Энергия альфа-частиц, испускаемых тяжелыми ядрами из основных состояний, составляет 4 - 9 МэВ, ядрами редкоземельных элементов 2 - 4.5 МэВ.
Важным свойством альфа-распада является то, что при небольшом изменении энергии альфа-частиц периоды полураспада меняются на многие порядки. Так у 232Th Qα = 4.08 МэВ, T1/2 = 1.41·1010 лет, а у 218Th Qα = 9.85 МэВ, T1/2 = 10 мкс. Изменению энергии в 2 раза соответствует изменение в периоде полураспада на 24 порядка.
Для четно-четных изотопов одного элемента зависимость периода полураспада от энергии альфа-распада хорошо описывается эмпирическим законом Гейгера - Неттола
| lg T1/2 = A + B/(Qα)1/2, | (5) |
где A и B - константы слабо зависящие от Z. С учетом заряда дочернего ядра Z связь между периодом полураспада T1/2 и энергией альфа-распада Qα может быть представлено в виде (B.A. Brown, Phys. Rev. c46, 811 (1992))
| lg T1/2 = 9.54Z0.6/(Qα)1/2 - 51.37, | (6) |
где T1/2 в сек, Qα в МэВ. На рис. 1 показаны экспериментальные значения периодов полураспада для 119 альфа-радиоактивных четно-четных ядер (Z от 74 до 106) и их описание с помощью соотношения (6).
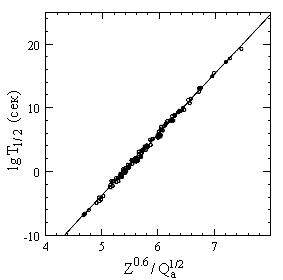 Рис. 1. Рис. 1.
|
Для нечетно-четных, четно-нечетных и нечетно-нечетных ядер общая тенденция сохраняется, но их периоды полураспада в 2 - 1000 раз больше, чем для четно-четных ядер с данными Z и Qα.
Основные особенности альфа-распада, в частности сильную зависимость вероятности альфа-распада от энергии удалось в 1928 г. объяснить Г. Гамову и независимо от него Р. Герни и Э. Кондону. Ими было показано, что вероятность альфа-распада в основном определяется вероятностью прохождения альфа-частицы сквозь потенциальный барьер.
Рассмотрим простую модель альфа-распада. Предполагается, что альфа-частица движется в сферической области радиуса R, где R - радиус ядра. Т.е. в этой модели предполагается, что альфа-частица постоянно существует в ядре.
Вероятность альфа-распада 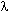 равна произведению вероятности найти альфа-частицу на границе ядра f на вероятность ee прохождения через потенциальный барьер D (прозрачность барьера)
равна произведению вероятности найти альфа-частицу на границе ядра f на вероятность ee прохождения через потенциальный барьер D (прозрачность барьера)
| λ = fD = ln2/T1/2. | (7) |
Можно отожествить f с числом соударений в единицу времени, которые испытывает альфа-частица о внутренние границы барьера, тогда
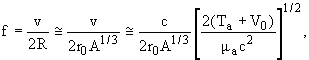
| (8) |
где v, Ta, 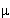 a - скорость внутри ядра, кинетическая энергия и приведенная масса альфа-частицы, V0 - ядерный потенциал. Подставив в выражение (8) V0 = 35 МэВ, Ta = 5 МэВ, получим для ядер с A
a - скорость внутри ядра, кинетическая энергия и приведенная масса альфа-частицы, V0 - ядерный потенциал. Подставив в выражение (8) V0 = 35 МэВ, Ta = 5 МэВ, получим для ядер с A 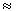 200, f
200, f 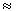 1021 с-1.
1021 с-1.
Hа рис.2 показана зависимость потенциальной энергии между альфа-частицей и остаточным ядром от расстояния между их центрами. Кулоновский потенциал обрезается на расстоянии R, которое приблизительно равно радиусу остаточного ядра. Высота кулоновского барьера Bk определяется соотношением
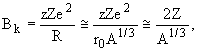 МэВ МэВ
| (9) |
Здесь Z и z - заряды (в единицах заряда электрона e) остаточного ядра и альфа-частицы соответственно. Например для 238U Bk 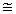 30 МэВ.
30 МэВ.
Можно выделить три области.
| 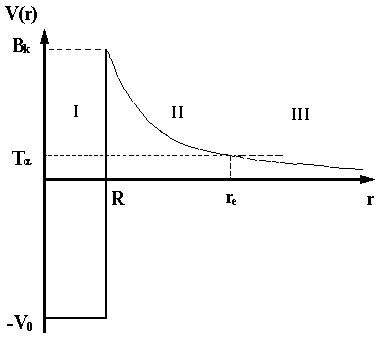 Рис. 5 Рис. 5
|
(Аналогично влияние кулоновского барьера и в случае ядерной реакции, когда альфа-частица подлетает к ядру. Если ее энергия меньше высоты кулоновского барьера, она скорее всего рассеется кулоновским полем ядра, не проникнув в него и не вызвав ядерной реакции. Вероятность таких подбарьерных реакций очень мала.)
Квантово-механическое решение задачи о прохождении частицы через потенциальный барьер дает для вероятности прохождения (коэффициента прозрачности барьера) D
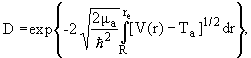
| (10) |
где μα- приведенная масса, Tα - энергия α-частицы. В приближении Tα << Bk, где Bk - высота кулоновского барьера (предполагается, что барьер чисто кулоновский) описывается соотношением
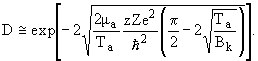
| (11) |
Рассчитанные по формулам (7), (8) и (11) периоды полураспада правильно передают важнейшую закономерность альфа-распада - сильную зависимость периода полураспада T1/2 от энергии альфа-частиц Tα(энергии альфа-распада Qα 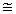 Tα ). При изменении периодов полураспада более чем на 20 порядков отличия экспериментальных значений от расчетных всего 1-2 порядка. Конечно, такие расхождения все же довольно велики. Где их источник и как надо усовершенствовать теорию, чтобы эти расхождения с экспериментом уменьшить? Какие факторы должны быть дополнительно учтены?
Tα ). При изменении периодов полураспада более чем на 20 порядков отличия экспериментальных значений от расчетных всего 1-2 порядка. Конечно, такие расхождения все же довольно велики. Где их источник и как надо усовершенствовать теорию, чтобы эти расхождения с экспериментом уменьшить? Какие факторы должны быть дополнительно учтены?
- Приведенные выше формулы описывают эмиссию альфа-частиц с нулевым орбитальным моментом l. Однако возможен распад и с ненулевым орбитальным моментом, более того, в ряде случаев распад с l = 0 запрещен законами сохранения. В этом случае к кулоновскому Vk(r) добавляется центробежный потенциал Vц(r)
| V(r) = Vk (r) + Vц (r), | (12) |
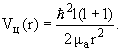
| (13) |
3. Хотя высота центробежного барьера для тяжелых ядер при l = 8 составляет всего около 10% от высоты кулоновского барьера и центробежный потенциал спадает быстрее, чем кулоновский, эффект вполне ощутим и для больших l может приводить к подавлению альфа-распада более, чем на 2 порядка.
- Результаты расчетов прозрачности барьера весьма чувствительны к средним радиусам ядер R. Так изменение R всего на 4% приводит к изменению T1/2 в 5 раз. Между тем, ядра с A > 230 могут быть сильно деформированы, что приводит к тому, что альфа-частицы охотнее вылетают вдоль большой оси эллипсоида, а средняя вероятность вылета отличается от таковой для сферического ядра. Большую чувствительность периодов полураспада от радиусов можно использовать, определяя радиусы ядер по экспериментальным значениям периодов полураспада.
- Выше никак не учитывалась структура состояний начального и конечного ядер и тесно связанная с этим проблема образования альфа-частицы в ядре, вероятность которой молчаливо полагалась равной 1. Для четно-четных ядер это приближение довольно хорошо описывает эксперимент. Однако, если перестройка структуры исходных ядер в конечные заметно затруднена, то необходимые для учета этих эффектов модификации предэкспоненциального множителя f, могут приводить к изменению расчетных значений приблизительно на два порядка.
Бета-распад атомных ядер.
Альфа-распад - распад атомных ядер, сопровождающийся испусканием альфа-частиц (ядер 4He).
Часть изотопов могут самопроизвольно испускать альфа-частицы (испытывать альфа-распад), т.е. являются альфа-радиоактивными. Альфа-радиоактивность за редким исключением (например 8Be) не встречается среди легких и средних ядер. Подавляющее большинство альфа-радиоактивных изотопов (более 200) расположены в периодической системе в в области тяжелых ядер (Z > 83). Известно также около 20 альфа-радиоактивных изотопов среди редкоземельных элементов, кроме того, альфа-радиоактивность характерна для ядер, находящихся вблизи границы протонной стабильности. Это обусловлено тем, что альфа-распад связан с кулоновским отталкиванием, которое возрастает по мере увеличения размеров ядер быстрее (как Z2 ), чем ядерные силы притяжения, которые растут линейно с ростом массового числа A.
Ядро альфа-радиоактивно, если выполнено условие, являющееся следствием закона сохранения энергии
| M(A,Z) >M(A-4,Z-2) + Mα, | (1) |
где M(A,Z) и M(A-4,Z-2) - массы покоя исходного и конечного ядер соответственно, Mα - масса альфа-частицы. При этом в результате распада конечное ядро и альфа-частица приобретают суммарную кинетическую энергию
| Qα = ( M(A,Z) - M(A-4,Z-2) - Mα ) с2, | (2) |
которая называется энергией альфа-распада. Ядра могут испытывать альфа-распад также на возбужденные состояния конечных ядер и из возбужденных состояний начальных ядер. Поэтому соотношение для энергии альфа-распада (2) можно обобщить следующим образом
| Qα = ( M(A,Z) - M(A-4,Z-2) - Mα ) с2 + | (3) |
где 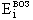 и
и 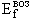 - энергии возбуждения начального и конечного ядер соответственно. Альфа-частицы, возникающие в результате распада возбужденных состояний, получили название длиннопробежных. Для большинства ядер с A > 190 и для многих ядер с 150 < A < 190 условие (12) выполняется, однако далеко не все они считаются альфа-радиоактивными. Дело в том, что современные экспериментальные возможности не позволяют обнаружить альфа-радиоактивность для нуклидов с периодом полураспада большим, чем 1016 лет. Кроме того, часть “потенциально” альфа-радиоактивных ядер испытывают также бета-распад, который сильно конкурирует с альфа-распадом.
- энергии возбуждения начального и конечного ядер соответственно. Альфа-частицы, возникающие в результате распада возбужденных состояний, получили название длиннопробежных. Для большинства ядер с A > 190 и для многих ядер с 150 < A < 190 условие (12) выполняется, однако далеко не все они считаются альфа-радиоактивными. Дело в том, что современные экспериментальные возможности не позволяют обнаружить альфа-радиоактивность для нуклидов с периодом полураспада большим, чем 1016 лет. Кроме того, часть “потенциально” альфа-радиоактивных ядер испытывают также бета-распад, который сильно конкурирует с альфа-распадом.
Основную часть энергии альфа-распада (около 98%) уносят альфа-частицы. Используя законы сохранения энергии и импульса для кинетической энергии альфа-частицы Tα можно получить соотношение
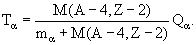
| (4) |
Периоды полураспада известных альфа-радиоактивных нуклидов варьируются от 0.298 мкс для 212Po до >1015 лет для 144Nd, 174Hf... Энергия альфа-частиц, испускаемых тяжелыми ядрами из основных состояний, составляет 4 - 9 МэВ, ядрами редкоземельных элементов 2 - 4.5 МэВ.
Важным свойством альфа-распада является то, что при небольшом изменении энергии альфа-частиц периоды полураспада меняются на многие порядки. Так у 232Th Qα = 4.08 МэВ, T1/2 = 1.41·1010 лет, а у 218Th Qα = 9.85 МэВ, T1/2 = 10 мкс. Изменению энергии в 2 раза соответствует изменение в периоде полураспада на 24 порядка.
Для четно-четных изотопов одного элемента зависимость периода полураспада от энергии альфа-распада хорошо описывается эмпирическим законом Гейгера - Неттола
| lg T1/2 = A + B/(Qα)1/2, | (5) |
где A и B - константы слабо зависящие от Z. С учетом заряда дочернего ядра Z связь между периодом полураспада T1/2 и энергией альфа-распада Qα может быть представлено в виде (B.A. Brown, Phys. Rev. c46, 811 (1992))
| lg T1/2 = 9.54Z0.6/(Qα)1/2 - 51.37, | (6) |
где T1/2 в сек, Qα в МэВ. На рис. 1 показаны экспериментальные значения периодов полураспада для 119 альфа-радиоактивных четно-четных ядер (Z от 74 до 106) и их описание с помощью соотношения (6).
 Рис. 1. Рис. 1.
|
Для нечетно-четных, четно-нечетных и нечетно-нечетных ядер общая тенденция сохраняется, но их периоды полураспада в 2 - 1000 раз больше, чем для четно-четных ядер с данными Z и Qα.
Основные особенности альфа-распада, в частности сильную зависимость вероятности альфа-распада от энергии удалось в 1928 г. объяснить Г. Гамову и независимо от него Р. Герни и Э. Кондону. Ими было показано, что вероятность альфа-распада в основном определяется вероятностью прохождения альфа-частицы сквозь потенциальный барьер.
Рассмотрим простую модель альфа-распада. Предполагается, что альфа-частица движется в сферической области радиуса R, где R - радиус ядра. Т.е. в этой модели предполагается, что альфа-частица постоянно существует в ядре.
Вероятность альфа-распада 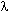 равна произведению вероятности найти альфа-частицу на границе ядра f на вероятность ee прохождения через потенциальный барьер D (прозрачность барьера)
равна произведению вероятности найти альфа-частицу на границе ядра f на вероятность ee прохождения через потенциальный барьер D (прозрачность барьера)
| λ = fD = ln2/T1/2. | (7) |
Можно отожествить f с числом соударений в единицу времени, которые испытывает альфа-частица о внутренние границы барьера, тогда
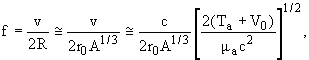
| (8) |
где v, Ta, 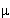 a - скорость внутри ядра, кинетическая энергия и приведенная масса альфа-частицы, V0 - ядерный потенциал. Подставив в выражение (8) V0 = 35 МэВ, Ta = 5 МэВ, получим для ядер с A
a - скорость внутри ядра, кинетическая энергия и приведенная масса альфа-частицы, V0 - ядерный потенциал. Подставив в выражение (8) V0 = 35 МэВ, Ta = 5 МэВ, получим для ядер с A 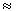 200, f
200, f 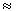 1021 с-1.
1021 с-1.
Hа рис.2 показана зависимость потенциальной энергии между альфа-частицей и остаточным ядром от расстояния между их центрами. Кулоновский потенциал обрезается на расстоянии R, которое приблизительно равно радиусу остаточного ядра. Высота кулоновского барьера Bk определяется соотношением
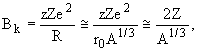 МэВ МэВ
| (9) |
Здесь Z и z - заряды (в единицах заряда электрона e) остаточного ядра и альфа-частицы соответственно. Например для 238U Bk 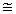 30 МэВ.
30 МэВ.
Можно выделить три области.
|  Рис. 5 Рис. 5
|
(Аналогично влияние кулоновского барьера и в случае ядерной реакции, когда альфа-частица подлетает к ядру. Если ее энергия меньше высоты кулоновского барьера, она скорее всего рассеется кулоновским полем ядра, не проникнув в него и не вызвав ядерной реакции. Вероятность таких подбарьерных реакций очень мала.)
Квантово-механическое решение задачи о прохождении частицы через потенциальный барьер дает для вероятности прохождения (коэффициента прозрачности барьера) D
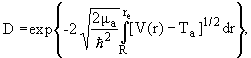
| (10) |
где μα- приведенная масса, Tα - энергия α-частицы. В приближении Tα << Bk, где Bk - высота кулоновского барьера (предполагается, что барьер чисто кулоновский) описывается соотношением
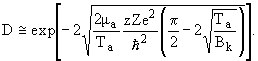
| (11) |
Рассчитанные по формулам (7), (8) и (11) периоды полураспада правильно передают важнейшую закономерность альфа-распада - сильную зависимость периода полураспада T1/2 от энергии альфа-частиц Tα (энергии альфа-распада Qα 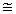 Tα ). При изменении периодов полураспада более чем на 20 порядков отличия экспериментальных значений от расчетных всего 1-2 порядка. Конечно, такие расхождения все же довольно велики. Где их источник и как надо усовершенствовать теорию, чтобы эти расхождения с экспериментом уменьшить? Какие факторы должны быть дополнительно учтены?
Tα ). При изменении периодов полураспада более чем на 20 порядков отличия экспериментальных значений от расчетных всего 1-2 порядка. Конечно, такие расхождения все же довольно велики. Где их источник и как надо усовершенствовать теорию, чтобы эти расхождения с экспериментом уменьшить? Какие факторы должны быть дополнительно учтены?
- Приведенные выше формулы описывают эмиссию альфа-частиц с нулевым орбитальным моментом l. Однако возможен распад и с ненулевым орбитальным моментом, более того, в ряде случаев распад с l = 0 запрещен законами сохранения. В этом случае к кулоновскому Vk(r) добавляется центробежный потенциал Vц(r)
| V(r) = Vk (r) + Vц (r), | (12) |
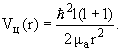
| (13) |
3. Хотя высота центробежного барьера для тяжелых ядер при l = 8 составляет всего около 10% от высоты кулоновского барьера и центробежный потенциал спадает быстрее, чем кулоновский, эффект вполне ощутим и для больших l может приводить к подавлению альфа-распада более, чем на 2 порядка.
- Результаты расчетов прозрачности барьера весьма чувствительны к средним радиусам ядер R. Так изменение R всего на 4% приводит к изменению T1/2 в 5 раз. Между тем, ядра с A > 230 могут быть сильно деформированы, что приводит к тому, что альфа-частицы охотнее вылетают вдоль большой оси эллипсоида, а средняя вероятность вылета отличается от таковой для сферического ядра. Большую чувствительность периодов полураспада от радиусов можно использовать, определяя радиусы ядер по экспериментальным значениям периодов полураспада.
- Выше никак не учитывалась структура состояний начального и конечного ядер и тесно связанная с этим проблема образования альфа-частицы в ядре, вероятность которой молчаливо полагалась равной 1. Для четно-четных ядер это приближение довольно хорошо описывает эксперимент. Однако, если перестройка структуры исходных ядер в конечные заметно затруднена, то необходимые для учета этих эффектов модификации предэкспоненциального множителя f, могут приводить к изменению расчетных значений приблизительно на два порядка.
Ядерные реакции.
Ядерная реакция – это процесс взаимодействия атомного ядра с другим ядром или элементарной частицей, сопровождающийся изменением состава и структуры ядра и выделением вторичных частиц или γ-квантов.
В результате ядерных реакций могут образовываться новые радиоактивные изотопы, которых нет на Земле в естественных условиях.
Первая ядерная реакция была осуществлена Э. Резерфордом в 1919 году в опытах по обнаружению протонов в продуктах распада ядер. Резерфорд бомбардировал атомы азота α-частицами. При соударении частиц происходила ядерная реакция, протекавшая по следующей схеме:
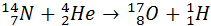
При ядерных реакциях выполняется несколько законов сохранения: импульса, энергии, момента импульса, заряда. В дополнение к этим классическим законам при ядерных реакциях выполняется закон сохранения так называемого барионного заряда (т. е. числа нуклонов – протонов и нейтронов). Выполняется также ряд других законов сохранения, специфических для ядерной физики и физики элементарных частиц.
Ядерные реакции могут протекать при бомбардировке атомов быстрыми заряженными частицами (протоны, нейтроны, α-частицы, ионы). Первая реакция такого рода была осуществлена с помощью протонов большой энергии, полученных на ускорителе, в 1932 году:
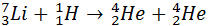
Однако наиболее интересными для практического использования являются реакции, протекающие при взаимодействии ядер с нейтронами. Так как нейтроны лишены заряда, они беспрепятственно могут проникать в атомные ядра и вызывать их превращения. Выдающийся итальянский физик Энрико Ферми первым начал изучать реакции, вызываемые нейтронами. Он обнаружил, что ядерные превращения вызываются не только быстрыми, но и медленными нейтронами, движущимися с тепловыми скоростями.
Ядерные реакции сопровождаются энергетическими превращениями. Энергетическим выходомядерной реакции называется величина
| Q = (MA + MB – MC – MD)c2 = ΔMc2. |
где MA и MB – массы исходных продуктов, MC и MD – массы конечных продуктов реакции. Величина ΔM называется дефектом масс. Ядерные реакции могут протекать с выделением (Q > 0) или с поглощением энергии (Q < 0). Во втором случае первоначальная кинетическая энергия исходных продуктов должна превышать величину |Q|, которая называется порогом реакции.
Для того чтобы ядерная реакция имела положительный энергетический выход, удельная энергия связи нуклонов в ядрах исходных продуктов должна быть меньше удельной энергии связи нуклонов в ядрах конечных продуктов. Это означает, что величина ΔM должна быть положительной.
Возможны два принципиально различных способа освобождения ядерной энергии.
1. Деление тяжелых ядер. В отличие от радиоактивного распада ядер, сопровождающегося испусканием α- или β-частиц, реакции деления – это процесс, при котором нестабильное ядро делится на два крупных фрагмента сравнимых масс.
В 1939 году немецкими учеными Отто Ганом и Фрицем Штрассманом было открыто деление ядер урана. Продолжая исследования, начатые Ферми, они установили, что при бомбардировке урана нейтронами возникают элементы средней части периодической системы – радиоактивные изотопы бария (Z = 56), криптона (Z = 36) и др.
Уран встречается в природе в виде двух изотопов: 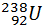 (99,3 %) и
(99,3 %) и 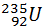 (0,7 %). При бомбардировке нейтронами ядра обоих изотопов могут расщепляться на два осколка. При этом реакция деления
(0,7 %). При бомбардировке нейтронами ядра обоих изотопов могут расщепляться на два осколка. При этом реакция деления 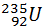 наиболее интенсивно идет на медленных (тепловых) нейтронах, в то время как ядра
наиболее интенсивно идет на медленных (тепловых) нейтронах, в то время как ядра 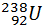 вступают в реакцию деления только с быстрыми нейтронами с энергией порядка 1 МэВ.
вступают в реакцию деления только с быстрыми нейтронами с энергией порядка 1 МэВ.
Основной интерес для ядерной энергетики представляет реакция деления ядра 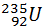 В настоящее время известны около 100 различных изотопов с массовыми числами примерно от 90 до 145, возникающих при делении этого ядра. Две типичные реакции деления этого ядра имеют вид:
В настоящее время известны около 100 различных изотопов с массовыми числами примерно от 90 до 145, возникающих при делении этого ядра. Две типичные реакции деления этого ядра имеют вид:
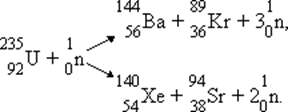
|
Обратите внимание, что в результате деления ядра, инициированного нейтроном, возникают новые нейтроны, способные вызвать реакции деления других ядер. Продуктами деления ядер урана-235 могут быть и другие изотопы бария, ксенона, стронция, рубидия и т. д.
Кинетическая энергия, выделяющаяся при делении одного ядра урана, огромна – порядка 200 МэВ. Оценку выделяющейся при делении ядра энергии можно сделать с помощью понятия удельной энергии связи нуклонов в ядре. Удельная энергия связи нуклонов в ядрах с массовым числом A ≈ 240 порядка 7,6 МэВ/нуклон, в то время как в ядрах с массовыми числами A = 90–145 удельная энергия примерно равна 8,5 МэВ/нуклон. Следовательно, при делении ядра урана освобождается энергия порядка 0,9 МэВ/нуклон или приблизительно 210 МэВ на один атом урана. При полном делении всех ядер, содержащихся в 1 г урана, выделяется такая же энергия, как и при сгорании 3 т угля или 2,5 т нефти.
Продукты деления ядра урана нестабильны, так как в них содержится значительное избыточное число нейтронов. Действительно, отношение N / Z для наиболее тяжелых ядер составляет примерно 1,6 (рис 6.6.2), для ядер с массовыми числами от 90 до 145 это отношение порядка 1,3–1,4. Поэтому ядра-осколки испытывают серию последовательных β–-распадов, в результате которых число протонов в ядре увеличивается, а число нейтронов уменьшается до тех пор, пока не образуется стабильное ядро.
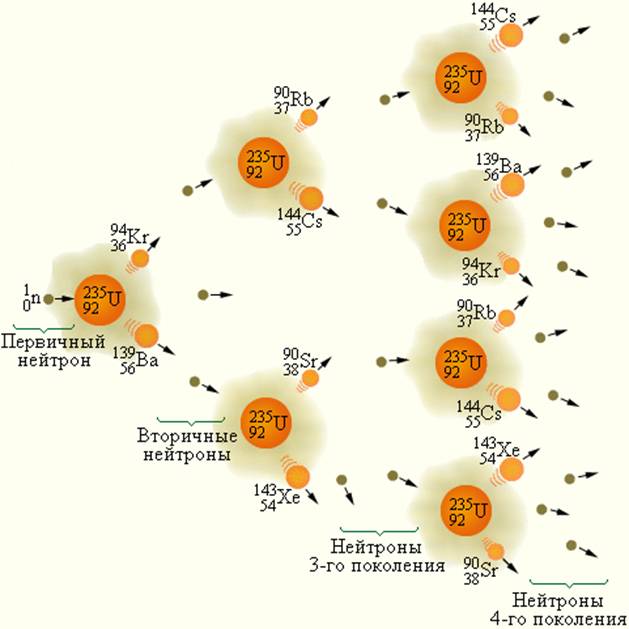
При делении ядра урана-235, которое вызвано столкновением с нейтроном, освобождается 2 или 3 нейтрона. При благоприятных условиях эти нейтроны могут попасть в другие ядра урана и вызвать их деление. На этом этапе появятся уже от 4 до 9 нейтронов, способных вызвать новые распады ядер урана и т. д. Такой лавинообразный процесс называется цепной реакцией. Схема развития цепной реакции деления ядер урана представлена на рис. 6.8.1.
|
| Рисунок 6.8.1. Схема развития цепной реакции |
Для осуществления цепной реакции необходимо, чтобы так называемый коэффициент размножения нейтронов был больше единицы. Другими словами, в каждом последующем поколении нейтронов должно быть больше, чем в предыдущем. Коэффициент размножения определяется не только числом нейтронов, образующихся в каждом элементарном акте, но и условиями, в которых протекает реакция – часть нейтронов может поглощаться другими ядрами или выходить из зоны реакции. Нейтроны, освободившиеся при делении ядер урана-235, способны вызвать деление лишь ядер этого же урана, на долю которого в природном уране приходится всего лишь 0,7 %. Такая концентрация оказывается недостаточной для начала цепной реакции. Изотоп 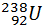 также может поглощать нейтроны, но при этом не возникает цепной реакции.
также может поглощать нейтроны, но при этом не возникает цепной реакции.
Цепная реакция в уране с повышенным содержанием урана-235 может развиваться только тогда, когда масса урана превосходит так называемую критическую массу. В небольших кусках урана большинство нейтронов, не попав ни в одно ядро, вылетают наружу. Для чистого урана-235 критическая масса составляет около 50 кг.
Критическую массу урана можно во много раз уменьшить, если использовать так называемые замедлители нейтронов. Дело в том, что нейтроны, рождающиеся при распаде ядер урана, имеют слишком большие скорости, а вероятность захвата медленных нейтронов ядрами урана-235 в сотни раз больше, чем быстрых. Наилучшим замедлителем нейтронов является тяжелая водаD2O. Обычная вода при взаимодействии с нейтронами сама превращается в тяжелую воду.
Хорошим замедлителем является также графит, ядра которого не поглощают нейтронов. При упругом взаимодействии с ядрами дейтерия или углерода нейтроны замедляются до тепловых скоростей.
Применение замедлителей нейтронов и специальной оболочки из бериллия, которая отражает нейтроны, позволяет снизить критическую массу до 250 г.
В атомных бомбах цепная неуправляемая ядерная реакция возникает при быстром соединении двух кусков урана-235, каждый из которых имеет массу несколько ниже критической.
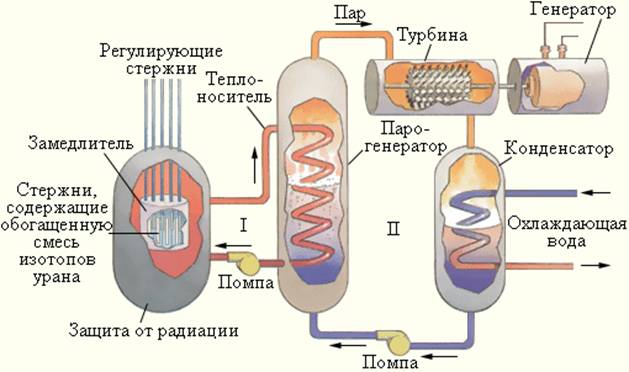
Устройство, в котором поддерживается управляемая реакция деления ядер, называется ядерным(или атомным) реактором. Схема ядерного реактора на медленных нейтронах приведена на рис. 6.8.2.
|
| Рисунок 6.8.2. Схема устройства ядерного реактора на медленных нейтронах |
Ядерная реакция протекает в активной зоне реактора, которая заполнена замедлителем и пронизана стержнями, содержащими обогащенную смесь изотопов урана с повышенным содержанием урана-235 (до 3 %). В активную зону вводятся регулирующие стержни, содержащие кадмий или бор, которые интенсивно поглощают нейтроны. Введение стержней в активную зону позволяет управлять скоростью цепной реакции.
Активная зона охлаждается с помощью прокачиваемого теплоносителя, в качестве которого может применяться вода или металл с низкой температурой плавления (например, натрий, имеющий температуру плавления 98 °C). В парогенераторе теплоноситель передает тепловую энергию воде, превращая ее в пар высокого давления, который направляется в турбину, соединенную с электрогенератором, а из турбины поступает в конденсатор. Во избежание утечки радиации контуры теплоносителя I и парогенератора II работают по замкнутым циклам.
Турбина атомной электростанции является тепловой машиной, определяющей в соответствии со вторым законом термодинамики общую эффективность станции. У современных атомных электростанций коэффициент полезного действия приблизительно равен 1/3. Следовательно, для производства 1000 МВт электрической мощности тепловая мощность реактора должна достигать 3000 МВт. 2000 МВт должны уносится водой, охлаждающей конденсатор. Это приводит к локальному перегреву естественных водоемов и последующему возникновению экологических проблем.
Однако, главная проблема состоит в обеспечении полной радиационной безопасности людей, работающих на атомных электростанциях, и предотвращении случайных выбросов радиоактивных веществ, которые в большом количестве накапливаются в активной зоне реактора. При разработке ядерных реакторов этой проблеме уделяется большое внимание. Тем не менее, после аварий на некоторых АЭС, в частности на АЭС в Пенсильвании (США, 1979 г.) и на Чернобыльской АЭС (1986 г.), проблема безопасности ядерной энергетики встала с особенной остротой.
Наряду с ядерным реактором, работающим на медленных нейтронах, большой практический интерес представляют реакторы, работающие без замедлителя на быстрых нейтронах. В таких реакторах ядерным горючим является обогащенная смесь, содержащая не менее 15 % изотопа 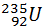 . Преимущество реакторов на быстрых нейтронах состоит в том, что при их работе ядра урана-238, поглощая нейтроны, посредством двух последовательных β–-распадов превращаются в ядра плутония, которые затем можно использовать в качестве ядерного топлива:
. Преимущество реакторов на быстрых нейтронах состоит в том, что при их работе ядра урана-238, поглощая нейтроны, посредством двух последовательных β–-распадов превращаются в ядра плутония, которые затем можно использовать в качестве ядерного топлива:
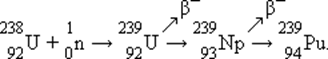
|
Коэффициент воспроизводства таких реакторов достигает 1,5, т. е. на 1 кг урана-235 получается до 1,5 кг плутония. В обычных реакторах также образуется плутоний, но в гораздо меньших количествах.
Первый ядерный реактор был построен в 1942 году в США под руководством Э. Ферми. В нашей стране первый реактор был построен в 1946 году под руководством И.В. Курчатова.
2. Термоядерные реакции. Второй путь освобождения ядерной энергии связан с реакциями синтеза. При слиянии легких ядер и образовании нового ядра должно выделяться большое количество энергии. Это видно из кривой зависимости удельной энергии связи от массового числа A (рис 6.6.1). Вплоть до ядер с массовым числом около 60 удельная энергия связи нуклонов растет с увеличением A. Поэтому синтез любого ядра с A < 60 из более легких ядер должен сопровождаться выделением энергии. Общая масса продуктов реакции синтеза будет в этом случае меньше массы первоначальных частиц.
Реакции слияния легких ядер носят название термоядерных реакций, так как они могут протекать только при очень высоких температурах. Чтобы два ядра вступили в реакцию синтеза, они должны сблизится на расстояние действия ядерных сил порядка 2·10–15 м, преодолев электрическое отталкивание их положительных зарядов. Для этого средняя кинетическая энергия теплового движения молекул должна превосходить потенциальную энергию кулоновского взаимодействия. Расчет необходимой для этого температуры T приводит к величине порядка 108–109 К. Это чрезвычайно высокая температура. При такой температуре вещество находится в полностью ионизированном состоянии, которое называется плазмой.
Энергия, которая выделяется при термоядерных реакциях, в расчете на один нуклон в несколько раз превышает удельную энергию, выделяющуюся в цепных реакциях деления ядер. Так, например, в реакции слияния ядер дейтерия и трития
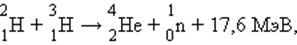
|
выделяется 3,5 МэВ/нуклон. В целом в этой реакции выделяется 17,6 МэВ. Это одна из наиболее перспективных термоядерных реакций.
Осуществление управляемых термоядерных реакций даст человечеству новый экологически чистый и практически неисчерпаемый источник энергии. Однако получение сверхвысоких температур и удержание плазмы, нагретой до миллиарда градусов, представляет собой труднейшую научно-техническую задачу на пути осуществления управляемого термоядерного синтеза.
На данном этапе развития науки и техники удалось осуществить только неуправляемую реакцию синтеза в водородной бомбе. Высокая температура, необходимая для ядерного синтеза, достигается здесь с помощью взрыва обычной урановой или плутониевой бомбы.
Термоядерные реакции играют чрезвычайно важную роль в эволюции Вселенной. Энергия излучения Солнца и звезд имеет термоядерное происхождение.
Управляемая цепная реакция
Осуществляемся в ядерном реакторе.
Я  дерный реактор
дерный реактор
Устройство, в котором осуществляется управляемая цепная реакция деления, называется ядерным реактором.
По назначению они делятся на следующие типы:
1. Исследовательские.
2. Энергетические.
3. Воспроизводящие (реакторы на быстрых нейтронах).
4. Транспортные.
5. Реакторы для промышленного получения изотопов различных химических элементов.
Р 
 еакторы, работающие на тепловых нейтронах, состоят из делящегося вещества (изотоп урана, торий или плутоний), замедлителя нейтронов (графит, тяжелая вода, обычная вода), отражателя нейтронов (вещество, которое служит замедлителем), системы управления ходом цепной реакции деления (управляющие стержни из соединений бора и кадмия, эффективно поглощающие нейтроны), системы охлаждения, предназначенной для отвода тепла из активной зоны реактора (вода, жидкие металлы, некоторые органические жидкости), системы дозиметрического контроля и биологической защиты окружающей среды от протонов, нейтронов иγ-излучений.
еакторы, работающие на тепловых нейтронах, состоят из делящегося вещества (изотоп урана, торий или плутоний), замедлителя нейтронов (графит, тяжелая вода, обычная вода), отражателя нейтронов (вещество, которое служит замедлителем), системы управления ходом цепной реакции деления (управляющие стержни из соединений бора и кадмия, эффективно поглощающие нейтроны), системы охлаждения, предназначенной для отвода тепла из активной зоны реактора (вода, жидкие металлы, некоторые органические жидкости), системы дозиметрического контроля и биологической защиты окружающей среды от протонов, нейтронов иγ-излучений.
Условием возникновения цепной реакции в реакторе является наличие размножения нейтронов при делении ядер и при k = 1.
Управление реактором осуществляется стержнями, которые поглощают нейтроны. Если эти стержни полностью ввести в активную зону, то k<l; если их постепенно выводить из активной зоны, то k> 1.
Энергия деления ядер выделяется в виде тепла, которое используется для получения пара, вращающего турбину
Реакторы на быстрых нейтронах имеют преимущество: при их работе образуется значительное количество плутония, который затем можно использовать как ядерное топливо. Реакцию можно поддерживать лишь в обогащенной смеси, содержащей не менее 15% изотопа 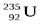 .
.
В реакторах размножителях коэффициент воспроизводства k может быть равен 1,5, т.е. при делении 1 кг урана получается 1,5 кг плутония. В обычных реакторах k = 0,6–0,7.
Таким образом, при делении ядер 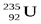 реактор одновременно воспроизводит ядерное горючее
реактор одновременно воспроизводит ядерное горючее 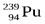 в количестве, превосходя тем израсходованное.
в количестве, превосходя тем израсходованное.
Выделение нескольких нейтронов при делении ядер создает возможность для осуществления ценной реакции. Вероятность захвата медленных нейтронов с последующим делением в сотни раз больше, чем быстрых.
Контролируя среду, в которой делятся ядра, можно создать условия, где на каждую реакцию деления в среднем приходится один вылетающий нейтрон, вызывающий последующую реакцию деления.
Термоядерная реакция
Реакция слияния легких ядер при очень высокой температуре, сопровождающаяся выделением энергии, называется термоядерной реакцией.
Для слияния необходимо, чтобы расстояние между ядрами приблизительно было равно 10−12 см.
Однако этому препятствуют кулоновские силы. Они могут быть преодолены при большой кинетической энергии. Особенно большое практическое значение имеет тот факт, что при этой реакции на каждый нуклон выделяется значительно намного больше энергии, чем при ядерной реакции, например, при синтезе ядра гелия из ядер водорода выделяется энергия, равная 6 МэВ, а при делении ядра урана 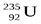 на один нуклон приходится ≈0,9 МэВ.
на один нуклон приходится ≈0,9 МэВ.
Пример термоядерной реакции: 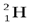 +
+ 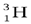 →
→ 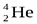 +
+ 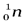 .
.
В этом случае выделяется энергия, равная 17,6 МэВ.
Управляемая термоядерная реакция – энергетически выгодная реакция. Может идти при больших температурах (порядка несколько сотен млн. градусов). При большой плотности вещества такая температура может быть достигнута путем создания в плазме мощных электронных разрядов. Проблема: трудно удержать плазму.
Самоподдерживающиеся термоядерные реакции происходят в недрах Земли. В настоящее время в России и ряде других стран ведутся работы по осуществлению управляемой термоядерной реакции.
Явление электромагнитной индукции. Правило Ленца. Закон Фарадея. Объяснение закона Фарадея на основе закона сохранения энергии.
Электромагнитная индукция – явление возникновения тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего его.
Явление электромагнитной индукции было открыто М. Фарадеем.
Опыты Фарадея
· На одну непроводящую основу были намотаны две катушки: витки первой катушки были расположены между витками второй. Витки одной катушки были замкнуты на гальванометр, а второй – подключены к источнику тока. При замыкании ключа и протекании тока по второй катушке в первой возникал импульс тока. При размыкании ключа также наблюдался импульс тока, но ток через гальванометр тек в противоположном направлении.
· Первая катушка была подключена к источнику тока, вторая, подключенная к гальванометру, перемещалась относительно нее. При приближении или удалении катушки фиксировался ток.
· Катушка замкнута на гальванометр, а магнит движется – вдвигается (выдвигается) – относительно катушки.
· Опыты показали, что индукционный ток возникает только при изменении линий магнитной индукции. Направление тока будет различно при увеличении числа линий и при их уменьшении.
· Сила индукционного тока зависит от скорости изменения магнитного потока. Может изменяться само поле, или контур может перемещаться в неоднородном магнитном поле.
Направление индукционного тока определяется по правилу Ленца: индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток.
Закон Фарадея можно сформулировать еще таким образом: э.д.с. ξi электромагнитной индукции в контуре численно равна и противоположна по знаку скорости изменения магнитного потока сквозь поверхность, ограниченную этим контуром. Этот закон является универсальным: э.д.с. ξi не зависит от способа изменения магнитного потока.
Э.д.с. электромагнитной индукции выражается в вольтах. Действительно, учитывая, что единицей магнитного потока является вебер (Вб), получим
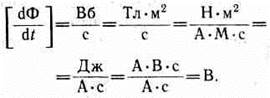
Обобщая результаты своих многочисленных опытов, Фарадей пришел к количественному закону электромагнитной индукции. Он показал, что всякий раз, когда происходит изменение сцепленного с контуром потока магнитной индукции, в контуре возникает индукционный ток; возникновение индукционного тока указывает на наличие в цепи электродвижущей силы, называемой электродвижущей силой электромагнитной индукции. Значение индукционного тока, а следовательно, и э. д. с, электромагнитной индукции ξi определяются только скоростью изменения магнитного потока, т. е.

Теперь необходимо выяснить знак ξi. В § 120 было показано, что знак магнитного потока зависит от выбора положительной нормали к контуру. В свою очередь, положительное направление нормали связано с током правилом правого винта (см. § 109). Следовательно, выбирая определенное положительное направление нормали, мы определяем как знак потока магнитной индукции, так и направление тока и э.д.с. в контуре. Пользуясь этими представлениями и выводами, можно соответственно прийти к формулировке закона электромагнитной индукции Фарадея: какова бы ни была причина изменения потока магнитной индукции, охватываемого замкнутым проводящим контуром, возникающая в контуре э.д.с.
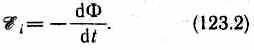
Знак минус показывает, что увеличение потока (dФ/dt>0) вызывает э.д.с. ξξi<0, т. е. поле индукционного тока направлено навстречу потоку; уменьшение потока (dФ/dt<0 ) вызывает ξi>0,
Дата: 2019-02-19, просмотров: 411.