MS Excel имеет набор специальных функций для работы с матрицами. Это МОБР() – вычисление обратной матрицы. МОПРЕД() – вычисление определителя матрицы. МУМНОЖ() – возвращает матричное произведение двух матриц.
Пример. Решить систему линейных уравнений 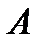 x = b матричным методом.
x = b матричным методом.
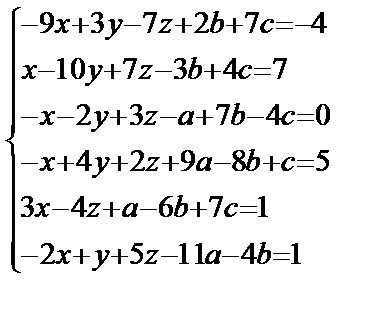
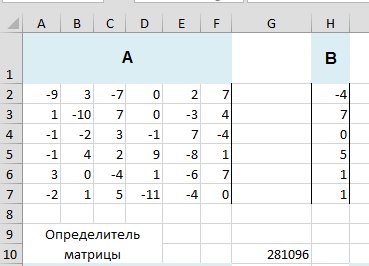
Для решения системы линейных уравнений вида АХ=В (вычисления вектора-столбца Х) необходимо найти для матрицы А обратную матрицу А-1 и умножить ее на вектор-столбец В свободных членов. В диапазон А2:F7 вводим матрицу А, в диапазон H2:H7 вводим матрицу В. Найдем определитель матрицы А с помощью функции Microsoft Excel «=МОПРЕД(A2:F7)» в ячейке G10. Он не равен 0 (= -241422), значит обратная матрица существует.
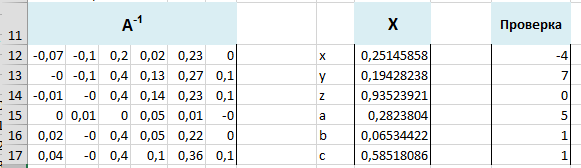
Для вычисления обратной матрицы выделим диапазон А12:F17 и вставим функцию =МОБР(A2:F7), завершаем ввод нажатием комбинацией клавиш <Ctrl>+<Shift>+<Enter>. Для вычисления вектора-столбца Х выделяем диапазон I12:I17, вставляем формулу =МУМНОЖ(A12:F17;H2:H7), завершая ее ввод нажатием комбинацией клавиш <Ctrl>+<Shift>+<Enter>. Данная формула перемножает обратную матрицу А с матрицей В. В диапазоне I12:I17 получится матрица решения Х. Для проверки вводим в диапазон K12:K17 формулу =МУМНОЖ(A2:F7;I12:I17), перемножающую матрицу А с матрицей решения Х, в результате получаем, идентичную матрице свободных членов.
Построение графика.
Пример. Построим график f(x)=Sin(2x) на промежутке от [-5,5] с шагом 1.
Сначала заполним столбец Х значениями от -5 до 5 с шагом 1, используя маркер автозаполнения. Затем введем формулу для определения функции и скопируем ее на весь диапазон. Выделяем диапазон для х и f(x) и используем команду Вставка диаграмму – Точечная:
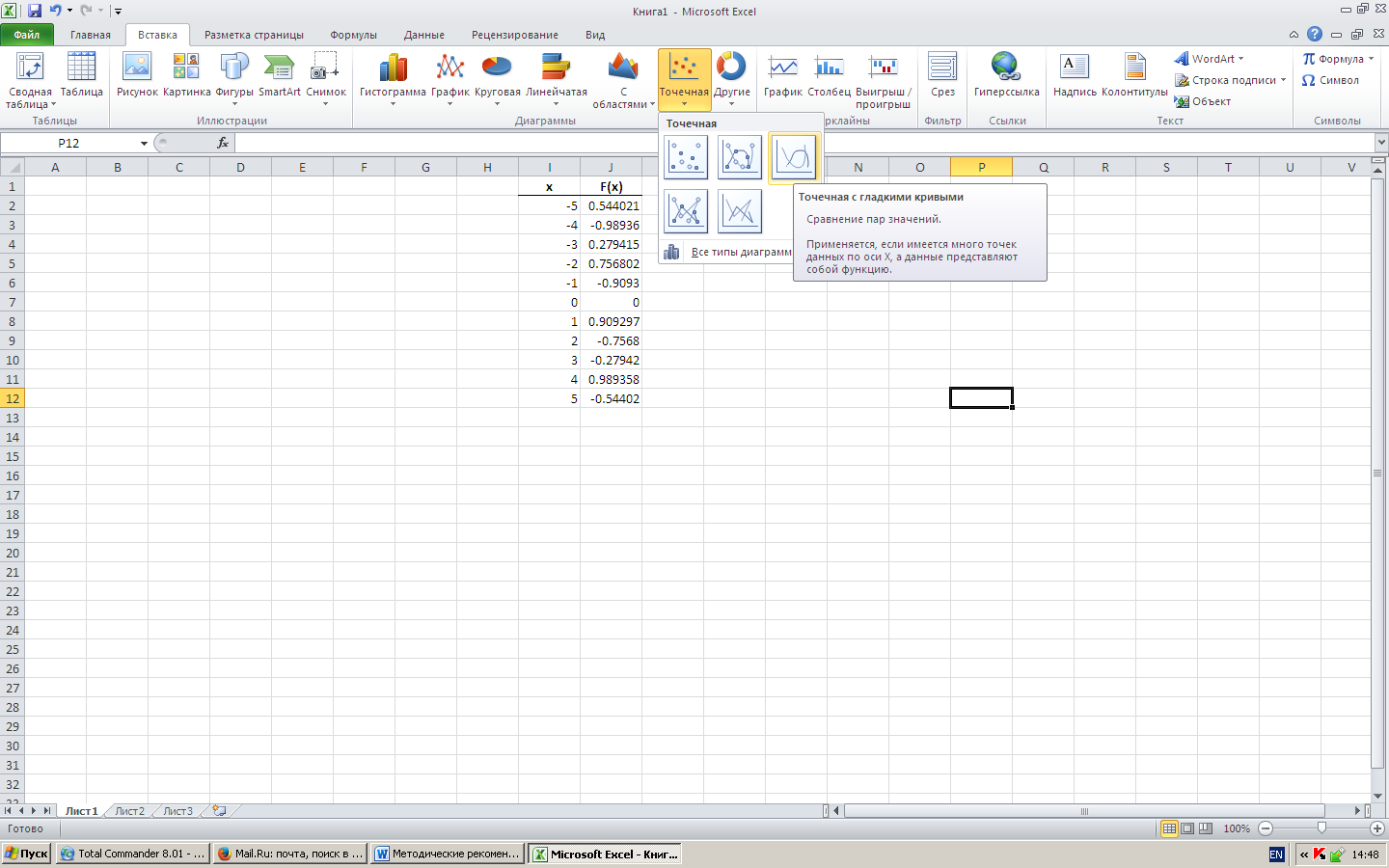
Полученный график:
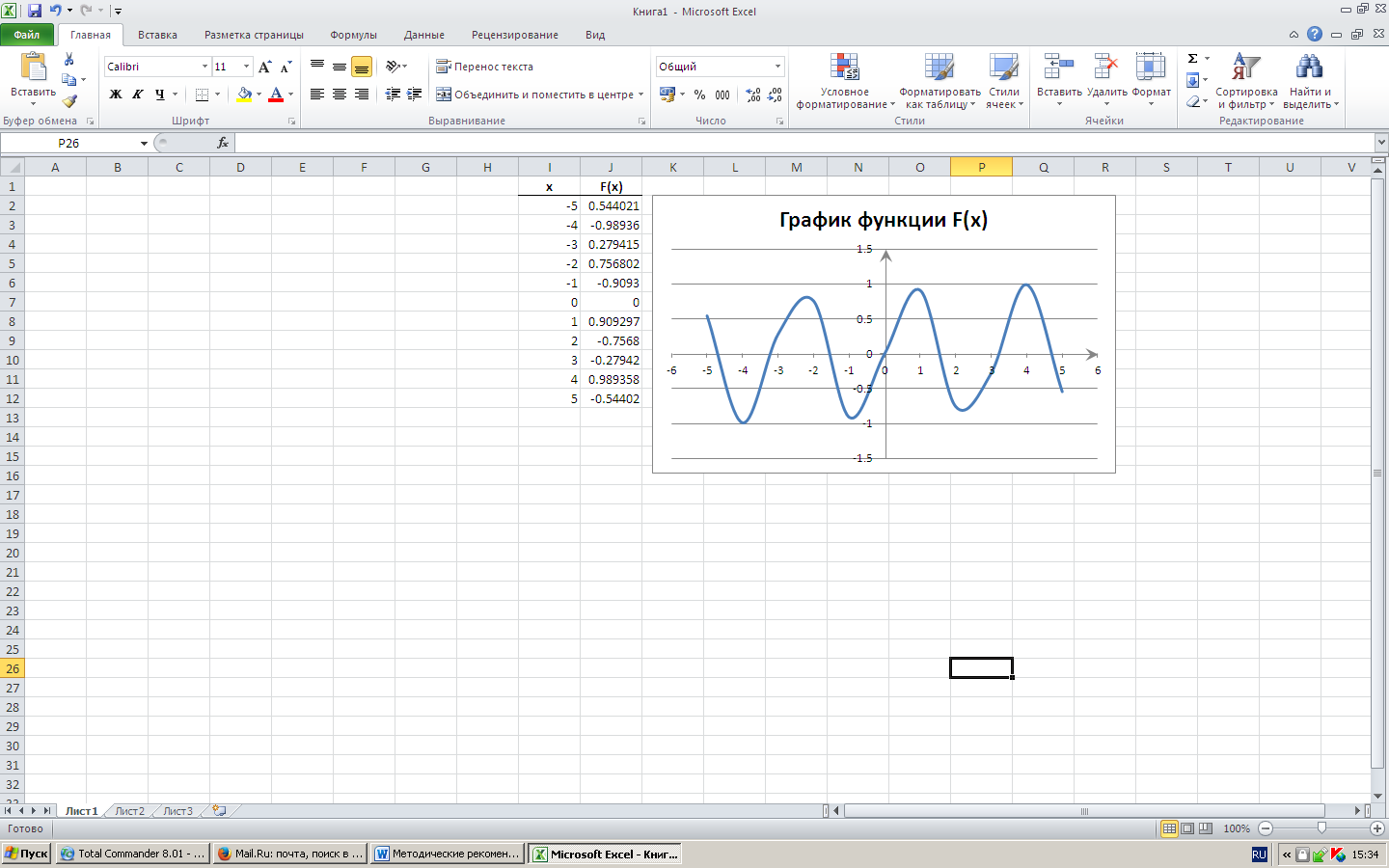
Построение графика функции, заданной в полярных координатах.
Часто различные линии на плоскости задаются в полярных координатах, общее уравнение которых можно записать в виде
F ( ρ , φ )=0,
где ρ,φ – полярные координаты.
Если линия задана уравнением ρ=ρ(φ) в полярных координатах, то уравнение ее уравнение в декартовых координатах можно записать в виде:
х=ρ(φ)· Cos ( φ )
y =ρ(φ)· Sin ( φ )
Для этого следует:
1. Подготовить диапазон изменения координаты φ.
2. Рассчитать значение функции на данной диапазоне в полярных координатах ρ=ρ(φ).
3. Рассчитать значения х, у в декартовой системе координат по формулам:
х=ρ(φ)· Cos ( φ )
y =ρ(φ)· Sin ( φ ).
4. Выделить диапазон области определения в области значения функции, т. е. все значения х, у и, используя команду Вставка диаграмму – Точечная, строим график.
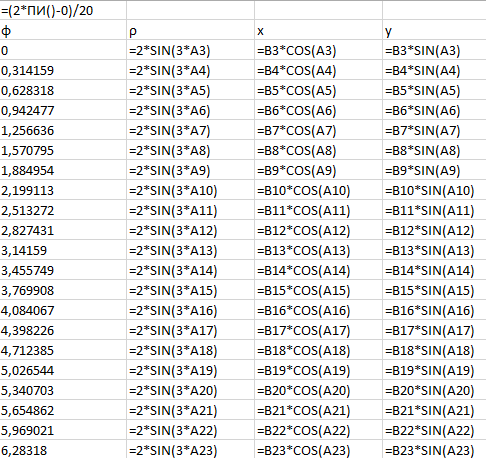
Пример. Построить функцию, заданную уравнением в полярных координатах:
ρ=2·Sin(3·φ)
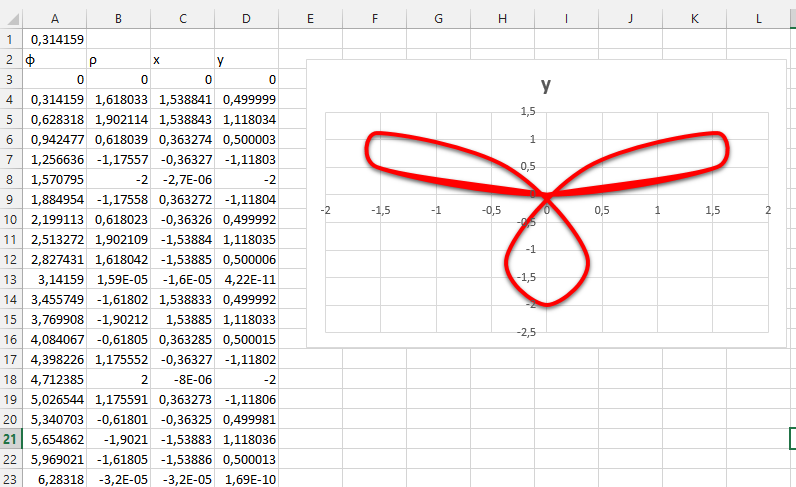
| 
|
Надстройка «Поиск решения».
В MS Excel существует возможность с помощью надстройки «Поиск решения» (вкладка «Данные») найти решение, оптимальное в некотором смысле. Для нахождения корней заданной точности нелинейного уравнения, локальных максимумов и минимумов можно использовать данную надстройку. Предварительно необходимо построить график. «Поиск решения» необходимо настроить с помощью команд из меню «Сервис».
Пример. Найти действительные корни уравнения x5+2x4+5x3+8x2-7x-3=0 с точностью 0,000001 на заданном промежутке [-4,4] .с шагом 1, воспользовавшись функцией «Поиск решения».
Сначала построим график функции, чтобы определить количество корней на данном участке. Из графика мы определяем, что на данном промежутке находятся три корня.
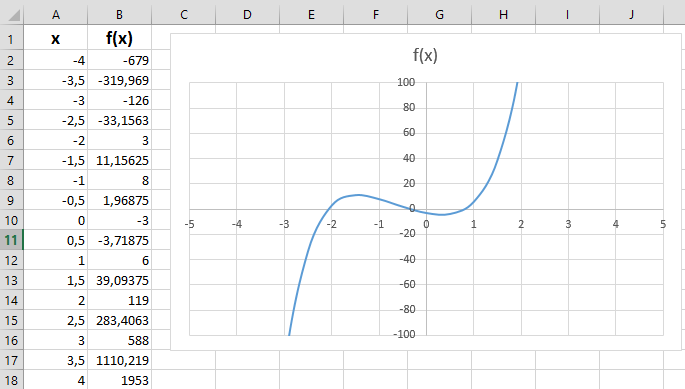
Определяем первый корень уравнения с заданной точностью, используя функцию «Поиск решения». В ячейку L2 размещаем приближенное значение корня – (0), а ячейку M2 копируем формулу из любой ячейки столбца B с вычислениями данной функции. Формула в ячейке M2 должна обязательно ссылаться на ячейку L2. Вызываем команду «Поиск решения» из меню «Данные».
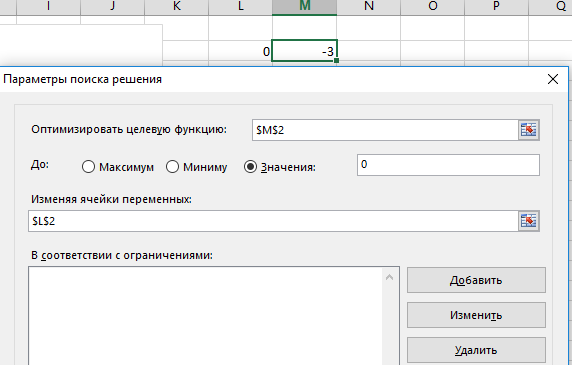
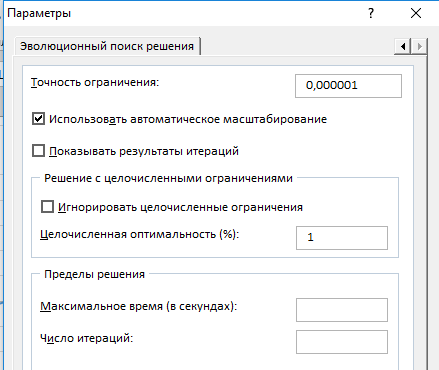
В открывающемся диалоговом окне вводим следующие значение полей. Установить целевую ячейку - «$M$2» равной значению – 0, изменяя ячейки $L$2. С помощью кнопки «Параметры» открывается следующее окно, в котором устанавливаем относительную погрешность 0,000001.
Возвращаемся в окно «Поиск решения» и нажимаем кнопку «Выполнить» и получаем значение корня с заданной точностью.
Получаем результат:
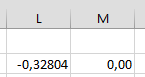
Аналогичным образом находим оставшиеся два корня, используя «Поиск решения». Для нахождения локального минимума устанавливаем целевую ячейку равной минимальному значению. Для нахождения локального максимума в открывающемся диалоговом окне устанавливаем целевую ячейку равной максимальному значению.
Метод наименьших квадратов
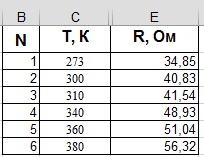
На основании исследования зависимости сопротивления проводника R от температуры получены экспериментальные данные:
| Т, К | R, Ом |
| 273 | 34,85 |
| 300 | 40,83 |
| 310 | 41,54 |
| 340 | 48,93 |
| 360 | 51,04 |
| 380 | 56,32 |
Определить коэффициенты линейной регрессии методом наименьших квадратов. Построить зависимость R от Т.
Задача заключается в нахождении коэффициентов линейной зависимости, при которых функция двух переменных а и b 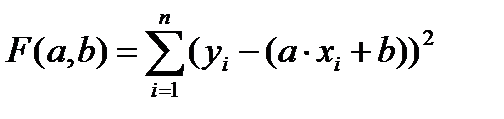 принимает наименьшее значение. То есть, при данных а и b сумма квадратов отклонений экспериментальных данных от найденной прямой будет наименьшей. В этом вся суть метода наименьших квадратов.
принимает наименьшее значение. То есть, при данных а и b сумма квадратов отклонений экспериментальных данных от найденной прямой будет наименьшей. В этом вся суть метода наименьших квадратов.
Таким образом, решение примера сводится к нахождению экстремума функции двух переменных.
Составляется и решается система из двух уравнений с двумя неизвестными. Находим частные производные функции 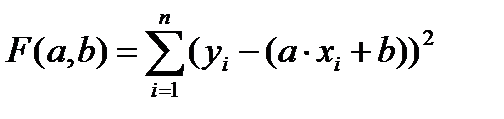 по переменным а и b, приравниваем эти производные к нулю.
по переменным а и b, приравниваем эти производные к нулю.
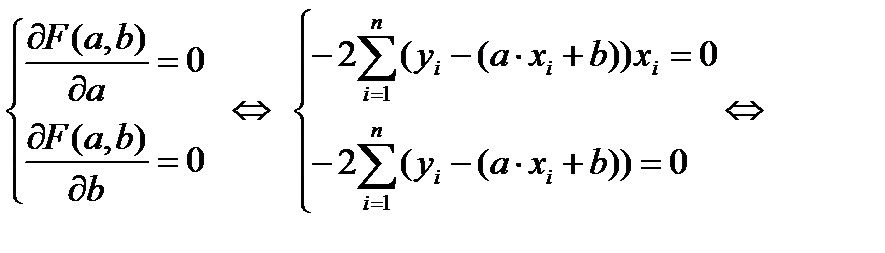
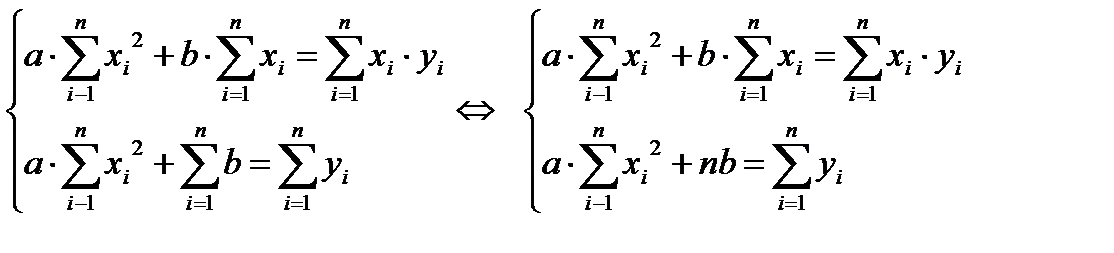
Решаем полученную систему уравнений любым методом (методом подстановки или методом Крамера) и получаем формулы для нахождения коэффициентов по методу наименьших квадратов (МНК).
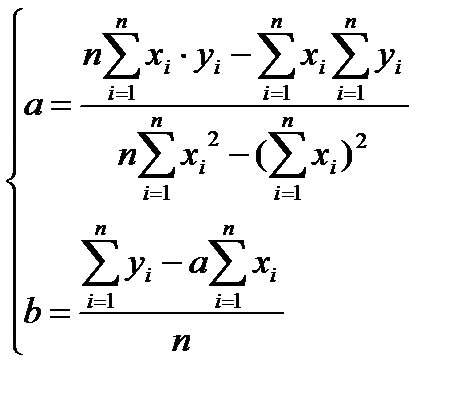
При данных а и b функция 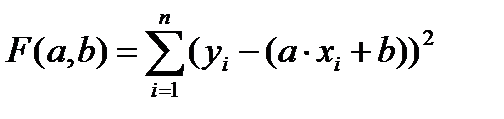 принимает наименьшее значение. Формула для нахождения параметра a содержит суммы
принимает наименьшее значение. Формула для нахождения параметра a содержит суммы 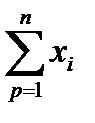 ,
, 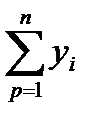 ,
, 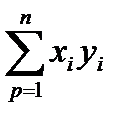 ,
, 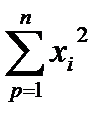 и параметр n - количество экспериментальных данных. Коэффициент b находится после вычисления a.
и параметр n - количество экспериментальных данных. Коэффициент b находится после вычисления a.
Введем начальные данные
Вычислим значения сумм 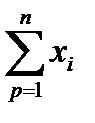 ,
, 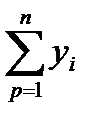 ,
, 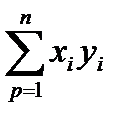 ,
, 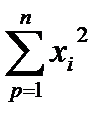 , х – Т, у - R.
, х – Т, у - R.
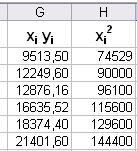
| 
|
Согласно формулам вычислим коэффициенты а и b линейной регрессии:

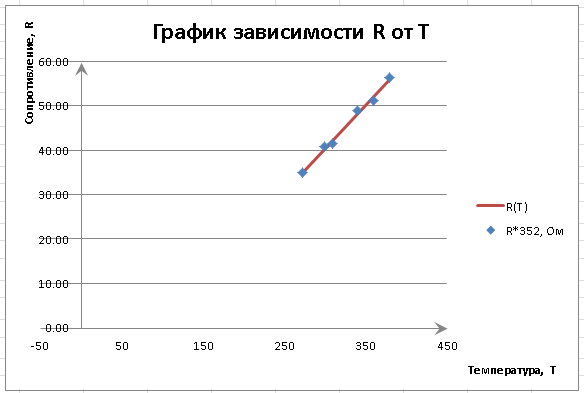
Прямая R(T) = 0,196154∙T – 18,5909 - искомая аппроксимирующая прямая.
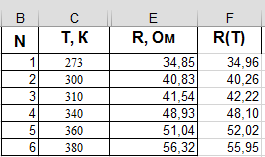
График зависимости R от Т. Красная линия – это искомая аппроксимирующая прямая, синие точки – это исходные данные.
Microsoft Access
Дата: 2019-02-25, просмотров: 411.