Вычисления в таблицах программы Excel осуществляется при помощи формул. Формула может содержать числовые константы, ссылки на ячейки и функции Excel, соединенная знаками математических операций. Если ячейка содержит формулу, то в рабочем листе отображается текущий результат вычисления этой формулы. Если сделать ячейку текущей, то сама формула отображается в строке формул. Чтобы добавить формулу к рабочей таблице, ее нужно ввести в ячейку. Можно удалять, перемещать, копировать формулы, точно так же, как и другие данные. При изменении начальных данных программа выполняет перерасчет данных.
Операторы, которые используются в формулах: +(сложение), -(вычитание), *(умножение), /(деление), ^(возведение в степень), =(логическое равно), <(больше чем), >(меньше чем), >=(больше или равно), <=(меньше или равно), <>(не равно).
Ввод формул
Предположим надо в ячейку А3 ввести формулу, которая позволит сложить данные, находящиеся в ячейках А1 и А2. Для этого необходимо активизировать ячейку А3 (т.е. ту ячейку, в которую мы вводим формул), набрать с клавиатуры знак = (с этого знака начинается ввод формул), затем щелкнуть мышкой по ячейке А1 (можно вводить адрес ячейки помощью клавиатуры, в формуле появится адрес данной ячейки), набрать знак сложения, затем щелкнуть по ячейке А2(в формуле появится адрес этой ячейки) и завершить ввод (используя клавишу “Enter” или щелкнуть по значку Ú на синем поле перед строкой формул.
Относительные, абсолютные, смешанные ссылки
| А | В | С | |
| 1 | 3 | 10 | =А1+В1 |
| 2 | 5 | 11 | =А2+В2 |
| 3 | 7 | 12 | =А3+В3 |
Если скопировать формулу в другие ячейки, то Excel вставит туда не копию этой формулы, она ее видоизменит. Программа изменяет ссылки на ячейки, которые есть в первоначальной формуле в соответствии с новым положением формулы. Предположим, что первоначальная инструкция содержит инструкцию о сложении значения, расположенного на две ячейки левее и значения, расположенного на одну ячейку левее. При копировании формулы данная инструкция тоже копируется, в результате чего в новой формуле видоизменяются адреса ячеек. Такие ссылки на ячейки называют относительными.
Бывают случаи, когда необходимо, чтобы адреса ячеек копировались точь в точь. В таких случаях ссылки называют абсолютными.
| А | В | С | |
| 1 | Курс доллара | Цена в долларах | Цена в бел. Руб. |
| 2 | 2000 | 4 | =$А$2*В2 |
| 3 | 8 | =$А$2*В3 | |
| 4 | 10 | =$А$2*В4 |
В данном случае адрес ячейки, в котором указан курс доллара, должен не меняться при копировании формулы. В абсолютной ссылке используются в адресе ячейки два знака доллара, один перед столбцом, другой перед строкой. И это говорит о том, что ссылка на данную ячейку является неизменной.
В Excel существуют также смешанные ссылки, в которых одна часть адреса, относящаяся к столбцу или строке, является абсолютной, а другая – относительной.
| А | В | С | |
| 1 | Значения | 5 % | 7 % |
| 2 | 100 | =$A2*B$1 | =$A2*C$1 |
| 3 | 200 | =$A3*B$1 | =$A3*C$1 |
| 4 | 300 | =$A4*B$1 | =$A4*C$1 |
В ссылке $A2 при копировании остается постоянным столбец, а строка меняется, а в ссылке B$1 остается постоянной строка, а столбец меняется. Знак $ можно ввести в ручную, а можно использовать функциональную клавишу F4. Первое нажатие переводит А2 в $А$2, второе - А$2, третье - $А2, четвертое - А2.
Пример. Для вычисления определенного интеграла 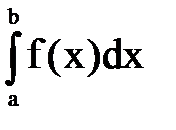 на отрезке [a, b] можно использовать формулу трапеций
на отрезке [a, b] можно использовать формулу трапеций
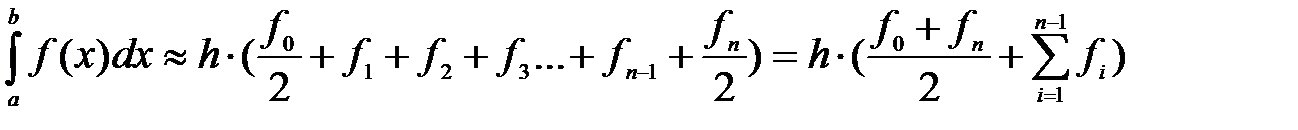 , где
, где 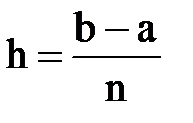 ,
,
Границы элементарных отрезков xi =a + i*h, а значения функции в этих точках fi = f(xi), где i = 0, 1, …, n.
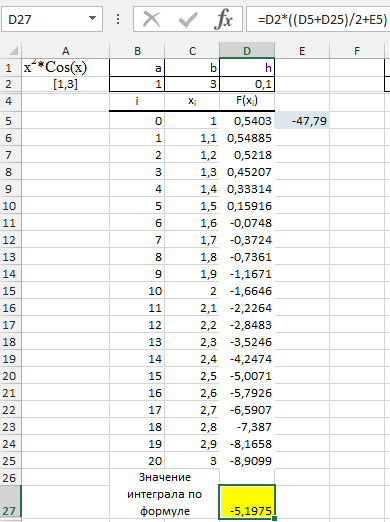
Рассчитаем значение определенного интеграла для f(x)= x2*Cos(x) при n=20 на [0, 3]. (Указание. Необходимо составить таблицы для значений i, xi, рассчитать значения 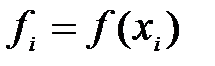 , а затем используя формулу трапеций, найти определенный интеграл.
, а затем используя формулу трапеций, найти определенный интеграл.
Введем исходные данные: в ячейку В2 – начальное значение х0 - а=1, в ячейку С2 – конечное значение хn - в=3, для вычисления h (т.е.шага) в ячейку D2 введем формулу =($C$2-$B$2)/20.
В ячейки В5:В25 введем значения i. В ячейку C5 вводим начальное значение 1, в ячейку С6 – вводим значение, равное (1 + h) = 1,1, выделяем эти две ячейки и с помощью маркера заполнения заполняем диапазон С7:С25 значениями с шагом 0,1.
В ячейках D5:D25 рассчитываем значения функции для хi, для этого в ячейку D5 вводим формулу =C5^2*(COS(C5))и копируем эту формулу во весь диапазон. В ячейке Е5 вводим формулу =СУММ(D6:D24), т.е. вычисляем сумму значений функции для всех хi, кроме начального и конечного значения х. В ячейку D27 вводим формулу трапеций =D2*((D5+D25)/2+E5). Получаем результат – (-5,19746).
Работа с функциями.
Функции - это встроенные инструменты, которые используются в формулах. Функции позволяют:
· Упрощать формулы;
· Выполнять по формулам такие вычисления, которые невозможно сделать по-другому;
· Ускорять выполнения некоторых задач редактирования;
· Выполнять условное вычисление по формулам, благодаря чему можно реализовывать алгоритмы принятых решений.
Приведем пример, как встроенная функция позволяет упростить формулу необходимо найти среднее значение – формула =(А1+А2+А3+А4+А5)/5; используя встроенную функцию эта формула будет иметь вид =СРЗНАЧ(А1:А5). Предположим, надо узнать максимальное значение из диапазона А1:А100. Это можно сделать, используя функцию =МАКС(А1:А100). Предположим, что нужно подсчитать в рабочей таблице комиссионные по результатам продаж какого-либо товара. Если продавец продал продукции большее, чем на 1000 000, то ставка составляет 7,5%, если меньше, то 5%. Без использования функции пришлось бы создать две разные формулы и правильно употреблять их для каждого значения объема продаж. С помощью функции получим =ЕСЛИ(А1<1000000;А1*0,05;А1*0,075). Во всех функциях используются круглые скобки. Данные внутри круглых скобок называются аргументами. Функции различаются по тому, как они используют аргументы. В зависимости от этого различают следующие типы функций:
1. Функции без аргументов;
2. Функции с одним аргументом;
3. Функции с фиксированным числом аргументов;
4. Функции с неопределенным числом аргументов;
5. Функции с необязательными аргументами.
Даже, если функция не использует аргумент, то все равно с названием функции будут пустые скобки =СЛЧИС() (возвращает случайное число 0 или 1). Если в функция используется несколько аргументов, то каждый из них отделяется точкой с запятой. Если диапазону задано имя, то запись функции будет иметь вид =СУММ(А1:А20) =СУММ(Продажи), где диапазон А1:А20 имеет имя Продажи. Если в качестве аргумента используется весь столбец, то получим =СУММ(В:В).
Литералом называют число или строку текста, которые непосредственно заданы в качестве аргументов функции =КОРЕНЬ(225).
В качестве аргументов можно использовать выражения. Выражения можно считать формулой внутри формулы. Когда Excel сталкивается с выражением в качестве аргумента функции, программа вначале вычисляет его, а затем использует полученный результат в качестве значения аргумента функции, например: =КОРЕНЬ((А1^2))+(А2^2)). В выражении могут встречаться другие функции. Функции, которые используются в формуле в качестве аргумента других функций, называются вложенными. Сначала программа вычисляет значение вложенной функции =SIN(РАДИАНЫ(В9)). Функция РАДИАНЫ преобразует значение аргумента, заданного в градусах, в радианы, поскольку во всех геометрических функциях Excel аргументы задаются именно в радианах. Поэтому, если в ячейке В9 значение угла измеряется в градусах, сначала функция РАДИАНЫ преобразует его в радианы, а затем функция SIN вычислит синус угла.
Способы ввода функций
Функции могут вводиться вручную (с помощью клавиатуры вводится имя функции и список ее аргументов)
С использованием средства Мастер функций (выбирается команда «Функция» из меню «Вставка» или используется соответствующая кнопка на панели инструментов). Появляется диалоговое окно Мастера функции. В правой части окна будет указано 10 последних недавно использованных функций. А в левой части окна будут указаны категории функций. Все функции разбиты на категории. При выборе одной из категории в правом окне «Функции» появится перечень функций, включенных в эту категорию. В окне есть краткое описание функции.
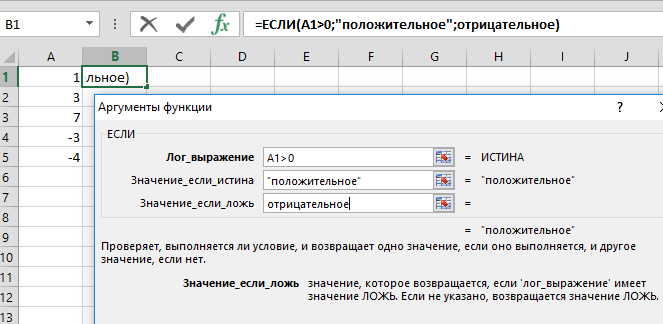
Функция ЕСЛИ.
В функции ЕСЛИ используют три аргумента. Первый – это логическое выражение, которое может принимать значение «истина» или «ложь». Второй и третий аргументы – это такие выражения, которые вычисляются в случае, если первый аргумент принимает соответственно истинное или ложное значение.
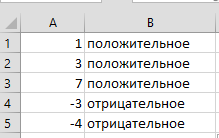
Пример – формула возвращает строку «положительный», если значение ячейки А1>0, и «отрицательный» в противном случае. =ЕСЛИ(А1>0; «положительный»; «отрицательный»).
Результат:
Если необходимо в таблице с числовыми данными указать три значения, то надо использовать вложенную функцию ЕСЛИ.
Пример. Построить в одной системе координат графики функции на промежутке [-10,10] с шагом 0,5.
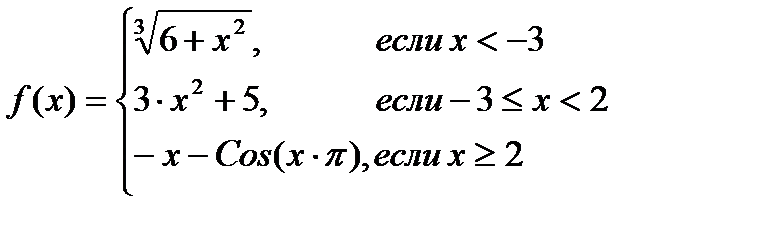
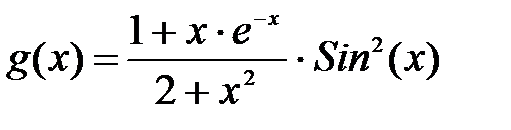
В ячейки B2:B42 вводим значения х от -10 до 10 с шагом 0,5 (заполняем ячейку B2 значением -10, B3 = -9,5, выделяем эти две ячейки и с помощью маркера заполнения заполняем значениями диапазон B4:B42) . В ячейки C2 вводим формулу для вычисления функции F(x) =ЕСЛИ(B2<-3;(6+B2^2)^(1/3);ЕСЛИ(B2>=2;-1*B2-COS(B2*ПИ()); 3*B2^2+5)) и копируем на весь диапазон C3:C42. Используем вложенную функцию ЕСЛИ для определения значения функции для трех различных диапазонах значения х.
В ячейку D2 вводим формулу =(1+B2*EXP(-1*B2))/(2+B2^2)*(SIN(B2))^2 для функции G(x) и копируем с помощью маркера автозаполнения на весь диапазон D3:D42.
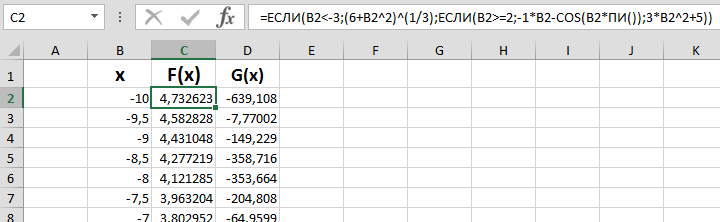
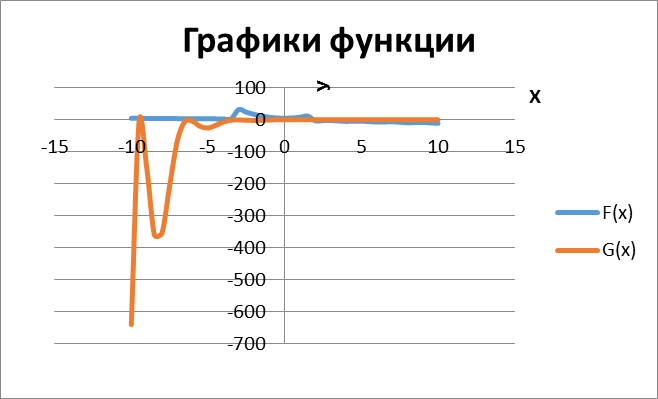
Выделяем диапазон В2:D42 и строим график, используя команды Вставка – Диаграммы – Точечная. Получаем результат:
Дата: 2019-02-25, просмотров: 353.