Для событий рассчитывают три основные характеристики: ранний и поздний срок совершения события, а также его резерв.
Ранний срок свершения события tр определяется величиной наиболее длительного отрезка пути от исходного до рассматриваемого события, причем tр(1) = 0, a tp(N) = tкр (Lкр)
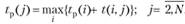 (3.46)
(3.46)
Поздний срок свершения события tп характеризует самый поздний допустимый срок, к которому должно совершаться событие, не вызывая при этом срыва срока свершения конечного события:
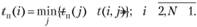 (3.47)
(3.47)
Этот показатель определяется "обратным ходом", начиная с завершающего события, с учетом соотношения tn(N) = tр(N).
Все события, за исключением событий, принадлежащих критическому пути, имеют резерв R(i):
 (3.48)
(3.48)
Резерв показывает, на какой предельно допустимый срок можно задержать наступление этого события, не вызывая при этом увеличения срока выполнения всего комплекса работ.
Для всех работ (i,j) на основе ранних и поздних сроков свершения событий можно определить следующие показатели (здесь и в дальнейшем, где это целесообразно, для упрощения записей все подстрочные символы заменяются строчными):
Ранний срок начала - 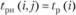 , (3.49)
, (3.49)
Ранний срок окончания -  , (3.50)
, (3.50)
Поздний срок окончания - 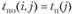 , (3.51)
, (3.51)
Поздний срок начала - 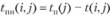 , (3.52)
, (3.52)
Полный резерв времени - 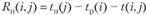 , (3.53)
, (3.53)
Независимый резерв времени -
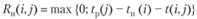 (3.54)
(3.54)
или
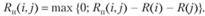 (3.55)
(3.55)
Полный резерв времени показывает, на сколько можно увеличить время выполнения конкретной работы при условии, что срок выполнения всего комплекса работ не изменится.
Независимый резерв времени соответствует случаю, когда все предшествующие работы заканчиваются в поздние сроки, а все последующие - начинаются в ранние сроки. Использование этого резерва не влияет на величину резервов времени друг их работ.
Путь характеризуется двумя показателями - продолжительностью и резервом. Продолжительность пути определяется суммой продолжительностей составляющих его работ. Резерв определяется как разность между длинами критического и рассматриваемого путей. Из этого определения следует, что работы, лежащие на критическом пути, и сам критический путь имеют нулевой резерв времени. Резерв времени пути показывает, на сколько может увеличиться продолжительность работ, составляющих данный путь, без изменения продолжительности общего срока выполнения всех работ.
Названные выше характеристики СМ могут быть получены на основе аналитических формул (3.46)-(3.55), а процесс вычислений отображается либо на самом графике СМ, либо в матрице размерности N x N, либо в таблице. Рассмотрим алгоритмы табличного метода расчета сетевого графика на конкретном примере решения задачи организации труда при реализации некоторого проекта.
Пример 3.11. Пусть реализуется проект по строительству АЗС, при этом привлекаемые рабочие могут выполнять любую из выделенных по принятой технологии работ. Менеджер проекта установил, что в данном проекте от начала до завершения работ можно выделить 5 событий, и существуют 6 различных видов работ, связывающих эти события. При первоначальном распределении рабочих по видам работ по имеющимся нормативам трудоемкости были рассчитаны длительности выполнения работ (в днях), таким образом, сетевой график реализации данного проекта имеет вид модели, представленной ранее на рис. 3.7.
Требуется рассчитать основные характеристики событий, работ и всей сетевой модели в целом, а также определить наличие резерва для некоторых работ в целях оптимизации модели и сокращения сроков выполнения проекта за счет перераспределения рабочих по видам работ.
Рассмотрим этапы табличного метода расчета данной сетевой модели; результаты этого расчета приведены в табл. 3.17 в графах 1-9.
Этап 1. Перечень работ и их продолжительность запишем во вторую и третью графы табл. 3.17, при этом работы записываются последовательно в гр. 2: сперва начинающиеся с номера 1, затем с номера 2 и т.д.
Этап 2. В первой графе поставим число Кпр, показывающее количество работ, непосредственно предшествующих событию i, с которого начинается рассматриваемая работа. Для работ, начинающихся с номера 1, предшествующих работ нет (Кпр = 0). Для работы, начинающейся на номер k, просматриваются все верхние строчки второй графы и отыскиваются работы, заканчивающиеся на этот номер k. Количество найденных работ записывается в первую графу во все строчки, соответствующие работам, начинающимся с номера k. Например, для работы (4, 5) в графу 1 поставим цифру 2, так как на номер 4 оканчиваются две работы: (1,4) и (3,4).
Таблица 3.17
| Kпр | (i, j) | t(i, j) | tpн(i, j) = tp(i, j) | tpo(i, j) | tпн(i, j) | tпо(i, j) = tп(i, j) | Rп | Rн | Кн |
| 1 | 2 | 3 | 4 | 5 = 4 + 3 | 6 = 7 - 3 | 7 | 8 | 9 | 10 |
| 0 | (1,2) | 6 | 0 | 6 | 0 | 6 | 0 | 0 | 0,71 |
| 0 | (1,3) | 0 | 0 | Э | 0 | 0 | 0 | 0 | 1 |
| 0 | (1,4) | 8 | 0 | 8 | 9 | 17 | 9 | 9 | 0,47 |
| 1 | (2,5) | 9 | 6 | 15 | 12 | 21 | 6 | 0 | 0,71 |
| 1 | (3,4) | 12 | 0 | 17 | 0 | 17 | 0 | 0 | 1 |
| 2 | (4,5) | 4 | 17 | 21 | 17 | 21 | 0 | 0 | 1 |
Этап 3. Заполнение таблицы начинается с расчета раннего срока работ tp(i). Для работ, имеющих цифру "ноль" в первой графе, в графе 4 также заносятся нули и рассчитываются соответствующие значения для графы 5 (ранний срок окончания как суммы соответствующих чисел в графе 4 и графе 3 (см. формулу (3.51)). В нашей модели таких работ три; в первой строчке графы 5 ставим 0 + 6 = 6, аналогично по второй и третьей строке.
Для заполнения следующих строк графы 4 для работ (i,j) просматриваются заполненные строки графы 5, содержащие работы, оканчивающиеся на номер i, и максимальное из найденных значений (если их несколько) переносится в графу 4 для обрабатываемых строк. Так, в нашем примере в четвертой строке в графе 4 ставим 6, а в графе 5 - 15 (6 + 9 = 15). Аналогично в пятой строке в графе 4 и графе 5 ставим соответственно 5 и 17 (5 + 12 = 17). В последней шестой строке в графе 4 ставим 17 (наибольшее из чисел 8 и 17 в графе 5) и соответственно в графу 5 ставим 21 (17 + 4 = 21).
Этап 4. Графы 7 и 6 заполняются "обратным ходом", т.е. снизу вверх. Для этого просматриваются строки (работы), оканчивающиеся на номер N последнего события, и из графы 5 выбирается максимальная величина; эта величина записывается в графу 7 по всем строчкам, оканчивающимся на N (см. формулу (3.51)), с учетом равенства tп (N) = tp(N). Затем заполняется графа 6 по этим строкам как разность между графой 7 и графой 3 (см. формулу (3.52)). В нашем примере таких строк две (четвертая и шестая), для которых в графе 5 стоят числа 15 и 21; выбираем наибольшее из них (21) и записываем его в графу 7 по этим строкам, после чего заносим соответствующие числа в графу 6.
Далее просматриваются строки, оканчивающиеся на номер события, предшествующего завершающему, т.е. на (N - 1). Для этих строк просматриваются все строчки графы 6, лежащие ниже и начинающиеся с номера (N - 1); среди них в графе 6 выбирается минимальная величина, которая переносится в графу 7 по обрабатываемым строкам, после чего заполняется графа 6. В нашем примере таких строк две (третья и пятая); ниже их с номера 4 начинается одна (последняя) работа, и в графе 6 стоит 17, следовательно, в графе 7 по этим строчкам ставим число 17, после чего заполняется графа 6.
Затем аналогичный процесс повторяется для строк, оканчивающихся на (N - 2), (N - 3) и т.д. до тех пор, пока не будут заполнены все строки по графы 7 и 6. В нашем примере результаты приведены в соответствующих графах табл. 3.17.
Этап 5. Показатели графы 8 рассчитываются как разности соответствующих показателей граф 6 и 4 или граф 7 и 5 (см. формулы (3.48) или (3.53)). Чтобы заполнить графу 9, можно предварительно рассчитать резервы времени каждого события по формуле (3.48), а затем воспользоваться формулой (3.55). В нашем примере резервы времени для каждого из пяти событий равны соответственно: R(1) = 0; R(2) = 12 - 6 = 6; R(3) = 5 - 5 = 0; R(4) = 17 - 17 = 0; R(5) = 0. Последующие результаты по формуле (3.55) приведены в графе 9 табл. 3.17.
Этап 6. На этом этапе подводятся основные итоги расчета. Учитывая, что нулевой резерв времени имеют только работы (Rп = 0) и события (R(i) = 0), которые принадлежат критическому пути, получаем, что критическим является путь LKp = (1, 3, 4, 5), продолжительность которого (tкр) равна 21 дню. Так как работы (1, 2), (1, 4) и (2, 5) имеют ненулевые резервы Rп, то очевидно, что путем перевода некоторого числа рабочих с этих работ на работы, принадлежащие критическому пути, можно сократить продолжительность этого пути и тем самым сократить сроки выполнения проекта в целом, т.е. осуществить оптимизацию сетевого графика.
Оптимизация сетевых моделей
Для оптимизации сетевой модели, выражающейся в перераспределении ресурсов с ненапряженных работ на критические для ускорения их выполнения, необходимо как можно более точно оценить степень трудности своевременного выполнения всех работ, а также "цепочек" пути. Более точным инструментом решения этой задачи по сравнению с полным резервом является коэффициент напряженности, который может быть вычислен одним их двух способов в соответствии с приведенной ниже формулой:
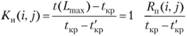 (3.56)
(3.56)
где t(Lmax) - продолжительность максимального пути, проходящего через работу (i, j);
t'кp - общая продолжительность отрезков пути, проходящего через работу (i, j), совпадающих с критическим путем.
Коэффициент напряженности изменяется от нуля до единицы, причем чем он ближе к единице, тем сложнее выполнить данную работу в установленный срок. Самыми напряженными являются работы критического пути, для которых коэффициент напряженности равен 1. На основе значений этого коэффициента все работы СМ могут быть разделены на три группы:
- напряженные (Kн(i,j) > 0,8);
- подкритические (0,6 < Kn(i,j) < 0,8);
- резервные (Kн(i,j) < 0,6).
В результате перераспределения ресурсов стараются максимально уменьшить общую продолжительность работ, что возможно при переводе всех работ в первую группу.
Пример 3.12. Рассчитаем коэффициенты напряженности всех работ сетевой модели, рассматриваемой выше в примере 3.11. При расчете этих показателей по формуле (3.56) целесообразно пользоваться графиком данной СМ, представленным на рис. 3.7. Для работ критического пути (1, 3), (3, 4) и (4, 5) коэффициенты напряженности Кн = 1. Для других работ:
Кн(1, 2) = 1 - (6: (21 - 0)) = 0,71;
Кн(1, 4) = 1 - (9: (21 -4)) = 0,47;
Кн(2, 5) = 1 - (6 : (21 - 0)) = 0,71.
Результаты расчетов приведены в графе 10 (Кн) табл. 3.17. Они показывают, что напряженными являются работы критического пути (1, 3), (3, 4) и (4, 5); работы (1, 2) и (2, 5) являются подкритическими, а работа (1, 4) - резервная. Следовательно, оптимизация рассматриваемой СМ возможна в основном за счет резервной работы (1, 4) и частично за счет подкритических работ (1,2) и (2, 5).
Если данный расчет СМ проведен до начала работ, менеджер проекта может скорректировать первоначальное распределение рабочих по видам работ, сняв некоторое количество рабочих с работы (1, 4) и, возможно, с работ (1, 2) и (2, 5) и распределив их по работам критического пути (1, 3), (3, 4) и (4, 5).
В результате работы, не лежащие на критическом пути, несколько увеличат свою продолжительность, а продолжительность работ критического пути сократится; тем самым при той же численности рабочих сократится срок реализации проекта в целом. Получив новый вариант сетевого графика, менеджер может повторить аналогичные расчеты, добиваясь путем перераспределения рабочих наиболее оптимального варианта СМ и, следовательно, наилучшего распределения рабочих по видам работ.
Сетевое планирование в условиях неопределенности
В рассмотренных выше примерах сроки выполнения отдельных видов работ определялись при условии взаимозаменяемости рабочих и при наличии нормативов трудоемкости для данных работ. на практике во многих случаях трудно точно определить продолжительность работ, поэтому задаются две оценки этой продолжительности - минимальная и максимальная. Минимальная оценка tmin(i,j) дает продолжительность работ при наиболее благоприятных обстоятельствах, а максимальная tmax(i,j) - при наиболее неблагоприятных. Продолжительность работы в этом случае рассматривается как случайная величина, которая при реализации может принять любое значение в заданном интервале. Такие оценки являются вероятностными, и их ожидаемые значения tож(i,j) оцениваются по-разному в зависимости от принятого закона распределения. Так, при бета-распределении плотности вероятности ожидаемое значение продолжительности работ (математическое ожидание) задается формулой
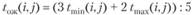 (3.57)
(3.57)
Для характеристики степени разброса возможных значений относительно ожидаемого уровня используется показатель дисперсии:
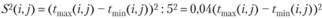 (3.58)
(3.58)
На основе этих оценок можно рассчитать все характеристики СМ, однако они будут выступать как средние характеристики. При достаточно большом количестве работ можно утверждать, что общая продолжительность любого пути, включая критический, имеет нормальный закон распределения со средним значением, равным сумме средних значений продолжительности составляющих его работ, и дисперсией, равной сумме дисперсий этих же работ.
Кроме основных характеристик СМ, при вероятностном задании продолжительности работ можно решить две важные задачи:
1. определить вероятность того, что продолжительность критического пути tкp не превысит заданного (директивного) уровня Т;
2. определить максимальный срок выполнения всего комплекса работ Т при заданном уровне вероятности (надежности) р.
Более подробно вопросы сетевого планирования в условиях неопределенности с решением конкретных примеров рассмотрены в ряде учебных и научных изданий (см. например, параграф 3.6 в [15]).
Дата: 2019-02-25, просмотров: 340.