Задача нелинейного программирования формулируется так же, как и общая задача оптимального программирования, т.е. в виде (3.37)-(3.39), со следующими требованиями к целевой функции и допустимой области: целевая функция 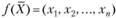или (и) хотя бы одна из функций 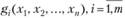являются нелинейными:

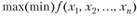(3.37)

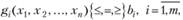(3.38)

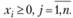(3.39)

Напомним, что для задач линейного программирования характерно следующее.

o Множество допустимых решений выпукло. Это выпуклое множество имеет конечное число вершин, называемых обычно крайними (угловыми) точками.

o Множество всех точек 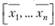n-мерного пространства, в которых целевая функция принимает заданное значение, есть гиперплоскость (линия) уровня. Кроме того, гиперплоскости, соответствующие разным значениям целевой функции, параллельны.

o Локальный max или min является также глобальным max или min целевой функции на множестве допустимых решений, т.е. не существует локального оптимума целевой функции, отличного от глобального оптимума.

o Если оптимальное значение целевой функции ограничено, то но крайней одна крайняя точка множества допустимых решений является оптимальным решением. Кроме того, начав с произвольной вершины множества допустимых решений, можно достичь оптимума за конечное число шагов, причем на каждом шаге совершается переход только в соседнюю вершину. Окончательно данная вершина является оптимальной тогда и только тогда, когда значение целевой функции в ней, по крайней мере, не меньше, чем значения целевой функции во всех примыкающих вершинах.

У произвольной задачи нелинейного программирования некоторые или все приведенные выше свойства ЗЛП отсутствуют. Вследствие этого задачи нелинейного программирования несравненно сложнее задач ЛП и для них не существует общего универсального метода решения (аналогичного симплексному методу).

Пример 3.8. Найти шах и min функции 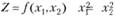при ограничениях

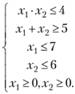
Решение. Линии уровня целевой функции (Z = const) представляют собой окружности с центром в начале координат; область допустимых решений не является выпуклой и состоит из двух отдельных частей (на рис. 3.6 эти части заштрихованы, линии уровня показаны пунктиром). Минимальное значение функции Z = 17 достигается в точках А(1; 4) и L(4; 1). Функция Z имеет два локальных максимума: в точке £>(2/3; 6), где функция 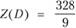, и в точке M(7; 4/7), в которой функция Z(M) = 2417/49.

Точка М - точка глобального максимума (рис. 3.6).

Особое место занимают задачи типа

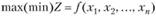(3.40)

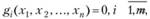(3.41)

для решения которых можно воспользоваться классическим методом оптимизации Лагранжа, или методом разрешающих множителей. При этом предполагают, что функции f и g_i (i = 1,m) непрерывны вместе со своими первыми частными производными. Для решения задачи составляют функцию Лагранжа

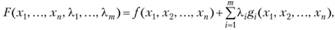
определяют частные производные этой функции по переменным 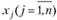и множителям Лагранжа 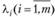, приравнивают их нулю и получают систему уравнений:

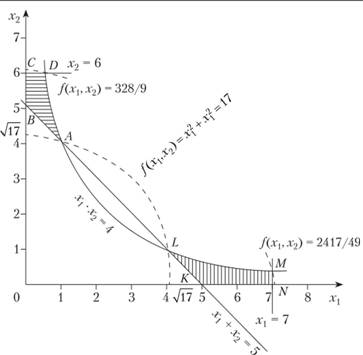
Рис. 3.6

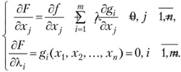(3.42)

В основе метода Лагранжа решения классической задачи оптимизации (3.40), (3.41) лежит утверждение, что если функция 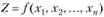в точке 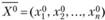имеет экстремум, то существует такой вектор 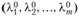, что точка 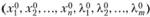является решением системы (3.42). Следовательно, решая систему (3.42), получаем множество стационарных точек, в которых функция Z может иметь экстремальные значения. При этом, как правило, неизвестен способ определения точек глобального максимума или минимума. Однако если решения системы найдены, то для определения глобального максимума или минимума достаточно найти значения функции в соответствующих точках области определения.

Пример 3.9. Найти экстремум функции 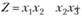при ограничениях

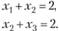
Решение. Составляем функцию Лагранжа

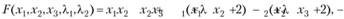
дифференцируем ее по переменным .г₎,х₂,ХзД₎Д2 и полученные выражения приравниваем нулю:

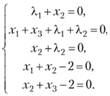
Из первого и третьего уравнений следует, что 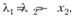поэтому

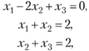
откуда 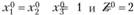. Поскольку, например, точка (0; 2; 0) принадлежит допустимой области и в ней Z = 0, то делаем вывод, что точка (1; 1; 1) - точка глобального максимума.

К классу задач нелинейного программирования, изученному наиболее основательно, относятся задачи с линейными ограничениями и нелинейной целевой функцией. В общем виде такая задача записывается следующим образом:

найти ,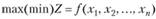

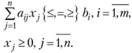
Отметим, что даже для задач с линейными ограничениями вычислительные методы разработаны лишь в тех случаях, когда целевая функция имеет определенные свойства, например, функция Z - сепарабельная, т.е.

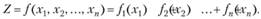
Чтобы гарантировать возможность отыскания оптимального решения, на функции /;(*,) должны быть наложены добавочные ограничения. Другим примером могут служить задачи, в которых целевая функция может быть записана как сумма линейной и квадратичной форм, так что

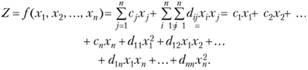
Такие нелинейные задачи называются задачами квадратичного программирования. Чтобы быть уверенным, что оптимальное решение и в этом случае может быть найдено, на величины d_Vj следует наложить некоторые ограничения.

Имеются достаточно эффективные методы решения задачи выпуклого программирования, т.е. задачи минимизации нелинейной, но гладкой выпуклой функции при ограничениях, заданных нелинейными неравенствами, определяющими выпуклое множество переменных:

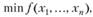(3.43)

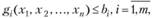(3.44)

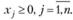(3.45)

В случае максимизации в таких задачах целевая функция должна быть вогнутой. Симплексный алгоритм для решения общей задачи ЛП представляет собой итеративную процедуру, с помощью которой точное оптимальное решение может быть получено за конечное число шагов. Для задач нелинейного программирования вычислительный метод, дающий точное оптимальное решение за конечное число шагов, удается построить не всегда. Здесь часто приходится соглашаться на использование методов, дающих только приближенное решение или требующих для сходимости бесконечного числа шагов.

Один из наиболее мощных методов решения задач нелинейного программирования состоит в преобразовании задачи каким-либо образом к виду, допускающему применение симплексного алгоритма. Природа "преобразования", с помощью которого нелинейная задача может быть приведена к форме, допускающей применение симплексного метода, очень сильно зависит от типа задачи. В некоторых случаях не требуется никакой предварительной аппроксимации, в других аппроксимация нужна. Однако эта аппроксимация может быть сделана сколь угодно точной (ценой увеличения объема вычислений).

Широко применяется градиентный метод. Он представляет собой итеративную процедуру, в которой переходят шаг за шагом от одного допустимого решения к другому так, что значение целевой функции улучшается. Однако в отличие от симплексного метода ЛП в нем не используется переход от одной вершины к другой. Вообще говоря, для сходимости к решению здесь требуется бесконечное число итераций.

Широкое применение нашли методы штрафных функций и барьеров. Метод штрафных функций аппроксимирует задачу с ограничениями задачей без ограничений с функцией, которая налагает штраф за выход из допустимой области.

Идея метода барьеров аналогична методу штрафных функций, однако аппроксимация здесь осуществляется "изнутри" допустимой области.

Весьма полезным вычислительным методом для решения некоторых типов задач нелинейного программирования является метод динамического программирования (ДП). При решении задачи этим методом процесс решения расчленяется на этапы, решаемые последовательно во времени и приводящие, в конечном счете, к искомому решению. Типичные особенности многоэтапных (многошаговых) задач, решаемых методом динамического программирования, состоят в следующем.

o Процесс перехода производственно-экономической системы из одного состояния в другое должен быть марковским (процессом с отсутствием последействия). Это значит, что если система находится в некотором состоянии 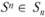, то дальнейшее развитие процесса зависит только от данного состояния и не зависит от того, каким путем система приведена в это состояние.

o Процесс длится определенное число шагов N. На каждом шаге осуществляется выбор одного управления uⁿ, под воздействием которого система переходит из одного состояния Sⁿ в другое 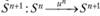. Поскольку процесс марковский, то иⁿ = uⁿ(Sⁿ) зависит только от текущего состояния.

o Каждый шаг (выбор очередного решения) связан с определенным эффектом, который зависит от текущего состояния и принятого решения: φ_n(Sⁿ, uⁿ).

o Общий эффект (доход) за N шагов слагается из доходов на отдельных шагах, т.е. критерий оптимальности должен быть аддитивным (или приводящимся к нему).

Требуется найти такое решение uⁿ для каждого шага (п = 1, 2, 3,..., N), т.е. последовательность (u¹,..., u^N), чтобы получить максимальный эффект (доход) за N шагов.

Любая возможная допустимая последовательность решений (u¹,..., u^N) называется стратегией управления. Стратегия управления, доставляющая максимум критерию оптимальности, называется оптимальной.

В основе общей концепции метода ДП лежит принцип оптимальности Беллмана.

Оптимальная стратегия обладает таким свойством, что независимо от того, каким образом система оказалась в рассматриваемом конкретном состоянии, последующие решения должны составлять оптимальную стратегию, привязывающуюся к этому состоянию. Математически этот принцип записывается в виде рекуррентного соотношения ДП (РДП):

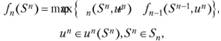
где uⁿ(Sⁿ) - все допустимые управления при условии, что система находится в состоянии Sⁿ;

φ_n(Sⁿ, uⁿ) - эффект от принятия решения uⁿ;

fⁿ(Sⁿ) - эффект за оставшиеся п шагов.

Благодаря принципу оптимальности удается при последующих переходах испытывать не все возможные варианты, а лишь оптимальные выходы. РДП позволяют заменить трудоемкое вычисление оптимума по N переменным в исходной задаче решением N задач, в каждой из которых оптимум находит лишь по одной переменной.

Имеется очень много практически важных задач, которые ставятся и решаются как задачи ДП (задачи о замене оборудования, о ранце, распределения ресурсов и т.д.)

В качестве примера построения РДП рассмотрим использование принципа оптимальности для реализации математической модели задачи оптимального распределения некоторого ресурса в объеме х:

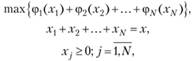
где x_j- количество ресурса, используемое j-м способом;

φ_n(x_j) - доход от применения способа .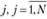

Рекуррентные соотношения, с помощью которых находится решение этой задачи, имеют вид:

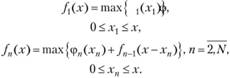
Пример 3.10. Найти максимум функции 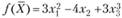при ограничениях

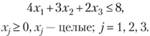
Решение. Целевая функция задачи 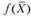является аддитивной, так как ее можно представить в виде суммы функций f_j(x_j), каждая из которых зависит только от одной переменной х_j.

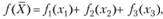
где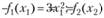

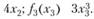
Находим 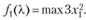Поскольку на переменные x_j накладываются условия целочисленности и неотрицательности, то знак 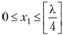(знак [] обозначает целую часть числа, т.е. наибольшее целое число, не превосходящее данное); таким образом, x₁ Î {0,1,2}. Для каждого фиксированного значения l вычисляем значение функции f₁(l) выбираем среди них максимальное, при этом в соответствии с ограничениями задачи X может принимать все целые значения от 0 до 8. Далее вычисляем:

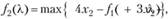
для всех ;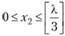

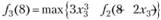
для всех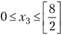

Все вычисления приведены в табл.3.16.

Таким образом, max 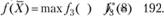Оптимальную стратегию находим следующим образом. Сначала устанавливаем, что 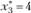(соответствует максимальному значению 192). Значение 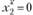находим из соответствующих граф табл. 3.16 для 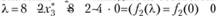при ).

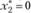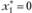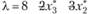
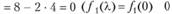Далее находим значение для при 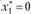). Таким образом, оптимальная стратегия имеет вид (0; 0; 4).

Таблица 3.16