| l | f1(l) | f2(l) | f3(l) | ||||||||
| x1 = 0 | x1 = 1 | x1 = 2 | x2 = 0 | x2 = 1 | x2 = 2 | x3 = 0 | x3 = 1 | x3 = 2 | x3 = 3 | x3 = 4 | |
| 0 | 0 | 0 | |||||||||
| 1 | 0 | 0 | |||||||||
| 2 | 0 | 0 | |||||||||
| 3 | 0 | 0 | -4 | ||||||||
| 4 | 0 | 3 | 0 | -4 | |||||||
| 5 | 0 | 3 | 0 | -4 | |||||||
| 6 | 0 | 3 | 0 | -4 | -8 | ||||||
| 7 | 0 | 3 | 0 | -1 | -8 | ||||||
| 8 | 0 | 3 | 12 | 0 | -1 | -8 | 12 | 6 | 27 | 81 | 192* |
Рассмотрим далее ряд основных понятий, связанных с имитационным моделированием. Во всех рассматриваемых выше оптимизационных моделях, так или иначе, предполагалась возможность использования аналитических методов решения, однако для многих задач анализа и управления в экономике такой возможности не существует. Если изучаемые процессы имеют явно нелинейный характер и при этом осложнены разного рода вероятностными характеристиками, то о практически полезном аналитическом решении не может быть и речи. В этих случаях могут быть применены методы машинной имитации, т.е. методы экспериментального изучения социально-экономических систем с помощью ЭВМ. Машинная имитация применяется тогда, когда реальный экономический эксперимент по каким-либо причинам невозможен, и тогда имитация выступает в качестве замены реального эксперимента либо в качестве предварительного этапа, позволяющего принять более обоснованное решение о проведении такого эксперимента.
При машинной имитации формируется так называемая имитационная система, в которую входят имитационная модель, имитирующая исследуемый процесс, и набор алгоритмов и программ, предназначенных как для обеспечения диалога человека и ЭВМ (внутреннее математическое обеспечение), так и для решения задач типа ввода и вывода информации, формирования базы данных и т.д. (внешнее математическое обеспечение). Имитационная модель при этом сама является своего рода программой для ЭВМ. Практическое применение этой модели заключается в наблюдении за результатами весьма многовариантных расчетов по такой программе при различных задаваемых значениях вводимых экзогенных переменных. В процессе анализа этих результатов могут быть сделаны выводы о поведении системы без ее построения, если эта система только проектируется, без вмешательства в ее функционирование, если это действующая система, и без ее разрушения, если целью эксперимента является определение пределов воздействия на систему. Таким образом, могут быть достигнуты цели экономико-математического моделирования в тех случаях, когда аналитическое решение невозможно.
Процесс последовательной разработки имитационной модели начинается с создания простой модели, которая затем постепенно усложняется в соответствии с предъявляемыми решаемой проблемой требованиями. В каждом цикле имитационного моделирования можно выделить следующие этапы.
1. Формирование проблемы: описание исследуемой проблемы и определение целей исследования.
2. Разработка модели: логико-математическое описание моделируемой системы в соответствии с формулировкой проблемы.
3. Подготовка данных: идентификация, спецификация и сбор данных.
4. Трансляция модели: перевод модели со специальных имитационных языков, используемых на этапе 2 (СИМУЛА, СЛАМ и др.), на язык, приемлемый для используемой ЭВМ.
5. Верификация: установление правильности машинных программ.
6. Валидация: оценка требуемой точности и адекватности имитационной модели.
7. Планирование: определение условий проведения машинного эксперимента с имитационной моделью.
8. Экспериментирование: многократный прогон имитационной модели на ЭВМ для получения требуемой информации.
9. Анализ результатов: изучение результатов имитационного эксперимента для подготовки выводов и рекомендаций по решению проблемы.
10. Реализация и документирование: реализация рекомендаций, полученных на основе имитации, и составление документации по модели и ее использованию.
Имитационные модели часто используются для принятия решений в условиях риска (напомним, что в классе моделей принятия решений в условиях риска мы можем сделать предположения об исходах случайных параметров и вероятностях наступления каждого возможного состояния).
В этом случае в основе имитационного моделирования лежит метод статистического моделирования (метод Монте-Карло). Этот метод позволяет воспроизводить на компьютере случайные величины (с.в.) с заданными законами распределения. Так как отдельные реализации этих с.в. получены искусственно, то их реализации называют псевдослучайными числами. Процедуры получения псевдослучайных чисел называют генераторами (датчиками) псевдослучайных чисел.
Например, при проведении имитационных экспериментов в среде MS Excel (при использовании стандартных офисных средств) могут быть использованы встроенные датчики, генерирующие семь типов распределений: равномерное, Пуассона, нормальное, Бернулли, биномиальное, модельное и дискретное (опции Инструменты анализа/Генерация случайных чисел надстройки Пакет анализа).
Примеры имитационного моделирования систем управления запасами и массового обслуживания средствами MS Excel приведены, например, в литературе.
Обязательным элементом "моделирующего алгоритма" в реальных имитационных экспериментах является оценка точности результатов, полученных методом статистических испытаний.
Для любых законов распределения случайной величины с помощью неравенства Чебышева можно получить верхнюю оценку ошибки, т.е. ошибка не может быть больше результата, полученного методом статистических испытаний. При нормальном законе распределения результата, полученного методом статистических испытаний, ошибка будет определяться неравенством
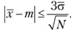
Это неравенство дает точную оценку возможной ошибки. Таким образом, для определения ошибки результата моделирования случайной величины необходимо вначале по данным N испытаний вычислить среднее статистическое 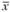 , статистическое среднеквадратичное отклонение
, статистическое среднеквадратичное отклонение 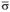 и лишь затем оценить ошибку результата на основе приведенного неравенства. Если ошибка окажется больше приемлемой, то потребуется увеличение числа испытаний N.
и лишь затем оценить ошибку результата на основе приведенного неравенства. Если ошибка окажется больше приемлемой, то потребуется увеличение числа испытаний N.
Так, имитируя работу одноканальной СМО с отказами, надо получить N раз реализации хi соответственно с.в. длительности интервалов между отдельными поступлениями требований и с.в. длительности интервалов по обслуживанию требований и с помощью "моделирующего алгоритма" зафиксировать число отказов в такой системе. При большом числе испытаний N получим, например, достаточно точную статистическую оценку вероятности отказа в обслуживании (конечно, предварительно проводится статистическая оценка гипотез о характере законов распределения входного потока требований и длительности интервалов обслуживания).
Модели сетевого планирования и управления
Во многих областях экономики, технологии, проектирования, строительства, научных исследований важное значение имеют задачи оптимизации распределения ресурсов (трудовых, финансовых и др.). Особую значимость приобретают эти задачи в условиях реализации новых проектов, когда выполняется огромное количество взаимозаменяемых операций, в работу вовлекается множество работников, предприятий, организаций, так как в этих случаях управление работами усложняется новизной разработки, трудностью точного определения сроков и затрат ресурсов на том или ином этапе. Высокоэффективными инструментами для решения таких задач являются сетевые методы и модели.
Основные понятия сетевого моделирования
Сетевой моделью (другие названия: сетевой график, сеть) называется экономико-математическая модель, отражающая комплекс работ (операций) и событий, связанных с реализацией некоторого проекта (научно-исследовательского, производственного и др.), в их логической и технологической последовательности и связи. Анализ сетевой модели, представленной в графической или табличной (матричной) форме, позволяет, во-первых, более четко выявить взаимосвязи этапов реализации проекта и, во-вторых, определить наиболее оптимальный порядок выполнения этих этапов в целях, например, сокращения сроков выполнения всего комплекса работ. Таким образом, методы сетевого моделирования можно отнести к методам принятия оптимальных решений.
Математический аппарат сетевых моделей базируется на теории графов. Графом называется совокупность двух конечных множеств: множества точек, которые называются вершинами, и множества пар вершин, которые называются ребрами. Представление о графе можно получить, если рассмотреть некоторый геометрический многогранник, например куб; в кубе можно выделить два конечных множества, состоящих соответственно из восьми вершин и двенадцати ребер.
Если рассматриваемые пары вершин являются упорядоченными, т.е. на каждом ребре задается направление, то граф называется ориентированным; в противном случае - неориентированным. Последовательность неповторяющихся ребер, ведущая от некоторой вершины к другой, образует путь. Граф называется связным, если для любых двух его вершин существует путь, их соединяющий; в противном случае граф называется несвязным. В экономике чаще всего используется два вида графов: дерево и сеть. Дерево представляет собой связный граф без циклов, имеющий исходную вершину (корень) и крайние вершины; пути от исходной вершины к крайним вершинам называются ветвями. Сеть - это ориентированный конечный связный граф, имеющий начальную вершину (источник) и конечную вершину (сток). Таким образом, сетевая модель представляет собой граф вида "сеть".
В экономических исследованиях сетевые модели возникают при моделировании экономических систем и процессов методами сетевого планирования и управления (СНУ).
Объектом управления в системах сетевого планирования и управления являются коллективы исполнителей, располагающие определенными ресурсами и выполняющие заданный комплекс операций, который призван обеспечить достижение намеченной цели, например разработку нового изделия, строительство объекта и т.п.
Основой СНУ служит сетевая модель (СМ), в которой моделируется совокупность взаимосвязанных работ и событий, отображающих процесс достижения определенной цели. Она может быть представлена в виде графика или таблицы.
Основными понятиями СМ являются следующие: работа, событие, путь. На рис. 3.7 графически представлена СМ, состоящая из 5 событий (кружочки) и 6 работ (стрелки); продолжительность выполнения работ в некоторых единицах времени указана над стрелками.
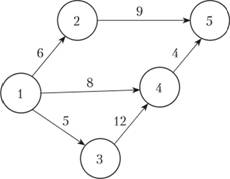
Рис. 3.7. Сетевая модель
Работа характеризует материальное действие, требующее использования ресурсов, или логическое, требующее лишь взаимосвязи событий. При графическом распределении работа изображается стрелкой, которая соединяет два события. Ома обозначается парой заключенных в скобки чисел (i,j), где i - номер события, из которого работа выходит, a j - номер события, в которое она входит. Работа не может начаться раньше, чем свершится событие, из которого она выходит. Каждая работа имеет определенную продолжительность t(i,j). Например, запись t(2, 5) = 9 означает, что работа (2, 5) имеет продолжительность 9 единиц времени (см. рис. 3.7). К работам относятся также такие процессы, которые не требуют ни ресурсов, ни времени выполнения. Они заключаются в установлении логической взаимосвязи работ и показывают, что одна из них непосредственно зависит от другой и не может выполняться, прежде чем эта другая будет завершена; такие работы называются фиктивными и на графике изображаются пунктирными стрелками.
Событиями называются результаты выполнения одной или нескольких работ. Они не имеют протяженности во времени. Событие свершается в тот момент, когда оканчивается последняя из работ, входящая в него. События обозначаются одним числом и при графическом представлении СМ изображаются кружком (или иной геометрической фигурой), внутри которого проставляется его порядковый номер (i = 1, 2,... N). В СМ имеется начальное событие (с номером 1), из которого работы только выходят, и конечное событие (с номером N), в которое работы только входят.
Путь в СМ - это цепочка следующих друг за другом работ, соединяющих начальную и конечную вершины, например, в приведенной на рис. 3.7 модели путями являются L1 = (1, 2, 5), L2 = (1, 4, 5) и др. Продолжительность пути определяется суммой продолжительностей составляющих его работ. Путь, имеющий максимальную длину, называют критическим и обозначают Lкр, а его продолжительность - tкр Работы, принадлежащие критическому пути, называются критическими. Их несвоевременное выполнение ведет к срыву сроков всего комплекса работ.
Дата: 2019-02-25, просмотров: 335.