Целочисленным (иногда его называют также дискретным) программированием называется раздел математического программирования, изучающий экстремальные задачи, в которых на искомые переменные накладывается условие целочисленности, а область допустимых решений конечна. Изучение этого раздела в курсе "Экономико-математические методы и прикладные модели" вызывается тем, что огромное количество экономических задач носит дискретный, чаще всего целочисленный характер, что связано, как правило, с физической неделимостью многих элементов расчета: например, нельзя построить два с половиной завода, купить полтора автомобиля и т.д. В ряде случаев такие задачи решаются обычными методами, например симплексным методом, с последующим округлением до целых чисел. Однако такой подход оправдан, когда отдельная единица составляет очень малую часть всего объема (например, товарных запасов); в противном случае он может внести значительные искажения в действительно оптимальное решение. Поэтому разработаны специальные методы решения целочисленных задач, среди которых можно выделить два направления: методы отсечения (отсекающих плоскостей) и комбинаторные методы.

Метод отсекающих плоскостей состоит в построении дополнительных ограничений и применении двойственного симплексного метода. Представление о комбинаторных методах дает широко используемый на практике метод ветвей и границ.

Рассмотрим более подробно один из методов отсекающих плоскостей, известный как метод Гомори. Метод Гомори для линейных задач целочисленного программирования основан на понятии конгруэнтности действительных чисел. Любое действительное число можно представить в виде суммы его целой и дробной частей: х = [x] + {x} где квадратные скобки означают целую часть, а фигурные - дробную. Например, 7,5 = [7,5] + {7,5} = 7 + 0,5. Неотрицательные числа (для простоты мы будем рассматривать только их) называются конгруэнтными, если равны их дробные части. Если обозначать конгруэнтность чисел символом " ≡", то, например, 7,5 ≡ 0,5; 6,3 ≡ 2,3; в частности, все целые числа конгруэнтны нулю, поэтому условие целочисленности переменной х можно записать: х_i = 0.

По методу Гомори первый этап решения целочисленных задач не отличается от обычного расчета по симплексному алгоритму. Если среди значений переменных в оптимальном плане есть дробные, то составляется дополнительное ограничение, отсекающее дробную часть решения, но оставляющее в силе все прочие условия, которым должен удовлетворять оптимальный план. Это дополнительное ограничение присоединяется к исходным ограничениям задачи, и вновь применяется процедура симплексного метода. Алгоритм Гомори позволяет прийти к оптимальному целочисленному решению за конечное число шагов.

Пример 3.6. Пусть для приобретения оборудования, размещаемого на производственной площади 38 м², фирма выделяет 20 млн руб. Имеются единицы оборудования двух типов: типа А стоимостью 5 млн руб., требующее производственную площадь 8 м² и имеющее производительность 7 тыс. ед. продукции за смену, и типа Б - стоимостью 2 млн руб., занимающее площадь 4 м² и дающее за смену 3 тыс. ед. продукции. Требуется рассчитать оптимальный вариант приобретения оборудования, обеспечивающий максимум производительности участка.

Решение. Сформулируем экономико-математическую модель задачи. Пусть х₁, х₂ - количество приобретаемых машин типа А и типа Б соответственно. Тогда целевая функция задачи будет иметь вид

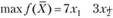
при ограничениях:

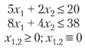
Сформулирована задача линейного целочисленного программирования.

Введем дополнительные переменные х₄, с помощью которых исходные неравенства преобразуются в равенства:

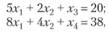
из которых следует, что переменные х₁, х₂ могут принимать только неотрицательные целочисленные значения. Фрагмент симплексной таблицы на последней итерации (без учета целочисленности) приведен в табл. 3.15.

Таблица 3.15

Базисные переменные	План	x1	x2	x3	x4
x1	1	1	0	1	-0,5
x2	7,5	0	1	-2	1,26
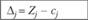
	29,5	0	0	1	0,25

Отсюда видно, что в оптимальном плане х₁, = 1; х₂ = 7,5 и максимум целевой функции равен

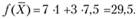
Для нецелочисленной переменной х₂ составляем из приведенной симплексной табл. 3.15 уравнение:

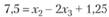
откуда

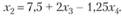
Так как х₂ - целое число, то целой должна быть и правая часть последнего уравнения ("=" - символ конгруэнтности):

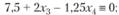
отсюда можно получить, что

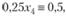
т.е. выражение 0,25х₄ может быть равно 0,5, или 1,5, или 2,5 и т.д. Следовательно, появляется дополнительное ограничение: 0,25х₄ > 0,5, которое путем ввода дополнительной неотрицательной целочисленной переменной х₅ преобразуется в равенство, так что система ограничений исходной задачи в каноническом виде содержит три уравнения:

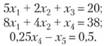
Повторив процесс решения симплексным методом для данной расширенной системы ограничений, получим новый оптимальный план, в котором переменные, входящие в базис, принимают целые значения: х₁ = 2; х₂ = 5; х ₄ = 2. Таким образом, приобретение двух машин типа А и пяти машин типа Б обеспечивает максимум производительности участка, равный 29 тыс. ед. продукции в смену. Заметим, что если бы в качестве плана был выбран вариант, получаемый в результате округления первоначального решения задачи симплексным методом (x₁ = 1; x₂ = 7), то суммарная производительность была бы равна лишь 28 тыс. ед. продукции.

Рассмотрим далее ряд специальных оптимизационных задач, сводящихся к задачам линейного целочисленного программирования. Одной из таких задач является задача о назначениях, с помощью которой можно получить ответ на вопросы типа: как распределить рабочих по станкам, чтобы общая выработка была наибольшей или затраты на заработную плату наименьшими; как наилучшим образом распределить экипажи самолетов; как назначить людей на различные должности (отсюда и название задачи) и т.д.

Математически такие задачи относятся к тому же типу распределительных задач, что и рассмотренная в параграфе 3.2 транспортная задача, с той особенностью, что в них объемы наличных и требующихся ресурсов для выполнения каждой работы равны единице (a_i = b_j = 1), а все переменные x_ij: либо равны единице, если i-й работник назначен на j-ю работу, либо равны нулю в других случаях. Исходные данные задачи о назначениях группируются в таблице, которая называется матрицей оценок, а результаты - в матрице назначений.

Задача о назначениях в общем виде может быть сформулирована следующим образом. Имеется п работников, которые могут выполнять п работ, причем использование г-го работника на j-й работе, например, приносит доход с_ij. Требуется поручить каждому из работников выполнение одной вполне определенной работы, чтобы максимизировать в данном случае суммарный доход.

Введем переменные:

Задача состоит в том, чтобы найти распределение X = (Xjj) работников по работам (т.е. найти матрицу назначений), которое максимизирует целевую функцию

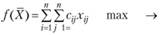(3.22)

при ограничениях

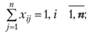(3.23)

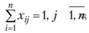(3.24)

причем x_ij равно либо 0, либо 1 (так называемые булевы переменные) для всех i,j = i,n.

Ограничения (3.23) отражают условие того, что за каждым работником может быть закреплена только одна работа, а ограничения (3.24) означают, что для выполнения каждой работы может быть выделен только один работник.

Если в задаче о назначениях элементы матрицы оценок представляют собой, например, время выполнения каждым работником любой из работ, то целевая функция этой задачи будет минимизироваться. Следует заметить также, что при решении задачи о назначениях часто используются алгоритмы и методы решения транспортных задач, в частности метод потенциалов.

Другой задачей подобного рода является задача о коммивояжере, которая может быть сформулирована следующим образом. Имеется п городов, пронумерованных числами от 1 до п. Коммивояжер, выезжая из города 1, должен побывать в каждом городе ровно один раз и вернуться в исходный пункт. Пусть известны расстояния с_ij между городами (i,j = 1,n; i j). Требуется найти самый короткий маршрут.

Введем переменные:

Требование однократного въезда в города и выезда из них запишется в виде следующих ограничений:

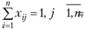(3.25)

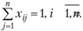
Однако ограничения (3.25) полностью не определяют допустимые маршруты, так как не исключают возможности разрыва пути, т.е. появления нескольких не связанных между собой подмаршрутов для части городов. Поэтому следует ввести дополнительно п переменных и_i (и_i (i = 1, п), принимающих только целые неотрицательные значения, и записать для них специальные ограничения:

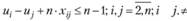(3.26)

Общее число таких ограничений равно (п - 1) · (n - 2), и они, не исключая допустимый маршрут, исключают возможность существования подмаршрутов.

Таким образом, задача о коммивояжере состоит в минимизации целевой функции:

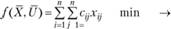(3.27)

при условиях (3.25), (3.26), где переменные Ху, и, принимают только неотрицательные целые значения.

К задачам целочисленного программирования приводят также многие оптимальные задачи теории расписаний, в которой рассматриваются методы оптимизации оперативно-календарного планирования. В качестве примера таких задач можно привести задачу определения оптимальной очередности обработки изделий на различных станках или других рабочих местах, задачу составления программы "диспетчер" для управления работой ЭВМ в мультипрограммном режиме и др.