Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Для взаимодвойственных ЗЛП имеет место один из взаимоисключающих случаев.

1. В прямой и двойственной задачах имеются оптимальные решения, при этом значения целевых функций на оптимальных решениях совпадают: max f(X) = min g(Y).

2. В прямой задаче допустимое множество не пусто, а целевая функция на этом множестве не ограничена сверху. При этом у двойственной задачи будет пустое допустимое множество.

3. В двойственной задаче допустимое множество не пусто, а целевая функция на этом множестве не ограничена снизу. При этом у прямой задачи допустимое множество оказывается пустым.

4. Обе из рассматриваемых задач имеют пустые допустимые множества.

Вторая теорема двойственности (теорема о дополняющей нежесткости)

Пусть 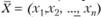- допустимое решение прямой задачи (3.1)-(3.3), а 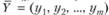- допустимое решение двойственной задачи (3.4)-(3.6). Для того чтобы они были оптимальными решениями соответствующих взаимодвойсгвенных задач (3.1)-(3.3) и (3.4)-(3.6), необходимо и достаточно, чтобы выполнялись следующие соотношения:

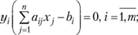(3.7)

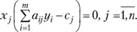(3.8)

Условия (3.7) и (3.8) позволяют, зная оптимальное решение одной из взаимодвойственных задач, найти оптимальное решение другой задачи.

Рассмотрим еще одну теорему, выводы которой будут использованы в дальнейшем.

Теорема об оценках (третья теорема двойственности)

Значения переменных y_i в оптимальном решении двойственной задачи представляют собой оценки влияния свободных членов b_i системы ограничений - неравенств прямой задачи на величину целевой функции этой задачи:

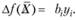(3.9)

Решая ЗЛП симплексным методом, мы одновременно решаем двойственную ЗЛП. Значения переменных двойственной задачи г/, в оптимальном плане называют, как выше уже отмечено, объективно обусловленными, или двойственными оценками.

Рассмотрим экономическую интерпретацию двойственной задачи на следующем примере.

Пример 3.1 (задача оптимального использования ресурсов). Пусть для выпуска четырех видов продукции Р₁, Р₂, Р₃, Р₄ на предприятии используют три вида сырья S₁, S₂ и S₃. Объемы выделенного сырья, нормы расхода сырья и прибыль на единицу продукции при изготовлении каждого вида продукции приведены в табл. 3.1. Требуется определить план выпуска продукции, обеспечивающий наибольшую прибыль.

Решение. Составим экономико-математическую модель задачи оптимального использования ресурсов на максимум прибыли. В качестве неизвестных примем объем выпуска продукции j-го вида x_j (j = 1, 2, 3, 4).

Таблица 3.1

Исходные данные

Вид сырья	Запасы сырья	Вид продукции
		Р1	Р2	Р3	Р4
S1	35	4	2	2	3
S2	30	1	1	2	3
S3	40	3	1	2	1
Прибыль		14	10	14	11

Модель задачи по критерию "максимум прибыли":

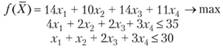
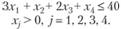
Теперь сформулируем двойственную задачу. Пусть некая организация решила закупить все ресурсы рассматриваемого предприятия. При этом необходимо установить оптимальную цену на приобретаемые ресурсы у₁, у₂, y₃ исходя из следующих объективных условий:

1) покупающая организация старается минимизировать общую стоимость ресурсов;

2) за каждый вид ресурсов надо уплатить не менее той суммы, которую хозяйство может выручить при переработке сырья в готовую продукцию.

Согласно первому условию общая стоимость сырья выразится величиной 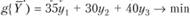. Согласно второму требованию вводятся ограничения: на единицу первого вида продукции расходуются четыре единицы первого ресурса ценой y₁, одна единица второго ресурса ценой у₂ и три единицы третьего ресурса ценой у₃. Стоимость всех ресурсов, расходуемых на производство единицы первого вида продукции, равна 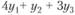и должна составлять не менее 14, т.е.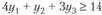

В результате аналогичных рассуждений относительно производства второго, третьего и четвертого видов продукции получаем систему неравенств:

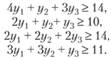
По экономическому смыслу цены неотрицательные:

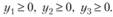
Получили симметричную пару взаимодвойственных задач. В результате решения данной задачи симплексным методом получен оптимальный план 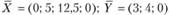. На рис. 3.1 приведен результат решения задачи с использованием надстройки Поиск решения Excel. Жирным шрифтом выделены оптимальные значения 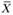и .

Экономический смысл первой теоремы двойственности следующий. План производства X и набор оценок ресурсов Y оказываются оптимальными тогда и только тогда, когда прибыль от реализации продукции, определенная при известных заранее ценах продукции с₁, с₂,..., с₃, равна затратам на ресурсы но "внутренним" (определяемым только из решения задачи) ценам ресурсов у₁, у_2,…,у_т. Для всех же других планов и 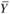обеих задач прибыль от продукции всегда меньше (или равна) стоимости затраченных ресурсов: 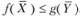, т.е. ценность всей выпущенной продукции не превосходит суммарной оценки имеющихся ресурсов. Значит, величина 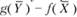характеризует производственные потери в зависимости от рассматриваемой производственной программы и выбранных оценок ресурсов.

Ячейки переменных

Ячейка Имя Окончательное значение Приведенная стоимость

Целевая функция

Коэффициент

Допустимое увеличение Допустимое уменьшение SBS1   0 -2 14

2

1Е+30 SCSI   5 0 10

4

0.666666667 SDS1   12,5 0 14

2

4 SES1   0 -10 11

10

1Е+30

Ограничения

Ячейка Имя Окончательное значение Теневая цена Ограничение Правая сторона

Допустимое увеличение

Допустимое уменьшение SFS3   35 3 35

25

5 SFS4   30 4 30

5

12.5 $Н$5   30 0 40

1Е+30

10                

Рис. 3.1. Отчет по устойчивости Microsoft Excel

Из первой теоремы двойственности следует, что при оптимальных производственной программе и векторе оценок ресурсов производственные потери равны нулю.

Экономический смысл первой теоремы двойственности можно интерпретировать и так: предприятию безразлично, производить ли продукцию по оптимальному плану 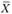и получить максимальную прибыль либо продать ресурсы по оптимальным ценам 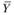и возместить от продажи равные ей минимальные затраты на ресурсы.

Из второй теоремы двойственности в данном случае следуют такие требования на оптимальную производственную программу 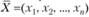и оптимальный вектор оценок :

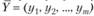если 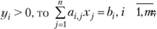(3.10)

если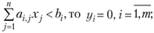

если 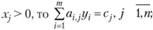(3.11)

если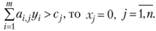

Условия (3.10) можно интерпретировать так: если оценка у_i, единицы ресурса г-го вида положительна, то при оптимальной производственной программе этот ресурс используется полностью; если же ресурс используется не полностью, то его оценка равна нулю.

Из условия (3.11) следует, что если j-й вид продукции вошел в оптимальный план, то он в оптимальных оценках не убыточен; если же j-й вид продукции убыточен, то он не войдет в план, не будет выпускаться.

Кроме нахождения оптимального решения должно быть обеспечено получение дополнительной информации о возможных изменениях решения при изменении параметров системы. Эту часть исследования обычно называют анализом модели на чувствительность. Он необходим, например, в тех случаях, когда некоторые характеристики исследуемой системы не поддаются точной оценке.

Экономико-математический анализ решений осуществляется в двух основных направлениях: в виде вариантных расчетов по моделям с сопоставлением различных вариантов плана и в виде анализа каждого из полученных решений с помощью двойственных оценок. Вариантные расчеты могут осуществляться при неизменной структуре самой модели (постоянном составе неизвестных, способов производства, ограничений задачи и одинаковом критерии оптимизации), но с изменением численной величины конкретных показателей модели. Вариантные расчеты могут проводиться также при варьировании элементов самой модели: изменении критерия оптимизации, добавлении новых ограничений на ресурсы или на способы производства их использования, расширения множества вариантов и т.д.

Одно из эффективных средств экономико-математического анализа - использование объективно обусловленных оценок оптимального плана. Такого рода анализ базируется на свойствах двойственных оценок. Выше мы установили общие математические свойства двойственных оценок для задач на оптимум любой экономической природы. Однако экономическая интерпретация этих оценок может быть совершенно различной для разных задач.

Перейдем к рассмотрению конкретных экономических свойств оценок y_i, оптимального плана. Сначала перечислим эти свойства, а затем проиллюстрируем их конкретными примерами.

Свойство 1. Оценки как мера дефицитности ресурсов и продукции.

Свойство 2. Оценки как мера влияния ограничений на функционал.

Свойство 3. Оценки как инструмент определения эффективности отдельных вариантов.

Свойство 4. Оценки как инструмент балансирования суммарных затрат и результатов.

Пример 3.2 (задача о планировании выпуска тканей). Пусть некоторая фабрика выпускает три вида тканей, причем суточное плановое задание составляет не менее 90 м тканей первого вида, 70 м - второго и 60 м - третьего. Суточные ресурсы следующие: 780 единиц производственного оборудования, 850 единиц сырья и 790 единиц электроэнергии, расход которых на один метр ткани представлен в табл. 3.2.

Таблица 3.2

Нормы расхода ресурсов

Ресурсы	Ткани
	I	II	III
Оборудование	2	3	4
Сырье	I	4	э
Электроэнергия	3	4	2

Цена за один метр ткани вида I равна 80 денежным единицам, II - 70 денежным единицам, III - 60 денежным единицам.

Необходимо определить, сколько метров ткани каждого вида следует выпустить, чтобы общая стоимость выпускаемой продукции была максимальной.

Решение. Составим модель задачи. Введем следующие обозначения. Неизвестными в задаче являются объемы выпуска ткани каждого вида:

x₁ - количество метров ткани вида I;

х₂ - количество метров ткани вида II;

х₃ - количество метров ткани вида III.

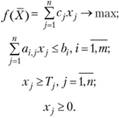
С учетом имеющихся данных модель примет вид:

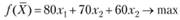
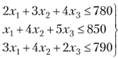Ограничение по ресурсам

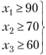Плановое задание

В результате решения задачи симплексным методом получен следующий оптимальный план: максимум общей стоимости продукции 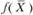= 19 075 ден. ед. достигается при

x₁ = 112,5 м - оптимальный объем выпуска ткани вида I;

x₂ = 70 м - оптимальный объем выпуска ткани вида II;

x₃ = 86,25 м - оптимальный объем выпуска ткани вида III.

Решение двойственной задачи получим с использованием теорем двойственности. Введем обозначения:

y₁ - двойственная оценка ресурса "оборудование";

y₂ - двойственная оценка ресурса "сырье";

y₃ - двойственная оценка ресурса "электроэнергия";

y₄ - двойственная оценка ткани вида I;

y₅ - двойственная оценка ткани вида II;

y₆ - двойственная оценка ткани вида III.

Модель двойственной задачи имеет вид:

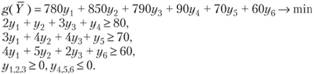
Из соотношений второй теоремы двойственности вытекают следующие условия:

для каждого ресурса:

если ;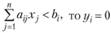

если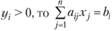

для задания по выпуску продукции:

если 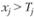, то ;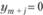

если 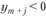, то 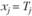. (3.12)

Для нашего примера в этих соотношениях т = 3 (количество типов ресурсов).

Подставим значения x₁ = 112,5, x₂ = 70 и x₃ = 86,25 в ограничения прямой задачи:

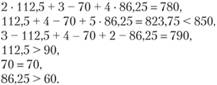
Суточные ресурсы по оборудованию и электроэнергии использованы полностью. Сырье используется не полностью, имеется остаток в размере 850 - 823,75 = 26,25 (кг). План выпуска по тканям вида I и III перевыполнен.

Из второй теоремы двойственности вытекает, что y₂, y₄ и y₆ равны нулю. Остается найти значения y₁, y₃ и y₅. Так как x₁, x₂ и x₃ - больше нуля, то все три ограничения двойственной задачи выполняются как равенства:

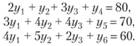
Учитывая, что 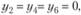имеем:

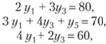
откуда .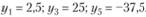

Подставив значения неизвестных в целевую функцию двойственной задачи, проверим, выполняется ли условие 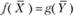для оптимального плана:

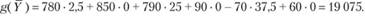
Условие первой теоремы двойственности выполняется, следовательно, рассмотренный план выпуска тканей и соответствующая ему система оценок ресурсов и продукции оптимальны.

Экономическое истолкование оценок есть интерпретация их общих экономико-математических свойств применительно к конкретному содержанию задачи. По условию (3.10) не использованный полностью в оптимальном плане ресурс получает нулевую оценку. Нулевая оценка ресурса свидетельствует о его недефицитности. Ресурс недефицитен не из-за его неограниченных запасов (они ограничены величиной b_i), а из-за невозможности его полного использования в оптимальном плане. Так как суммарный расход недефицитного ресурса меньше его общего количества, то план производства им не лимитируется. Данный ресурс не препятствует и дальше максимизировать целевую функцию .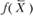

Ограничивают целевую функцию дефицитные ресурсы, в данном примере - оборудование и электроэнергия. Они полностью использованы в оптимальном плане. По условию (3.10) оценка таких ресурсов положительна (y₁ = 2,5; y₃ = 25). Рассмотрим теперь понятие дефицитности продукции. По условию (3.12) нулевую оценку (y₄ = 0, y₆ = 0) получает продукция, задания по выпуску которой в оптимальном плане перевыполняются. Очевидно, перевыполнение плана целесообразно по выгодной продукции (ткани I и III видов), т.е. такой, производство которой способствует достижению максимума критерия оптимальности. Размеры производства такой выгодной продукции определяются не величиной задания на выпуск (T_j) (в оптимальном плане они перекрыты), а ограниченностью дефицитных ресурсов. Эту продукцию выпускают как можно больше, пока хватит ресурсов. Выпуск выгодной продукции лимитируется не только фактом ограниченности дефицитных ресурсов, но и тем, что часть дефицитных ресурсов требуется выделить на обеспечение выпуска невыгодной продукции в соответствии с плановыми заданиями. По условию (3.12) отрицательную оценку (y₅ = -37,5) получает продукция, задания, по выпуску которой, не перевыполняются. Так как по условию задачи (X_j > T_j) плановые задания должны быть обязательно выполнены, то продукция делится на выгодную (виды 1 и III ткани) и невыгодную (вид II ткани).

Если в ограничение двойственной задачи, относящееся к виду II ткани,

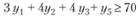
подставить полученные значения двойственных оценок, то получаем

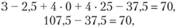
т.е. стоимость ресурсов, затраченных на один метр ткани вида II, составляет 107,5 денежной единицы, и это на 37,5 денежной единицы больше цены одного метра ткани этого вида. Таким образом, вид II ткани убыточен для фабрики: на каждом выпущенном метре ткани этого вида фабрика теряет 37,5 денежной единицы.

В соответствии с критерием оптимальности плана, в зависимости от того перевыполняется план выпуска или нет, выпуск ткани вида II поглощает часть дефицитных ресурсов, чем сдерживает рост выпуска выгодной продукции, а тем самым и рост целевой функции.

Оценка ресурса показывает, насколько изменится критерий оптимальности при изменении количества данного ресурса на единицу. Для недефицитного ресурса оценка равна нулю, поэтому изменение его величины не повлияет на критерий оптимальности. Дефицитность ресурса измеряется вкладом единицы ресурса в изменение целевой функции.

Влияние ограничений по выпуску продукции на критерий оптимальности противоположно влиянию ограничений по ресурсам. Если продукция невыгодна (вид II ткани, y₅ = -37,5), то увеличение плановых заданий по ее выпуску ведет к уменьшению выпуска выгодной продукции и ухудшает план. Наоборот, уменьшение плановых заданий по невыгодной продукции позволяет снизить ее выпуск, перебросить сэкономленные ресурсы на дополнительный сверхплановый выпуск выгодных видов продукции, что увеличивает значение целевой функции. Изменение плановых заданий по выгодной продукции не изменяет значения целевой функции.

Перейдем к анализу модели на чувствительность.

Пример 3.3. На основании информации, приведенной в табл. 3.3, составить план производства, максимизирующий объем прибыли.

Таблица 3.3

Ресурсы	Затраты ресурсов на единицу продукции		Наличие ресурсов
	А	А
Труд	2	4	2000
Сырье	4	1	1400
Оборудование	2	1	800
Прибыль на единицу продукции	40	60

Решение. Экономико-математическая модель задачи будет иметь вид:

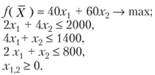
В результате решения задачи симплексным методом был получен следующий оптимальный план:

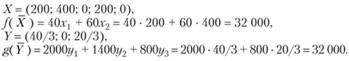
Соответствующий отчет об устойчивости решения представлен на рис. 3.2.

Ячейки переменных
Ячейка	Имя	Окончательное значение	Приведенная стоимость	Целевая функция Коэффициент		Допустимое увеличение	Допустимое уменьшение
$A$2		200	0	40	80		10
$B$2		400	0	60	20		40
Ограничения
Ячейка	Имя	Окончательное значение	Теневая цена	Ограничение Правая сторона	Допустимое увеличение		Допустимое уменьшение
$С$4		2000	13.3333333337	2000	1200		600
$С$5		1200	0	1400	1E+30		200
$С$6		800	6.6666666667	800	85.71428571		300

Рис. 3.2. Отчет об устойчивости

После того как оптимальное решение получено, выявляется его чувствительность к определенным изменениям исходной модели. В нашей задаче, например, может представить интерес то, как повлияет на оптимальное решение изменение запасов сырья и изменение прибыли от единицы продукции. В связи с этим логично выяснить.

1. Увеличение объемов какого вида ресурсов наиболее выгодно?

2. Насколько можно увеличить запас сырья для улучшения полученного оптимального значения целевой функции?

3. Каков диапазон изменения того или иного коэффициента целевой функции, при котором не происходит изменения оптимального решения?

4. Целесообразность включения в план новых изделий.

Постараемся последовательно ответить на все поставленные вопросы.

1. Ценность ресурсов. В примере 3.3 объективно обусловленные оценки ресурса "труд" равны 40/3 (y₁ = 40/3), "сырье" - 0 (y₂ = 0), "оборудование" - 20/3 (y₃ = 20/3).

Дефицитный ресурс, полностью используемый в оптимальном плане ( 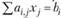), имеет положительную оценку (y_i > 0); недефицитный, не полностью используемый ресурс (для которого 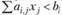), имеет нулевую оценку (y_i = 0). В примере "сырье" не является дефицитным ресурсом:

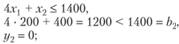
а "труд" и "оборудование" - дефицитные ресурсы:

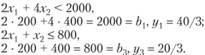
Чем выше величина оценки y_i, тем острее дефицитность i-го ресурса. В примере "труд" более дефицитен, чем "оборудование": 40/3 > 20/3. Наиболее выгодно увеличение объемов ресурса труда.

Заметим, что ценность различных видов сырья нельзя отождествлять с действительными ценами, по которым осуществляется его закупка. В данном случае речь идет о некоторой мере, имеющей экономическую природу, которая характеризует ценность сырья только относительно полученного оптимального решения.

2. Чувствительность решения к изменению запасов сырья. Предположим, что запас сырья ресурса "труд" изменился на 12 единиц, т.е. теперь он составляет 2000 + 12 = 2012 единиц.

Из теоремы об оценках 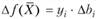известно, что колебание величины b_j приводит к увеличению или уменьшению 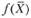. Оно определяется величиной y_i, в случае, когда при изменении величин b_j значения переменных y_i, в оптимальном плане соответствующей двойственной задачи, остаются неизменными. Поэтому необходимо найти такие интервалы изменения каждого из свободных членов системы ограничений исходной ЗЛП, в которых оптимальный план двойственной задачи не менялся бы.

Для двойственных оценок оптимального плана весьма существенное значение имеет их предельный характер.

Точной мерой влияния ограничений на функционал оценки являются лишь при малом приращении ограничения.

Известно, что оценки не меняют своей величины, если не меняется набор векторов, входящих в базис оптимального плана, тогда как интенсивность этих векторов (значения неизвестных) в плане могут меняться.

Рассмотрим модель исходной задачи (3.1)-(3.3) в матричной форме:

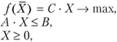
где X = (x₁, x₂,..., x_n) - вектор неизвестных;

С = (с₁, с₂,..., с_n) - вектор коэффициентов при неизвестных в целевой функции;

В = (b₁, b₂, ..., b_m) - вектор свободных членов ограничений исходной задачи;

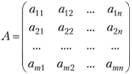- матрица коэффициентов в системе ограничений.

Приведем задачу к канонической форме, введем т дополнительных переменных. Задача примет вид:

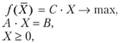
где вектор неизвестных переменных X будет теперь иметь размерность п + т. Размерность матрицы А также изменится и будет равна т · (п + т).

Пусть известен оптимальный план. Разобьем вектор X на два подвектора: 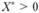и 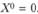. В первый включены неизвестные, вошедшие в базис оптимального решения (т.е. ненулевые в оптимальном плане). Соответственно матрицу А разобьем на две подматрицы: А* (размерность т x т) и A⁰ (размерность т x n). Первую из них сформируют т.е. столбцы матрицы А, которые соответствуют ненулевым неизвестным в оптимальном плане. Тогда 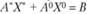. Так как 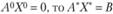. Умножив обе части последнего равенства на матрицу, обратную матрице А, получим 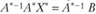. Так как 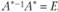, где Е - единичная матрица, то 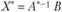. Обозначим 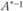через D, тогда .

Матрица D характеризует влияние ресурсов на величину выпуска продукции X. Изменим размер выделяемых ресурсов, т.е. дадим приращение 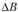вектору В. Тогда

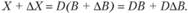
С учетом X = DB можно записать:

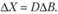
Это соотношение определяет величину структурных сдвигов в выпуске продукции при изменении ограничений исходной задачи. Из соотношений второй теоремы двойственности видно, что двойственные оценки (переменные двойственные задачи) тесным образом связаны с оптимальным планом простой задачи. Всякое изменение исходных данных прямой задачи может оказать влияние как на ее оптимальный план ( 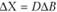), так и на систему оптимальных двойственных оценок. Поэтому, чтобы проводить экономический анализ с использованием двойственных оценок, нужно знать их интервал устойчивости.

Второе свойство двойственных оценок означает, что изменение значений величины b_i приводит к увеличению или уменьшению 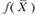. Это изменение, как выше уже отмечено, определяется величиной y_i; и может быть определено лишь тогда, когда при изменении величин b_i значения переменных y_i; в оптимальном плане соответствующей двойственной задачи остаются неизменными. Поэтому необходимо определить такие интервалы изменения каждого из свободных членов системы линейных уравнений АХ = В, в которых оптимальный план двойственной задачи не меняется. Это имеет место тогда, когда среди компонент вектора X = DB нет отрицательных.

Исходя из этого, получаем следующие оценки нижних и верхних пределов устойчивости двойственных оценок при изменении каждого ограничения в отдельности. Пределы уменьшения (нижняя граница) определяются по тем х_k(k = 1, ..., т), для которых соответствующие d_kj> 0:

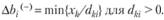(3.13)

Пределы увеличения (верхняя граница) определяются по тем х_k, для которых d_kj< 0:

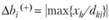для 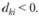(3.14)

Ослабление какого-либо i-го ограничения приводит к тому, что с определенного момента оказывается возможным изменить структуру (набор векторов) в базисе плана, что ведет к скачкообразному уменьшению величины оценки. Так продолжается до тех пор, пока i-й ресурс вообще перестанет быть дефицитным и его оценка обратится в нуль.

Определим интервалы устойчивости двойственных оценок в примере 3.3. Матрица А имеет вид

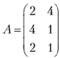
После приведения задачи к канонической форме матрица А примет следующий вид:

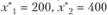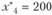С ненулевыми значениями в оптимальный план вошли и , следовательно, матрица А * будет составлена из первого, второго и четвертого столбцов матрицы А:

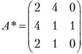
Для вычисления интервалов устойчивости необходимо найти матрицу 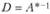(правила вычисления обратной матрицы приведены в главе 2.

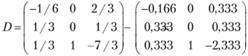
При вычислении интервалов устойчивости по формулам (3.13) и (3.14) примем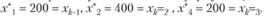

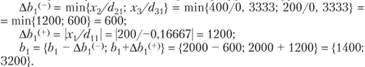
Интервалы устойчивости первого ресурса - "труд":

При изменении запасов ресурса "труд" в пределах от 1400 до 3200 единиц двойственная оценка его не изменится.

Интервалы устойчивости второго ресурса - "сырье":

этот ресурс в оптимальном плане используется не полностью и поэтому не имеет верхней границы интервалов устойчивости:

нижняя граница определяется следующим образом:

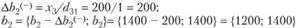
Интервалы устойчивости третьего ресурса - "оборудование":

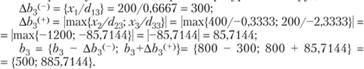
В нашем примере определим величину изменения объема прибыли от реализации продукции при увеличении ресурса "труд" на 12 единиц. Эти изменения находятся в интервалах устойчивости двойственных оценок, поэтому можно воспользоваться теоремой об оценках:

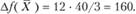
Объем прибыли увеличится на 160 единиц.

Такой же ответ мы получили бы, если бы решили симплексным методом задачу с новыми ограничениями по ресурсу "труд". Новый оптимальный план:

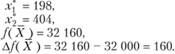
Структурных сдвигов в программе не произошло, но значения переменных в плане изменились: продукции вида Л может быть выпущено на 2 единицы меньше, а продукции вида Б - на 4 больше. Значение целевой функции при новых ограничениях увеличится на 160 единиц.

3. Чувствительность решения к изменению коэффициентов целевой функции. Так как любые изменения коэффициентов целевой функции оказывают влияние на оптимальность полученного ранее решения, то наша цель - найти такие диапазоны изменения коэффициентов в целевой функции (рассматривая каждый из коэффициентов отдельно), при которых оптимальные значения переменных остаются неизменными. Допустимые диапазоны изменения коэффициентов в целевой функции определятся из соотношений:

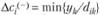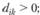
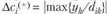для

для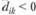

Используя эти соотношения в рассматриваемой задаче, получим для первого коэффициента целевой функции:

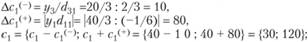
для второго коэффициента:

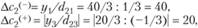
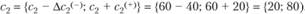
Таким образом, найденный оптимальный план выпуска продукции не будет меняться при изменении прибыли на единицу продукции А в диапазоне от 30 до 120 и прибыли на единицу второй продукции Б в диапазоне от 20 до 80.

4. Целесообразность включения в план новых изделий. Пусть в рассматриваемой нами задаче предприятию были предложены на выбор три новых изделия, за счет которых можно было бы расширить номенклатуру выпускаемой продукции при тех же запасах ресурсов. Нормы затрат ресурсов и прибыль от реализации единицы продукции для этих изделий представлены в табл. 3.4. Определим из предложенных видов изделий выгодные для предприятия с экономической точки зрения.

Таблица 3.4

Ресурсы	Объективно обусловленные оценки ресурсов	Затраты ресурсов на одно изделие
		В	Г	Д
Труд	40/3	6	4	2
Сырье	0	2	1	3
Оборудование	20/3	3	1	2
Прибыль на одно изделие		80	70	45

Эту задачу можно решить на основании свойства 3 двойственных оценок: в оптимальный план задачи на получение максимума прибыли может быть включен лишь тот вариант, для которого прибыль, недополученная из-за отвлечения дефицитных ресурсов, т.е. величина 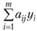, покрывается полученной прибылью с_j. Таким образом, характеристикой того или иного варианта служит разность 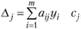, при этом если 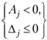, то вариант выгоден; если 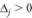, то невыгоден.

Для решения задачи воспользуемся соотношением и рассчитаем характеристики новых изделий.

Для изделия В:

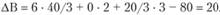
Поскольку 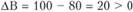, то делаем вывод, что изделие В невыгодно для включения в план, так как затраты на его изготовление не покрываются получаемой прибылью.

Аналогично для изделия Г:

∆Г = 4 - 40/3 + 20/3 - 70 = 160/3 - 20/3 - 70 = 180/3 - 70 = 60 - 70 = -10 < 0 - выгодно;

для изделия Д:

∆Д = 2 · 40/3 + 20/3 · 2 - 45 = 80/3 + 40/3 - 45 = 40 - 45 = -5 < 0 - выгодно.

В рассмотренных выше задачах детально изучены три первых свойства двойственных оценок и использование этих свойств при анализе оптимальных решений экономических задач: оценки как меры дефицитности ресурсов, оценки как меры влияния ограничений на функционал, оценки как инструмент определения эффективности отдельных вариантов.

Свойство 4 - оценки как инструмент балансирования суммарных затрат и результатов - вытекает из первой теоремы двойственности, в которой устанавливается связь между функционалами прямой и двойственной задач: max 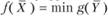. В конкретных задачах такого рода соотношения "затраты - результаты", т.е. равновесие затрат и результатов в точке оптимума, могут иметь различное экономическое содержание.

В рассматриваемых нами задачах экономический смысл равенства функционалов прямой и двойственной задач состоит в том, что максимум прибыли может быть обеспечен лишь при минимуме недополученной прибыли от использования дефицитных ресурсов.

Транспортная задача

Как показано выше, многие прикладные модели в экономике сводятся к задачам линейного программирования. Практически все задачи линейного программирования можно решить, используя ту или иную модификацию симплексного метода. Однако существуют более эффективные вычислительные процедуры решения некоторых типов задач линейного программирования, основанные на специфике ограничений этих задач. Рассмотрим так называемую транспортную задачу по критерию стоимости, которую можно сформулировать следующим образом.

В m пунктах отправления А₁, А₂, ..., А_m, которые в дальнейшем будем называть поставщиками, сосредоточено определенное количество единиц некоторого однородного продукта, которое обозначим a_i (i = 1, 2,..., m). Данный продукт потребляется в n пунктах В₁, В₂,..., В_n, которые будем называть потребителями; объем потребления обозначим b_j (j = 1,2,..., п). Известны расходы на перевозку единицы продукта из пункта А_i в пункт B_j, которые равны С_у и приведены в матрице транспортных расходов С = (с_ij).

Требуется составить такой план прикрепления потребителей к поставщикам, т.е. план перевозок, при котором весь продукт вывозится из пунктов A_j в пункты в соответствии с потребностью и общая величина транспортных издержек будет минимальной.

Обозначим количество продукта, перевозимого из пункта A_i в пункт В_j через х_ij. Совокупность всех переменных Xj для краткости обозначим X, тогда целевая функция задачи будет иметь вид

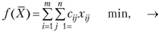(3.15)

а ограничения выглядят следующим образом:

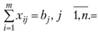(3.16)

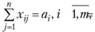(3.17)

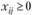
Условия (3.16) означают полное удовлетворение спроса во всех пунктах потребления; условия (3.17) определяют полный вывоз продукции от всех поставщиков.

Необходимым и достаточным условием разрешимости задачи (3.15)-(3.17) является условие баланса:

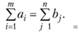(3.18)

Транспортная задача, в которой имеет место равенство (3.18), называется закрытой и может быть решена как задача линейного программирования с помощью симплексного метода. Однако благодаря особенностям переменных задачи и системы ограничений разработаны специальные, менее громоздкие методы ее решения. Наиболее применяемым методом является метод потенциалов, при котором каждой i-й строке (i-му поставщику) устанавливается потенциал u_j, который можно интерпретировать как цену продукта в пункте поставщика, а каждому столбцу j (j-му потребителю) устанавливается потенциал Vj, который можно принять условно за цену продукта в пункте потребителя. В простейшем случае цена продукта в пункте потребителя равна его цене в пункте поставщика плюс транспортные расходы на его доставку, т.е.

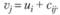(3.19)

Алгоритм метода потенциалов для закрытой транспортной задачи детально описан в ряде учебных пособий (см., например, [6]). Первым этапом этого алгоритма является составление начального распределения (начального плана перевозок); для реализации этого начального этапа имеется в свою очередь ряд методов: северо-западного угла, наименьших стоимостей, аппроксимаций Фогеля и др. Вторым этапом служат построение системы потенциалов на основе равенства (3.19) и проверка начального плана на оптимальность; в случае его неоптимальности переходят к третьему этапу, содержание которого заключается в реализации так называемых циклов перераспределения (корректировка плана прикрепления потребителей к поставщикам), после чего переходят опять ко второму этапу. Совокупность процедур третьего и второго этапов образует одну итерацию; эти итерации повторяются, пока план перевозок не окажется оптимальным по критерию (3.15).

Если баланс (3.18) не выполняется, то ограничения (3.16) или (3.17) имеют вид неравенств типа "меньше или равно"; транспортная задача в таком случае называется открытой. Для решения открытой транспортной задачи методом потенциалов ее сводят к закрытой задаче путем ввода или фиктивного потребителя, если в неравенства превращаются условия (3.17), или фиктивного поставщика - в случае превращения в неравенства ограничений (3.16) (см. ниже пример 3.5).

Рассмотрим этапы реализации метода потенциалов для закрытой транспортной задачи более подробно. Прежде всего следует отметить, что при условии баланса (3.18) ранг системы линейных уравнений (3.16), (3.17) равен т + п - 1; таким образом из общего числа m x n неизвестных базисных неизвестных будет т + п - 1. Вследствие этого при любом допустимом базисном распределении в матрице перевозок (таблице поставок), представленной в общем виде в табл. 3.5, будет занято ровно т + п - 1 клеток, которые будем называть базисными в отличие от остальных, свободных, клеток; занятые клетки будем отмечать диагональной чертой.

Таблица 3.5

Мощности поставщиков	Мощности потребителей
	b1	b2	…	bn
a1	c11 x11	c12 x12	…	c1n x 1n
a2	c21 x21	c22 x 22	…	c2n x 2n
…	…	…	…	…
an	cm1 x m2	cm2 xm2	…	cmn x mn

Этап 1. Первоначальное закрепление потребителей за поставщиками. Рассмотрим два метода получения начального распределения (начального опорного плана): метод северо-западного угла и метод наименьших стоимостей. При каждом из этих методов при заполнении некоторой клетки, кроме последней, вычеркивается или только строка матрицы перевозок, или только столбец; лишь при заполнении последней клетки вычеркиваются и строка, и столбец. Такой подход будет гарантировать, что базисных клеток будет ровно т + п - 1. Если при заполнении некоторой (не последней) клетки одновременно удовлетворяются мощности и поставщика, и потребителя, то вычеркивается, например, только строка, а в соответствующем столбце заполняется незанятая клетка так называемой нулевой поставкой, после чего вычеркивается и столбец. Для идентификации клетки обычно в скобках указываются номера ее строки и столбца.

В методе северо-западного угла всегда в первую очередь заполняется клетка (из числа невычеркнутых), стоящая в верхнем левом (северо-западном) углу матрицы перевозок. Пример составления начального распределения данным методом показан в табл. 3.6: заполняется клетка (1; 1) и вычеркивается первый столбец, заполняется клетка (1; 2) и вычеркивается первая строка; заполняется клетка (2; 2) и вычеркивается второй столбец; заполняется клетка (2; 3) и вычеркивается вторая строка; заполняется клетка (3; 3) и вычеркивается третий столбец; наконец, заполняется клетка (3; 4) и вычеркиваются последние строка и столбец. Число запятых клеток равно m + n - 1 = 3 + 4 - 1 = 6. Суммарные затраты на реализацию данного плана перевозок составят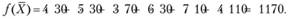

Таблица 3.6

Мощности поставщиков	Мощности потребителей
	30	100	40	110
60	4 30	5 30	2	3
100	1	3 70	6 30	2
120	6	2	7 10	4 110

Недостатком данного метода является то, что он не учитывает значения элементов с_# матрицы транспортных расходов, в результате чего полученное этим методом начальное распределение (начальный опорный план перевозок) может быть достаточно далеко от оптимального.

В различных модификациях метода наименьших стоимостей заполнение клеток матрицы перевозок проводится с учетом значений величин с_ij. Так, в модификации "двойного предпочтения" отмечают клетки с наименьшими стоимостями перевозок сначала по каждой строке, а затем по каждому столбцу. Клетки, имеющие две отметки, заполняют в первую очередь, затем заполняют клетки с одной отметкой, а данные о нераспределенном грузе записывают в неотмеченные клетки с наименьшими стоимостями. При этом из двух клеток с одинаковой стоимостью перевозок предпочтение отдается клетке, через которую осуществляется больший объем перевозок. Вычеркивание строк и столбцов при заполнении клеток проводится по описанным выше правилам. Пример начального распределения методом наименьших стоимостей дня тех же исходных данных, что и ранее, представлен в табл. 3.7.

Порядок заполнения клеток: (2; 1), (3; 2), (1; 3), (2; 4), (1; 4), (3; 4). Суммарные затраты на перевозки, представленные в табл. 3.7, составляют

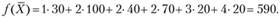
Таблица 3.7

Мощности поставщиков	Мощности потребителей
	30	100	40	110
60	4	5	2 40	3 20
100	1 30	3	6	2 70
120	6	2 100	7	4 20

Следовательно, данный план перевозок значительно ближе к оптимальному, чем план, составленный по методу северо-западного угла.

Этап 2. Проверка оптимальности полученного плана перевозок. Введем специальные показатели и, для каждой строки матрицы перевозок (каждого поставщика), где 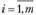, и показатели Vj для каждого столбца (каждого потребителя), где 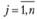. Эти показатели называются потенциалами поставщиков и потребителей, их удобно интерпретировать как цены продукта в соответствующих пунктах поставщиков и потребителей. Потенциалы подбираются таким образом, чтобы для заполненной клетки (i; j) выполнялось равенство (3.19). Совокупность уравнений вида (3.19), составленных для всех заполненных клеток (всех базисных неизвестных), образует систему т + п - 1 линейных уравнений с т + п неизвестными u_i, и v_y. Эта система всегда совместна, причем значение одного из неизвестных можно задавать произвольно (например, и_; = 0), тогда значения остальных неизвестных находятся из системы однозначно.

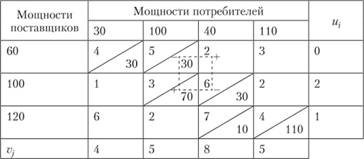
Рассмотрим процесс нахождения потенциалов для базисного начального распределения по методу северо-западного угла, представленного в табл. 3.6. Задав и, = 0 и используя формулу (3.19) для заполненных клеток (1; 1) и (1; 2), находим V = 4 и v₂ = 5. Зная v₂, по заполненной клетке (2; 2) находим и_Л = 2, а зная v₂, по заполненной клетке (2;

2) находим ?'₃ = 8. Зная у₃, по заполненной клетке (3; 3) находим щ = 1, а затем по заполненной клетке (3; 4) находим

= 5. Результаты представлены в табл. 3.8, где потенциалы

поставщиков приведены в последнем столбце, а потенциалы потребителей - в последней строке.

Смысл прямоугольного контура, проведенного пунктиром в табл. 3.8, и знаков при его вершинах пояснен далее при описании этапа 3 метода потенциалов.

Таблица 3.8

Аналогичные результаты для начального распределения по методу наименьших стоимостей, приведенного в табл. 3.7, представлены в табл. 3.9.

Таблица 3.9

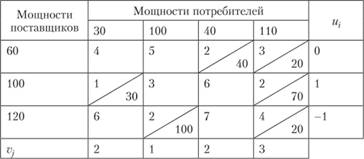
Чтобы оценить оптимальность распределения, для всех клеток (i, j) матрицы перевозок определяются их оценки, которые обозначим через ∆_ij, по формуле

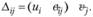(3.20)

Используя ранее принятую интерпретацию, выражение (Uj+Cjj) можно трактовать как сумму цены продукта у поставщика и стоимости перевозки; эта сумма путем вычитания сравнивается с ценой продукта у соответствующего потребителя V:. Очевидно, оценки заполненных клеток равны нулю (цена потребителя покрывает цену поставщика и стоимость перевозок). Таким образом, об оптимальности распределения можно судить но величинам оценок свободных клеток. Если оценка некоторой свободной клетки отрицательна, это можно интерпретировать так: цена, предлагаемая соответствующим потребителем, больше суммы цены поставщика и стоимости перевозки, т.е. если бы эта клетка была занята, то можно было бы получить дополнительный экономический эффект. Следовательно, условием оптимальности распределения служит условие неотрицательности оценок свободных клеток матрицы перевозок.

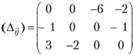
Оценки клеток по формуле (3.20) удобно представить в виде матрицы оценок. Для ранее рассматриваемого распределения, полученного методом северо-западного угла (см. табл. 3.8), матрица оценок клеток имеет вид

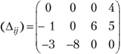(3.21)

Наличие большего числа отрицательных оценок свободных клеток свидетельствует о том, что данный план перевозок далек от оптимального (напомним, что суммарные затраты на перевозку по этому плану равны 1170).

Для распределения, полученного методом наименьших стоимостей (см. табл. 3.9), матрица оценок клеток имеет вид

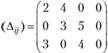
Так как все оценки неотрицательны, то не имеется возможности улучшить данный план перевозок, т.е. он оптимален (суммарные затраты на перевозку по этому плану равны 590). Кроме того, следует отметить, что в данном случае оценки всех свободных клеток строго больше нуля, т.е. любой другой план, предусматривающий занятие хотя бы одной из этих клеток, будет менее оптимален. Это говорит о том, что найденный оптимальный план является единственным. Наличие нулевых оценок свободных клеток в оптимальном плане перевозок, наоборот, свидетельствует о неединственности оптимального плана.

Этап 3. Улучшение неоптимального плана перевозок (циклы перераспределения). Чтобы улучшить неоптимальный план перевозок, выбирается клетка матрицы перевозок с отрицательной оценкой; если таких клеток несколько, то обычно (но необязательно) выбирается клетка с наибольшей по абсолютной величине отрицательной оценкой. Например, для распределения, представленного в табл. 3.8, такой клеткой может служить клетка (1; 3) (см. матрицу оценок (3.21)).

Для выбранной клетки строится замкнутая линия (контур), начальная вершина которой лежит в выбранной клетке, а все остальные вершины находятся в занятых клетках; при этом направления отдельных отрезков контура могут быть только горизонтальными и вертикальными. Вершиной контура, кроме первой, является занятая клетка, где отрезки контура образуют один прямой угол (нельзя рассматривать как вершины клетки, где горизонтальные и вертикальные отрезки контура пересекаются). Очевидно, число отрезков контура, как и его вершин, будет четным. В вершинах контура расставляются поочередно знаки "+" и "-", начиная со знака "+" в выбранной свободной клетке. Пример простого контура показан пунктиром в табл. 3.8, хотя вид контура может быть самым разнообразным (см., например, контур в табл. 3.11).

Величина перераспределяемой поставки определяется как наименьшая из величин поставок в вершинах контура со знаком "-", и на эту величину увеличиваются поставки в вершинах со знаком "+" и уменьшаются поставки в вершинах со знаком "-". Это правило гарантирует, что в вершинах контура не появится отрицательных поставок, начальная выбранная клетка окажется занятой, в то время как одна из занятых клеток при этом обязательно освободится. Если величина перераспределяемой поставки равна поставкам не в одной, а в нескольких вершинах контура со знаком "-" (это как раз имеет место в контуре перераспределения в табл. 3.8), то освобождается только одна клетка, обычно с наибольшей стоимостью перевозки, а все другие такие клетки остаются занятыми с нулевой поставкой.

Результат указанных операций для представленного в табл. 3.8 распределения поставок показан в табл. 3.10. Суммарные затраты на перевозки по этому плану составляют:

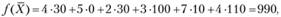
что значительно меньше предыдущей суммы затрат 1170, хотя план перевозок в табл. 3.10 еще не является оптимальным. Об этом свидетельствует наличие отрицательных значений в матрице оценок клеток этого плана (соответствующие потенциалы u_i и v_j найдены способом, изложенным при описании этапа 2):

Таблица 3.10

Мощности поставщиков	Мощности потребителей				ui
	30	100	40	110
60	4 30	5 0	2 30	3	0
100	1	3 100	6	2	2
120	6	2	7 10	4 110	-5
vi	4	5	2	-1

Транспортные задачи, в базисном плане перевозок которых имеют место занятые клетки с нулевой поставкой (или в первоначальном распределении, или в процессе итераций), называются вырожденными; пример такой задачи представлен в табл. 3.10. В случае вырожденной транспортной задачи существует опасность зацикливания, т.е. бесконечного повторения итераций (бесконечного перебора одних и тех же базисных комбинаций занятых клеток). Как правило, в практических задачах транспортного типа зацикливание не встречается, тем не менее следует знать, что существуют специальные правила, позволяющие выйти из цикла, если зацикливание все же произойдет. При отсутствии вырождения метод потенциалов конечен и приводит к оптимальному плану перевозок за конечное число шагов.

Пример 3.4. Решим методом потенциалов закрытую транспортную задачу, заданную в табл. 3.11, в которую уже внесено некоторое допустимое базисное распределение. Суммарные транспортные расходы составляют при этом плане перевозок

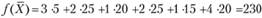
Потенциалы по формуле (3.19) находим следующим образом: задавая u_{ = 0, находим по клетке (1; 1) = 3, по клетке (1; 2) = 2, а по клетке (1; 4) = 1; затем по клетке (2; 1) находим и₂ = 1 и по клетке (2; 3) v₃ = 2; наконец, по клетке (3; 3) находим u₃ = -2.

Таблица 3.11

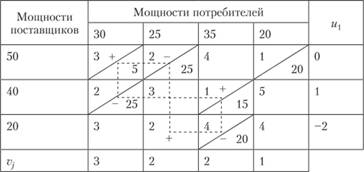
Матрица оценок клеток для этого плана рассчитывается по формуле (3.21):

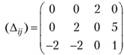
Наличие отрицательных оценок свидетельствует о том, что план неоптимален. Построим контур перераспределения, например, для клетки (3; 2) в табл. 3.11 он показан пунктиром и его вершинам присвоены соответствующие знаки.

Наименьшая поставка в вершине контура со знаком "-" равна 20, поэтому проведем перераспределение поставок, уменьшив поставки в клетках со знаком "-" на 20 и увеличив поставки в клетках со знаком "+" также на 20; при этом клетка (3; 2) заполняется, а клетка (3; 3) освобождается. Новый план представлен в табл. 3.12, соответствующие значения потенциалов показаны в последних столбце и строке.

Таблица 3.12

Мощности поставщиков	Мощности потребителей				ui
	30	25	3	20
50	3 25	2 5	4	1 20	0
40	2 5	3	1 35	5	1
20	3	2 20	4	4	0
vj	3	2	2	1

Матрица оценок клеток этого распределения не содержит отрицательных значений, следовательно, данный план перевозок является оптимальным, стоимость перевозок по этому плану равна

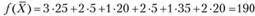
Наличие нулевой оценки незанятой клетки (3;1) говорит о том, что оптимальный план не является единственным. Можно отметить также, что, применяя для начального распределения в этой транспортной задаче модификацию двойного предпочтения метода наименьших стоимостей, мы сразу же получили бы оптимальное распределение, представленное в табл. 3.12.

Пример 3.5. Рассмотрим пример решения открытой транспортной задачи, исходные данные которой представлены в табл. 3.13.

Таблица 3.13

Мощности поставщиков	Мощности потребителей
	30	100	40	100
60	4	5	2	3
100	1	3	6	2
120	6	2	7	4

Проверим выполнение условия баланса (3.18):

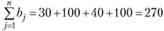
Условие баланса не выполняется, следовательно, задача действительно является открытой. Сформулируем экономико-математическую модель этой задачи.

Пусть Х_y- объемы перевозок от г-го поставщика j-му потребителю. Целевая функция задачи будет иметь вид

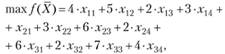
а ограничения выглядят следующим образом: по поставщикам:

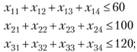
по потребителям: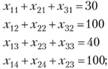

прямые ограничения: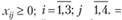

Сведем эту задачу к закрытой, введя фиктивного потребителя с мощностью 280 - 270 = 10; стоимости перевозок единицы груза в соответствующих (фиктивных) клетках принимаются равными нулю, и эти клетки при составлении начального распределения перевозок заполняются в самую последнюю очередь. Начальный план перевозок но методу наименьших стоимостей представлен в табл. 3.14.

Матрица оценок клеток этого плана в соответствии с методом потенциалов имеет вид

Таблица 3.14

Мощности поставщиков	Мощности потребителей					и,
	30	100	40	100	10
60	4	5	2 40	3 20	0	0
100	1 30	3	6	2 70	0	1
120	6	2 100	7	4 70	0 10	-1
	2	1	2	3	-1

Анализ элементов матрицы оценок клеток свидетельствует о том, что план перевозок в табл. 3.14 является оптимальным и единственным. Стоимость перевозок по этому плану составит 550, при этом мощности потребителей будут удовлетворены полностью, а у третьего поставщика останутся невывезенными 10 единиц груза.