Рассмотрим основные понятия и выводы специального раздела линейного программирования - теория двойственности. В главе 2 показано, что любую задачу линейного программирования можно записать следующим образом:
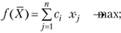 (3.1)
(3.1)
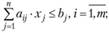 (3.2)
(3.2)
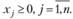 (3.3)
(3.3)
В этой главе для большей наглядности используются записи типа 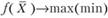 , эквивалентные записям
, эквивалентные записям 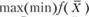 .
.
С каждой задачей линейного программирования тесно связана другая линейная задача, называемая двойственной, первоначальная задача называется исходной или прямой.
Связь исходной и двойственной задач заключается, в частности, в том, что решение одной из них может быть получено непосредственно из решения другой.
Хорошо разработанный математический аппарат линейного программирования позволяет не только получать с помощью эффективных вычислительных процедур оптимальный план, но и делать ряд экономически содержательных выводов, основанных на свойствах задачи, двойственной к исходной ЗЛП. Переменные двойственной задачи у, называют объективно обусловленными оценками или двойственными оценками. Модель двойственной задачи имеет вид
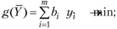 (3.4)
(3.4)
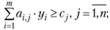 (3.5)
(3.5)
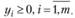 (3.6)
(3.6)
Каждая из задач двойственной пары фактически является самостоятельной задачей линейного программирования и может быть решена независимо от другой. Однако при определении симплексным методом оптимального плана одной из задач находится решение и другой задачи.
Двойственная задача, по отношению к исходной, составляется согласно следующим правилам:
1) целевая функция исходной задачи (3.1)-(3.3) формулируется на максимум, а целевая функция двойственной задачи (3.4)-(3.6) - на минимум, при этом в задаче на максимум все неравенства в функциональных ограничениях имеют вид "≤", а в задаче на минимум - вид "≥";
2) Матрица
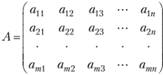
составленная из коэффициентов при неизвестных в системе ограничений (3.2) исходной задачи, и аналогичная матрица
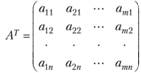
в двойственной задаче получаются друг из друга транспонированием;
3) число переменных в двойственной задаче равно числу функциональных ограничений (3.2) исходной задачи, а число ограничений в системе (3.5) двойственной задачи - числу переменных в исходной задаче;
4) коэффициентами при неизвестных в целевой функции (3.4) двойственной задачи являются свободные члены в системе (3.2) ограничений исходной задачи, а правыми частями в ограничениях (3.5) двойственной задачи - коэффициенты при неизвестных в целевой функции (3.1) исходной задачи;
5) каждому ограничению одной задачи соответствует переменная другой задачи: номер переменной совпадает с номером ограничения; при этом ограничению, записанному в виде неравенства "<", соответствует переменная, связанная условием неотрицательности. Если функциональное ограничение исходной задачи является равенством, то соответствующая переменная двойственной задачи может принимать как положительные, так и отрицательные значения.
Математические модели пары двойственных задач могут быть симметричными и несимметричными. В несимметричных двойственных задачах система ограничений исходной задачи задается в виде равенств, а двойственной - в виде неравенств, причем в последней переменные могут быть и отрицательными. В симметричных задачах система ограничений как исходной, так и двойственной задачи задается неравенствами, причем на двойственные переменные налагается условие неотрицательности. В дальнейшем мы будем рассматривать только симметричные взаимодвойственные задачи линейного программирования.
Итак, согласно теории линейного программирования каждой ЗЛП вида (3.1)-(3.3) соответствует двойственная ей ЗЛП: (3.4)-(3.6). Основные утверждения о взаимодвойственных задачах содержатся в двух следующих теоремах.
Дата: 2019-02-25, просмотров: 338.