Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Лекция 3 Оптимизационные экономико-математические модели

- Теория двойственности в анализе оптимальных решений экономических задач

- Транспортная задача

- Целочисленное программирование

- Задачи многокритериальной оптимизации

- Нелинейное и динамическое программирование; понятие об имитационном моделировании

- Модели сетевого планирования и управления

В результате изучения материала этой главы студенты должны:

знать:

o основные понятия теории двойственности линейного программирования;

o методы формулировки и решения транспортных задач;

o особенности методов целочисленного, нелинейного, динамического программирования и имитационного моделирования;

o принципы и методы использования сетевых моделей в экономике;

уметь:

o использовать при анализе оптимальных решений теоремы двойственности;

o решать закрытые и открытые транспортные задачи;

o применять методы целочисленного и многокритериального программирования при решении практических задач;

o строить сетевые модели и оптимизировать их;

владеть:

o понятийным аппаратом теории двойственности;

o практическими навыками постановки и решения транспортных задач, задач целочисленного программирования и многокритериальной оптимизации, задач сетевого планирования и управления.

Первая теорема двойственности

Для взаимодвойственных ЗЛП имеет место один из взаимоисключающих случаев.

1. В прямой и двойственной задачах имеются оптимальные решения, при этом значения целевых функций на оптимальных решениях совпадают: max f(X) = min g(Y).

2. В прямой задаче допустимое множество не пусто, а целевая функция на этом множестве не ограничена сверху. При этом у двойственной задачи будет пустое допустимое множество.

3. В двойственной задаче допустимое множество не пусто, а целевая функция на этом множестве не ограничена снизу. При этом у прямой задачи допустимое множество оказывается пустым.

4. Обе из рассматриваемых задач имеют пустые допустимые множества.

Вторая теорема двойственности (теорема о дополняющей нежесткости)

Пусть 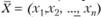- допустимое решение прямой задачи (3.1)-(3.3), а 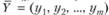- допустимое решение двойственной задачи (3.4)-(3.6). Для того чтобы они были оптимальными решениями соответствующих взаимодвойсгвенных задач (3.1)-(3.3) и (3.4)-(3.6), необходимо и достаточно, чтобы выполнялись следующие соотношения:

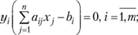(3.7)

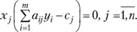(3.8)

Условия (3.7) и (3.8) позволяют, зная оптимальное решение одной из взаимодвойственных задач, найти оптимальное решение другой задачи.

Рассмотрим еще одну теорему, выводы которой будут использованы в дальнейшем.

Таблица 3.1

Исходные данные

Вид сырья	Запасы сырья	Вид продукции
		Р1	Р2	Р3	Р4
S1	35	4	2	2	3
S2	30	1	1	2	3
S3	40	3	1	2	1
Прибыль		14	10	14	11

Модель задачи по критерию "максимум прибыли":

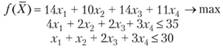
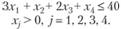
Теперь сформулируем двойственную задачу. Пусть некая организация решила закупить все ресурсы рассматриваемого предприятия. При этом необходимо установить оптимальную цену на приобретаемые ресурсы у₁, у₂, y₃ исходя из следующих объективных условий:

1) покупающая организация старается минимизировать общую стоимость ресурсов;

2) за каждый вид ресурсов надо уплатить не менее той суммы, которую хозяйство может выручить при переработке сырья в готовую продукцию.

Согласно первому условию общая стоимость сырья выразится величиной 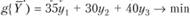. Согласно второму требованию вводятся ограничения: на единицу первого вида продукции расходуются четыре единицы первого ресурса ценой y₁, одна единица второго ресурса ценой у₂ и три единицы третьего ресурса ценой у₃. Стоимость всех ресурсов, расходуемых на производство единицы первого вида продукции, равна 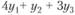и должна составлять не менее 14, т.е.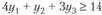

В результате аналогичных рассуждений относительно производства второго, третьего и четвертого видов продукции получаем систему неравенств:

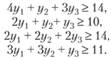
По экономическому смыслу цены неотрицательные:

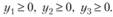
Получили симметричную пару взаимодвойственных задач. В результате решения данной задачи симплексным методом получен оптимальный план 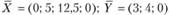. На рис. 3.1 приведен результат решения задачи с использованием надстройки Поиск решения Excel. Жирным шрифтом выделены оптимальные значения 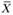и .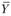

Экономический смысл первой теоремы двойственности следующий. План производства X и набор оценок ресурсов Y оказываются оптимальными тогда и только тогда, когда прибыль от реализации продукции, определенная при известных заранее ценах продукции с₁, с₂,..., с₃, равна затратам на ресурсы но "внутренним" (определяемым только из решения задачи) ценам ресурсов у₁, у_2,…,у_т. Для всех же других планов 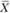и 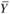обеих задач прибыль от продукции всегда меньше (или равна) стоимости затраченных ресурсов: 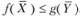, т.е. ценность всей выпущенной продукции не превосходит суммарной оценки имеющихся ресурсов. Значит, величина 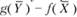характеризует производственные потери в зависимости от рассматриваемой производственной программы и выбранных оценок ресурсов.

Ячейки переменных

Ячейка Имя Окончательное значение Приведенная стоимость

Целевая функция

Коэффициент

Допустимое увеличение Допустимое уменьшение SBS1   0 -2 14

2

1Е+30 SCSI   5 0 10

4

0.666666667 SDS1   12,5 0 14

2

4 SES1   0 -10 11

10

1Е+30

Ограничения

Ячейка Имя Окончательное значение Теневая цена Ограничение Правая сторона

Допустимое увеличение

Допустимое уменьшение SFS3   35 3 35

25

5 SFS4   30 4 30

5

12.5 $Н$5   30 0 40

1Е+30

10                

Рис. 3.1. Отчет по устойчивости Microsoft Excel

Из первой теоремы двойственности следует, что при оптимальных производственной программе и векторе оценок ресурсов производственные потери равны нулю.

Экономический смысл первой теоремы двойственности можно интерпретировать и так: предприятию безразлично, производить ли продукцию по оптимальному плану 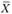и получить максимальную прибыль либо продать ресурсы по оптимальным ценам 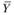и возместить от продажи равные ей минимальные затраты на ресурсы.

Из второй теоремы двойственности в данном случае следуют такие требования на оптимальную производственную программу 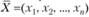и оптимальный вектор оценок :

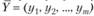если 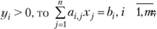(3.10)

если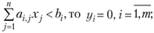

если 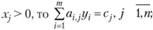(3.11)

если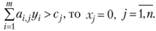

Условия (3.10) можно интерпретировать так: если оценка у_i, единицы ресурса г-го вида положительна, то при оптимальной производственной программе этот ресурс используется полностью; если же ресурс используется не полностью, то его оценка равна нулю.

Из условия (3.11) следует, что если j-й вид продукции вошел в оптимальный план, то он в оптимальных оценках не убыточен; если же j-й вид продукции убыточен, то он не войдет в план, не будет выпускаться.

Кроме нахождения оптимального решения должно быть обеспечено получение дополнительной информации о возможных изменениях решения при изменении параметров системы. Эту часть исследования обычно называют анализом модели на чувствительность. Он необходим, например, в тех случаях, когда некоторые характеристики исследуемой системы не поддаются точной оценке.

Экономико-математический анализ решений осуществляется в двух основных направлениях: в виде вариантных расчетов по моделям с сопоставлением различных вариантов плана и в виде анализа каждого из полученных решений с помощью двойственных оценок. Вариантные расчеты могут осуществляться при неизменной структуре самой модели (постоянном составе неизвестных, способов производства, ограничений задачи и одинаковом критерии оптимизации), но с изменением численной величины конкретных показателей модели. Вариантные расчеты могут проводиться также при варьировании элементов самой модели: изменении критерия оптимизации, добавлении новых ограничений на ресурсы или на способы производства их использования, расширения множества вариантов и т.д.

Одно из эффективных средств экономико-математического анализа - использование объективно обусловленных оценок оптимального плана. Такого рода анализ базируется на свойствах двойственных оценок. Выше мы установили общие математические свойства двойственных оценок для задач на оптимум любой экономической природы. Однако экономическая интерпретация этих оценок может быть совершенно различной для разных задач.

Перейдем к рассмотрению конкретных экономических свойств оценок y_i, оптимального плана. Сначала перечислим эти свойства, а затем проиллюстрируем их конкретными примерами.

Свойство 1. Оценки как мера дефицитности ресурсов и продукции.

Свойство 2. Оценки как мера влияния ограничений на функционал.

Свойство 3. Оценки как инструмент определения эффективности отдельных вариантов.

Свойство 4. Оценки как инструмент балансирования суммарных затрат и результатов.

Пример 3.2 (задача о планировании выпуска тканей). Пусть некоторая фабрика выпускает три вида тканей, причем суточное плановое задание составляет не менее 90 м тканей первого вида, 70 м - второго и 60 м - третьего. Суточные ресурсы следующие: 780 единиц производственного оборудования, 850 единиц сырья и 790 единиц электроэнергии, расход которых на один метр ткани представлен в табл. 3.2.

Таблица 3.2

Нормы расхода ресурсов

Ресурсы	Ткани
	I	II	III
Оборудование	2	3	4
Сырье	I	4	э
Электроэнергия	3	4	2

Цена за один метр ткани вида I равна 80 денежным единицам, II - 70 денежным единицам, III - 60 денежным единицам.

Необходимо определить, сколько метров ткани каждого вида следует выпустить, чтобы общая стоимость выпускаемой продукции была максимальной.

Решение. Составим модель задачи. Введем следующие обозначения. Неизвестными в задаче являются объемы выпуска ткани каждого вида:

x₁ - количество метров ткани вида I;

х₂ - количество метров ткани вида II;

х₃ - количество метров ткани вида III.

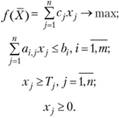
С учетом имеющихся данных модель примет вид:

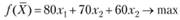
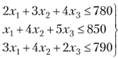Ограничение по ресурсам

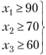Плановое задание

В результате решения задачи симплексным методом получен следующий оптимальный план: максимум общей стоимости продукции 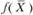= 19 075 ден. ед. достигается при

x₁ = 112,5 м - оптимальный объем выпуска ткани вида I;

x₂ = 70 м - оптимальный объем выпуска ткани вида II;

x₃ = 86,25 м - оптимальный объем выпуска ткани вида III.

Решение двойственной задачи получим с использованием теорем двойственности. Введем обозначения:

y₁ - двойственная оценка ресурса "оборудование";

y₂ - двойственная оценка ресурса "сырье";

y₃ - двойственная оценка ресурса "электроэнергия";

y₄ - двойственная оценка ткани вида I;

y₅ - двойственная оценка ткани вида II;

y₆ - двойственная оценка ткани вида III.

Модель двойственной задачи имеет вид:

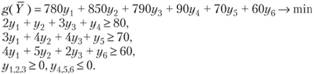
Из соотношений второй теоремы двойственности вытекают следующие условия:

для каждого ресурса:

если ;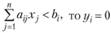

если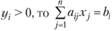

для задания по выпуску продукции:

если 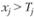, то ;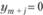

если 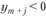, то 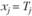. (3.12)

Для нашего примера в этих соотношениях т = 3 (количество типов ресурсов).

Подставим значения x₁ = 112,5, x₂ = 70 и x₃ = 86,25 в ограничения прямой задачи:

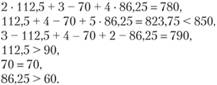
Суточные ресурсы по оборудованию и электроэнергии использованы полностью. Сырье используется не полностью, имеется остаток в размере 850 - 823,75 = 26,25 (кг). План выпуска по тканям вида I и III перевыполнен.

Из второй теоремы двойственности вытекает, что y₂, y₄ и y₆ равны нулю. Остается найти значения y₁, y₃ и y₅. Так как x₁, x₂ и x₃ - больше нуля, то все три ограничения двойственной задачи выполняются как равенства:

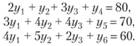
Учитывая, что 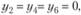имеем:

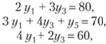
откуда .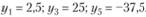

Подставив значения неизвестных в целевую функцию двойственной задачи, проверим, выполняется ли условие 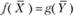для оптимального плана:

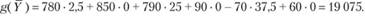
Условие первой теоремы двойственности выполняется, следовательно, рассмотренный план выпуска тканей и соответствующая ему система оценок ресурсов и продукции оптимальны.

Экономическое истолкование оценок есть интерпретация их общих экономико-математических свойств применительно к конкретному содержанию задачи. По условию (3.10) не использованный полностью в оптимальном плане ресурс получает нулевую оценку. Нулевая оценка ресурса свидетельствует о его недефицитности. Ресурс недефицитен не из-за его неограниченных запасов (они ограничены величиной b_i), а из-за невозможности его полного использования в оптимальном плане. Так как суммарный расход недефицитного ресурса меньше его общего количества, то план производства им не лимитируется. Данный ресурс не препятствует и дальше максимизировать целевую функцию .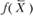

Ограничивают целевую функцию дефицитные ресурсы, в данном примере - оборудование и электроэнергия. Они полностью использованы в оптимальном плане. По условию (3.10) оценка таких ресурсов положительна (y₁ = 2,5; y₃ = 25). Рассмотрим теперь понятие дефицитности продукции. По условию (3.12) нулевую оценку (y₄ = 0, y₆ = 0) получает продукция, задания по выпуску которой в оптимальном плане перевыполняются. Очевидно, перевыполнение плана целесообразно по выгодной продукции (ткани I и III видов), т.е. такой, производство которой способствует достижению максимума критерия оптимальности. Размеры производства такой выгодной продукции определяются не величиной задания на выпуск (T_j) (в оптимальном плане они перекрыты), а ограниченностью дефицитных ресурсов. Эту продукцию выпускают как можно больше, пока хватит ресурсов. Выпуск выгодной продукции лимитируется не только фактом ограниченности дефицитных ресурсов, но и тем, что часть дефицитных ресурсов требуется выделить на обеспечение выпуска невыгодной продукции в соответствии с плановыми заданиями. По условию (3.12) отрицательную оценку (y₅ = -37,5) получает продукция, задания, по выпуску которой, не перевыполняются. Так как по условию задачи (X_j > T_j) плановые задания должны быть обязательно выполнены, то продукция делится на выгодную (виды 1 и III ткани) и невыгодную (вид II ткани).

Если в ограничение двойственной задачи, относящееся к виду II ткани,

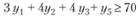
подставить полученные значения двойственных оценок, то получаем

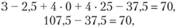
т.е. стоимость ресурсов, затраченных на один метр ткани вида II, составляет 107,5 денежной единицы, и это на 37,5 денежной единицы больше цены одного метра ткани этого вида. Таким образом, вид II ткани убыточен для фабрики: на каждом выпущенном метре ткани этого вида фабрика теряет 37,5 денежной единицы.

В соответствии с критерием оптимальности плана, в зависимости от того перевыполняется план выпуска или нет, выпуск ткани вида II поглощает часть дефицитных ресурсов, чем сдерживает рост выпуска выгодной продукции, а тем самым и рост целевой функции.

Оценка ресурса показывает, насколько изменится критерий оптимальности при изменении количества данного ресурса на единицу. Для недефицитного ресурса оценка равна нулю, поэтому изменение его величины не повлияет на критерий оптимальности. Дефицитность ресурса измеряется вкладом единицы ресурса в изменение целевой функции.

Влияние ограничений по выпуску продукции на критерий оптимальности противоположно влиянию ограничений по ресурсам. Если продукция невыгодна (вид II ткани, y₅ = -37,5), то увеличение плановых заданий по ее выпуску ведет к уменьшению выпуска выгодной продукции и ухудшает план. Наоборот, уменьшение плановых заданий по невыгодной продукции позволяет снизить ее выпуск, перебросить сэкономленные ресурсы на дополнительный сверхплановый выпуск выгодных видов продукции, что увеличивает значение целевой функции. Изменение плановых заданий по выгодной продукции не изменяет значения целевой функции.

Перейдем к анализу модели на чувствительность.

Пример 3.3. На основании информации, приведенной в табл. 3.3, составить план производства, максимизирующий объем прибыли.

Таблица 3.3

Ресурсы	Затраты ресурсов на единицу продукции		Наличие ресурсов
	А	А
Труд	2	4	2000
Сырье	4	1	1400
Оборудование	2	1	800
Прибыль на единицу продукции	40	60

Решение. Экономико-математическая модель задачи будет иметь вид:

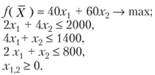
В результате решения задачи симплексным методом был получен следующий оптимальный план:

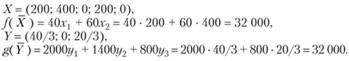
Соответствующий отчет об устойчивости решения представлен на рис. 3.2.

Ячейки переменных
Ячейка	Имя	Окончательное значение	Приведенная стоимость	Целевая функция Коэффициент		Допустимое увеличение	Допустимое уменьшение
$A$2		200	0	40	80		10
$B$2		400	0	60	20		40
Ограничения
Ячейка	Имя	Окончательное значение	Теневая цена	Ограничение Правая сторона	Допустимое увеличение		Допустимое уменьшение
$С$4		2000	13.3333333337	2000	1200		600
$С$5		1200	0	1400	1E+30		200
$С$6		800	6.6666666667	800	85.71428571		300

Рис. 3.2. Отчет об устойчивости

После того как оптимальное решение получено, выявляется его чувствительность к определенным изменениям исходной модели. В нашей задаче, например, может представить интерес то, как повлияет на оптимальное решение изменение запасов сырья и изменение прибыли от единицы продукции. В связи с этим логично выяснить.

1. Увеличение объемов какого вида ресурсов наиболее выгодно?

2. Насколько можно увеличить запас сырья для улучшения полученного оптимального значения целевой функции?

3. Каков диапазон изменения того или иного коэффициента целевой функции, при котором не происходит изменения оптимального решения?

4. Целесообразность включения в план новых изделий.

Постараемся последовательно ответить на все поставленные вопросы.

1. Ценность ресурсов. В примере 3.3 объективно обусловленные оценки ресурса "труд" равны 40/3 (y₁ = 40/3), "сырье" - 0 (y₂ = 0), "оборудование" - 20/3 (y₃ = 20/3).

Дефицитный ресурс, полностью используемый в оптимальном плане ( 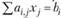), имеет положительную оценку (y_i > 0); недефицитный, не полностью используемый ресурс (для которого 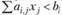), имеет нулевую оценку (y_i = 0). В примере "сырье" не является дефицитным ресурсом:

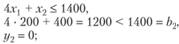
а "труд" и "оборудование" - дефицитные ресурсы:

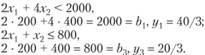
Чем выше величина оценки y_i, тем острее дефицитность i-го ресурса. В примере "труд" более дефицитен, чем "оборудование": 40/3 > 20/3. Наиболее выгодно увеличение объемов ресурса труда.

Заметим, что ценность различных видов сырья нельзя отождествлять с действительными ценами, по которым осуществляется его закупка. В данном случае речь идет о некоторой мере, имеющей экономическую природу, которая характеризует ценность сырья только относительно полученного оптимального решения.

2. Чувствительность решения к изменению запасов сырья. Предположим, что запас сырья ресурса "труд" изменился на 12 единиц, т.е. теперь он составляет 2000 + 12 = 2012 единиц.

Из теоремы об оценках 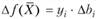известно, что колебание величины b_j приводит к увеличению или уменьшению 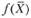. Оно определяется величиной y_i, в случае, когда при изменении величин b_j значения переменных y_i, в оптимальном плане соответствующей двойственной задачи, остаются неизменными. Поэтому необходимо найти такие интервалы изменения каждого из свободных членов системы ограничений исходной ЗЛП, в которых оптимальный план двойственной задачи не менялся бы.

Для двойственных оценок оптимального плана весьма существенное значение имеет их предельный характер.

Точной мерой влияния ограничений на функционал оценки являются лишь при малом приращении ограничения.

Известно, что оценки не меняют своей величины, если не меняется набор векторов, входящих в базис оптимального плана, тогда как интенсивность этих векторов (значения неизвестных) в плане могут меняться.

Рассмотрим модель исходной задачи (3.1)-(3.3) в матричной форме:

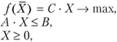
где X = (x₁, x₂,..., x_n) - вектор неизвестных;

С = (с₁, с₂,..., с_n) - вектор коэффициентов при неизвестных в целевой функции;

В = (b₁, b₂, ..., b_m) - вектор свободных членов ограничений исходной задачи;

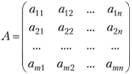- матрица коэффициентов в системе ограничений.

Приведем задачу к канонической форме, введем т дополнительных переменных. Задача примет вид:

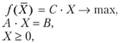
где вектор неизвестных переменных X будет теперь иметь размерность п + т. Размерность матрицы А также изменится и будет равна т · (п + т).

Пусть известен оптимальный план. Разобьем вектор X на два подвектора: 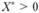и 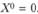. В первый включены неизвестные, вошедшие в базис оптимального решения (т.е. ненулевые в оптимальном плане). Соответственно матрицу А разобьем на две подматрицы: А* (размерность т x т) и A⁰ (размерность т x n). Первую из них сформируют т.е. столбцы матрицы А, которые соответствуют ненулевым неизвестным в оптимальном плане. Тогда 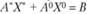. Так как 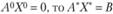. Умножив обе части последнего равенства на матрицу, обратную матрице А, получим 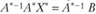. Так как 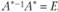, где Е - единичная матрица, то 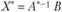. Обозначим 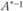через D, тогда .

Матрица D характеризует влияние ресурсов на величину выпуска продукции X. Изменим размер выделяемых ресурсов, т.е. дадим приращение 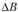вектору В. Тогда

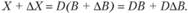
С учетом X = DB можно записать:

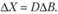
Это соотношение определяет величину структурных сдвигов в выпуске продукции при изменении ограничений исходной задачи. Из соотношений второй теоремы двойственности видно, что двойственные оценки (переменные двойственные задачи) тесным образом связаны с оптимальным планом простой задачи. Всякое изменение исходных данных прямой задачи может оказать влияние как на ее оптимальный план ( 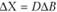), так и на систему оптимальных двойственных оценок. Поэтому, чтобы проводить экономический анализ с использованием двойственных оценок, нужно знать их интервал устойчивости.

Второе свойство двойственных оценок означает, что изменение значений величины b_i приводит к увеличению или уменьшению 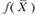. Это изменение, как выше уже отмечено, определяется величиной y_i; и может быть определено лишь тогда, когда при изменении величин b_i значения переменных y_i; в оптимальном плане соответствующей двойственной задачи остаются неизменными. Поэтому необходимо определить такие интервалы изменения каждого из свободных членов системы линейных уравнений АХ = В, в которых оптимальный план двойственной задачи не меняется. Это имеет место тогда, когда среди компонент вектора X = DB нет отрицательных.

Исходя из этого, получаем следующие оценки нижних и верхних пределов устойчивости двойственных оценок при изменении каждого ограничения в отдельности. Пределы уменьшения (нижняя граница) определяются по тем х_k(k = 1, ..., т), для которых соответствующие d_kj> 0:

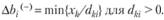(3.13)

Пределы увеличения (верхняя граница) определяются по тем х_k, для которых d_kj< 0:

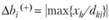для 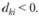(3.14)

Ослабление какого-либо i-го ограничения приводит к тому, что с определенного момента оказывается возможным изменить структуру (набор векторов) в базисе плана, что ведет к скачкообразному уменьшению величины оценки. Так продолжается до тех пор, пока i-й ресурс вообще перестанет быть дефицитным и его оценка обратится в нуль.

Определим интервалы устойчивости двойственных оценок в примере 3.3. Матрица А имеет вид

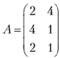
После приведения задачи к канонической форме матрица А примет следующий вид:

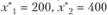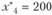С ненулевыми значениями в оптимальный план вошли и , следовательно, матрица А * будет составлена из первого, второго и четвертого столбцов матрицы А:

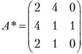
Для вычисления интервалов устойчивости необходимо найти матрицу 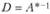(правила вычисления обратной матрицы приведены в главе 2.

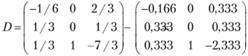
При вычислении интервалов устойчивости по формулам (3.13) и (3.14) примем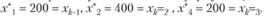

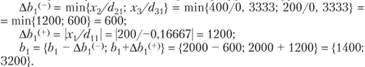
Интервалы устойчивости первого ресурса - "труд":

При изменении запасов ресурса "труд" в пределах от 1400 до 3200 единиц двойственная оценка его не изменится.

Интервалы устойчивости второго ресурса - "сырье":

этот ресурс в оптимальном плане используется не полностью и поэтому не имеет верхней границы интервалов устойчивости:

нижняя граница определяется следующим образом:

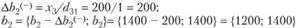
Интервалы устойчивости третьего ресурса - "оборудование":

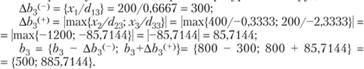
В нашем примере определим величину изменения объема прибыли от реализации продукции при увеличении ресурса "труд" на 12 единиц. Эти изменения находятся в интервалах устойчивости двойственных оценок, поэтому можно воспользоваться теоремой об оценках:

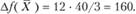
Объем прибыли увеличится на 160 единиц.

Такой же ответ мы получили бы, если бы решили симплексным методом задачу с новыми ограничениями по ресурсу "труд". Новый оптимальный план:

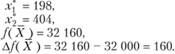
Структурных сдвигов в программе не произошло, но значения переменных в плане изменились: продукции вида Л может быть выпущено на 2 единицы меньше, а продукции вида Б - на 4 больше. Значение целевой функции при новых ограничениях увеличится на 160 единиц.

3. Чувствительность решения к изменению коэффициентов целевой функции. Так как любые изменения коэффициентов целевой функции оказывают влияние на оптимальность полученного ранее решения, то наша цель - найти такие диапазоны изменения коэффициентов в целевой функции (рассматривая каждый из коэффициентов отдельно), при которых оптимальные значения переменных остаются неизменными. Допустимые диапазоны изменения коэффициентов в целевой функции определятся из соотношений:

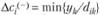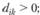
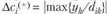для

для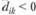

Используя эти соотношения в рассматриваемой задаче, получим для первого коэффициента целевой функции:

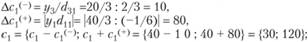
для второго коэффициента:

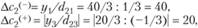
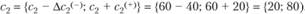
Таким образом, найденный оптимальный план выпуска продукции не будет меняться при изменении прибыли на единицу продукции А в диапазоне от 30 до 120 и прибыли на единицу второй продукции Б в диапазоне от 20 до 80.

4. Целесообразность включения в план новых изделий. Пусть в рассматриваемой нами задаче предприятию были предложены на выбор три новых изделия, за счет которых можно было бы расширить номенклатуру выпускаемой продукции при тех же запасах ресурсов. Нормы затрат ресурсов и прибыль от реализации единицы продукции для этих изделий представлены в табл. 3.4. Определим из предложенных видов изделий выгодные для предприятия с экономической точки зрения.

Таблица 3.4

Ресурсы	Объективно обусловленные оценки ресурсов	Затраты ресурсов на одно изделие
		В	Г	Д
Труд	40/3	6	4	2
Сырье	0	2	1	3
Оборудование	20/3	3	1	2
Прибыль на одно изделие		80	70	45

Эту задачу можно решить на основании свойства 3 двойственных оценок: в оптимальный план задачи на получение максимума прибыли может быть включен лишь тот вариант, для которого прибыль, недополученная из-за отвлечения дефицитных ресурсов, т.е. величина 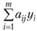, покрывается полученной прибылью с_j. Таким образом, характеристикой того или иного варианта служит разность 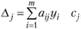, при этом если 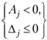, то вариант выгоден; если 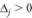, то невыгоден.

Для решения задачи воспользуемся соотношением и рассчитаем характеристики новых изделий.

Для изделия В:

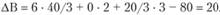
Поскольку 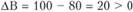, то делаем вывод, что изделие В невыгодно для включения в план, так как затраты на его изготовление не покрываются получаемой прибылью.

Аналогично для изделия Г:

∆Г = 4 - 40/3 + 20/3 - 70 = 160/3 - 20/3 - 70 = 180/3 - 70 = 60 - 70 = -10 < 0 - выгодно;

для изделия Д:

∆Д = 2 · 40/3 + 20/3 · 2 - 45 = 80/3 + 40/3 - 45 = 40 - 45 = -5 < 0 - выгодно.

В рассмотренных выше задачах детально изучены три первых свойства двойственных оценок и использование этих свойств при анализе оптимальных решений экономических задач: оценки как меры дефицитности ресурсов, оценки как меры влияния ограничений на функционал, оценки как инструмент определения эффективности отдельных вариантов.

Свойство 4 - оценки как инструмент балансирования суммарных затрат и результатов - вытекает из первой теоремы двойственности, в которой устанавливается связь между функционалами прямой и двойственной задач: max 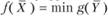. В конкретных задачах такого рода соотношения "затраты - результаты", т.е. равновесие затрат и результатов в точке оптимума, могут иметь различное экономическое содержание.

В рассматриваемых нами задачах экономический смысл равенства функционалов прямой и двойственной задач состоит в том, что максимум прибыли может быть обеспечен лишь при минимуме недополученной прибыли от использования дефицитных ресурсов.

Транспортная задача

Как показано выше, многие прикладные модели в экономике сводятся к задачам линейного программирования. Практически все задачи линейного программирования можно решить, используя ту или иную модификацию симплексного метода. Однако существуют более эффективные вычислительные процедуры решения некоторых типов задач линейного программирования, основанные на специфике ограничений этих задач. Рассмотрим так называемую транспортную задачу по критерию стоимости, которую можно сформулировать следующим образом.

В m пунктах отправления А₁, А₂, ..., А_m, которые в дальнейшем будем называть поставщиками, сосредоточено определенное количество единиц некоторого однородного продукта, которое обозначим a_i (i = 1, 2,..., m). Данный продукт потребляется в n пунктах В₁, В₂,..., В_n, которые будем называть потребителями; объем потребления обозначим b_j (j = 1,2,..., п). Известны расходы на перевозку единицы продукта из пункта А_i в пункт B_j, которые равны С_у и приведены в матрице транспортных расходов С = (с_ij).

Требуется составить такой план прикрепления потребителей к поставщикам, т.е. план перевозок, при котором весь продукт вывозится из пунктов A_j в пункты в соответствии с потребностью и общая величина транспортных издержек будет минимальной.

Обозначим количество продукта, перевозимого из пункта A_i в пункт В_j через х_ij. Совокупность всех переменных Xj для краткости обозначим X, тогда целевая функция задачи будет иметь вид

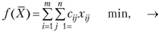(3.15)

а ограничения выглядят следующим образом:

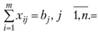(3.16)

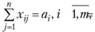(3.17)

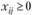
Условия (3.16) означают полное удовлетворение спроса во всех пунктах потребления; условия (3.17) определяют полный вывоз продукции от всех поставщиков.

Необходимым и достаточным условием разрешимости задачи (3.15)-(3.17) является условие баланса:

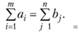(3.18)

Транспортная задача, в которой имеет место равенство (3.18), называется закрытой и может быть решена как задача линейного программирования с помощью симплексного метода. Однако благодаря особенностям переменных задачи и системы ограничений разработаны специальные, менее громоздкие методы ее решения. Наиболее применяемым методом является метод потенциалов, при котором каждой i-й строке (i-му поставщику) устанавливается потенциал u_j, который можно интерпретировать как цену продукта в пункте поставщика, а каждому столбцу j (j-му потребителю) устанавливается потенциал Vj, который можно принять условно за цену продукта в пункте потребителя. В простейшем случае цена продукта в пункте потребителя равна его цене в пункте поставщика плюс транспортные расходы на его доставку, т.е.

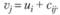(3.19)

Алгоритм метода потенциалов для закрытой транспортной задачи детально описан в ряде учебных пособий (см., например, [6]). Первым этапом этого алгоритма является составление начального распределения (начального плана перевозок); для реализации этого начального этапа имеется в свою очередь ряд методов: северо-западного угла, наименьших стоимостей, аппроксимаций Фогеля и др. Вторым этапом служат построение системы потенциалов на основе равенства (3.19) и проверка начального плана на оптимальность; в случае его неоптимальности переходят к третьему этапу, содержание которого заключается в реализации так называемых циклов перераспределения (корректировка плана прикрепления потребителей к поставщикам), после чего переходят опять ко второму этапу. Совокупность процедур третьего и второго этапов образует одну итерацию; эти итерации повторяются, пока план перевозок не окажется оптимальным по критерию (3.15).

Если баланс (3.18) не выполняется, то ограничения (3.16) или (3.17) имеют вид неравенств типа "меньше или равно"; транспортная задача в таком случае называется открытой. Для решения открытой транспортной задачи методом потенциалов ее сводят к закрытой задаче путем ввода или фиктивного потребителя, если в неравенства превращаются условия (3.17), или фиктивного поставщика - в случае превращения в неравенства ограничений (3.16) (см. ниже пример 3.5).

Рассмотрим этапы реализации метода потенциалов для закрытой транспортной задачи более подробно. Прежде всего следует отметить, что при условии баланса (3.18) ранг системы линейных уравнений (3.16), (3.17) равен т + п - 1; таким образом из общего числа m x n неизвестных базисных неизвестных будет т + п - 1. Вследствие этого при любом допустимом базисном распределении в матрице перевозок (таблице поставок), представленной в общем виде в табл. 3.5, будет занято ровно т + п - 1 клеток, которые будем называть базисными в отличие от остальных, свободных, клеток; занятые клетки будем отмечать диагональной чертой.

Таблица 3.5

Мощности поставщиков	Мощности потребителей
	b1	b2	…	bn
a1	c11 x11	c12 x12	…	c1n x 1n
a2	c21 x21	c22 x 22	…	c2n x 2n
…	…	…	…	…
an	cm1 x m2	cm2 xm2	…	cmn x mn

Этап 1. Первоначальное закрепление потребителей за поставщиками. Рассмотрим два метода получения начального распределения (начального опорного плана): метод северо-западного угла и метод наименьших стоимостей. При каждом из этих методов при заполнении некоторой клетки, кроме последней, вычеркивается или только строка матрицы перевозок, или только столбец; лишь при заполнении последней клетки вычеркиваются и строка, и столбец. Такой подход будет гарантировать, что базисных клеток будет ровно т + п - 1. Если при заполнении некоторой (не последней) клетки одновременно удовлетворяются мощности и поставщика, и потребителя, то вычеркивается, например, только строка, а в соответствующем столбце заполняется незанятая клетка так называемой нулевой поставкой, после чего вычеркивается и столбец. Для идентификации клетки обычно в скобках указываются номера ее строки и столбца.

В методе северо-западного угла всегда в первую очередь заполняется клетка (из числа невычеркнутых), стоящая в верхнем левом (северо-западном) углу матрицы перевозок. Пример составления начального распределения данным методом показан в табл. 3.6: заполняется клетка (1; 1) и вычеркивается первый столбец, заполняется клетка (1; 2) и вычеркивается первая строка; заполняется клетка (2; 2) и вычеркивается второй столбец; заполняется клетка (2; 3) и вычеркивается вторая строка; заполняется клетка (3; 3) и вычеркивается третий столбец; наконец, заполняется клетка (3; 4) и вычеркиваются последние строка и столбец. Число запятых клеток равно m + n - 1 = 3 + 4 - 1 = 6. Суммарные затраты на реализацию данного плана перевозок составят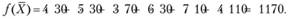

Таблица 3.6

Мощности поставщиков	Мощности потребителей
	30	100	40	110
60	4 30	5 30	2	3
100	1	3 70	6 30	2
120	6	2	7 10	4 110

Недостатком данного метода является то, что он не учитывает значения элементов с_# матрицы транспортных расходов, в результате чего полученное этим методом начальное распределение (начальный опорный план перевозок) может быть достаточно далеко от оптимального.

В различных модификациях метода наименьших стоимостей заполнение клеток матрицы перевозок проводится с учетом значений величин с_ij. Так, в модификации "двойного предпочтения" отмечают клетки с наименьшими стоимостями перевозок сначала по каждой строке, а затем по каждому столбцу. Клетки, имеющие две отметки, заполняют в первую очередь, затем заполняют клетки с одной отметкой, а данные о нераспределенном грузе записывают в неотмеченные клетки с наименьшими стоимостями. При этом из двух клеток с одинаковой стоимостью перевозок предпочтение отдается клетке, через которую осуществляется больший объем перевозок. Вычеркивание строк и столбцов при заполнении клеток проводится по описанным выше правилам. Пример начального распределения методом наименьших стоимостей дня тех же исходных данных, что и ранее, представлен в табл. 3.7.

Порядок заполнения клеток: (2; 1), (3; 2), (1; 3), (2; 4), (1; 4), (3; 4). Суммарные затраты на перевозки, представленные в табл. 3.7, составляют

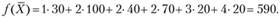
Таблица 3.7

Мощности поставщиков	Мощности потребителей
	30	100	40	110
60	4	5	2 40	3 20
100	1 30	3	6	2 70
120	6	2 100	7	4 20

Следовательно, данный план перевозок значительно ближе к оптимальному, чем план, составленный по методу северо-западного угла.

Этап 2. Проверка оптимальности полученного плана перевозок. Введем специальные показатели и, для каждой строки матрицы перевозок (каждого поставщика), где 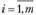, и показатели Vj для каждого столбца (каждого потребителя), где 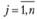. Эти показатели называются потенциалами поставщиков и потребителей, их удобно интерпретировать как цены продукта в соответствующих пунктах поставщиков и потребителей. Потенциалы подбираются таким образом, чтобы для заполненной клетки (i; j) выполнялось равенство (3.19). Совокупность уравнений вида (3.19), составленных для всех заполненных клеток (всех базисных неизвестных), образует систему т + п - 1 линейных уравнений с т + п неизвестными u_i, и v_y. Эта система всегда совместна, причем значение одного из неизвестных можно задавать произвольно (например, и_; = 0), тогда значения остальных неизвестных находятся из системы однозначно.

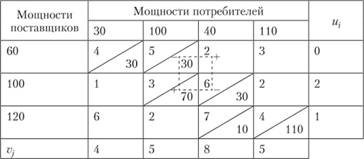
Рассмотрим процесс нахождения потенциалов для базисного начального распределения по методу северо-западного угла, представленного в табл. 3.6. Задав и, = 0 и используя формулу (3.19) для заполненных клеток (1; 1) и (1; 2), находим V = 4 и v₂ = 5. Зная v₂, по заполненной клетке (2; 2) находим и_Л = 2, а зная v₂, по заполненной клетке (2;

2) находим ?'₃ = 8. Зная у₃, по заполненной клетке (3; 3) находим щ = 1, а затем по заполненной клетке (3; 4) находим

= 5. Результаты представлены в табл. 3.8, где потенциалы

поставщиков приведены в последнем столбце, а потенциалы потребителей - в последней строке.

Смысл прямоугольного контура, проведенного пунктиром в табл. 3.8, и знаков при его вершинах пояснен далее при описании этапа 3 метода потенциалов.

Таблица 3.8

Аналогичные результаты для начального распределения по методу наименьших стоимостей, приведенного в табл. 3.7, представлены в табл. 3.9.

Таблица 3.9

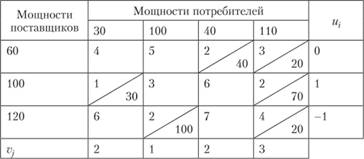
Чтобы оценить оптимальность распределения, для всех клеток (i, j) матрицы перевозок определяются их оценки, которые обозначим через ∆_ij, по формуле

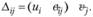(3.20)

Используя ранее принятую интерпретацию, выражение (Uj+Cjj) можно трактовать как сумму цены продукта у поставщика и стоимости перевозки; эта сумма путем вычитания сравнивается с ценой продукта у соответствующего потребителя V:. Очевидно, оценки заполненных клеток равны нулю (цена потребителя покрывает цену поставщика и стоимость перевозок). Таким образом, об оптимальности распределения можно судить но величинам оценок свободных клеток. Если оценка некоторой свободной клетки отрицательна, это можно интерпретировать так: цена, предлагаемая соответствующим потребителем, больше суммы цены поставщика и стоимости перевозки, т.е. если бы эта клетка была занята, то можно было бы получить дополнительный экономический эффект. Следовательно, условием оптимальности распределения служит условие неотрицательности оценок свободных клеток матрицы перевозок.

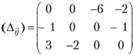
Оценки клеток по формуле (3.20) удобно представить в виде матрицы оценок. Для ранее рассматриваемого распределения, полученного методом северо-западного угла (см. табл. 3.8), матрица оценок клеток имеет вид

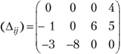(3.21)

Наличие большего числа отрицательных оценок свободных клеток свидетельствует о том, что данный план перевозок далек от оптимального (напомним, что суммарные затраты на перевозку по этому плану равны 1170).

Для распределения, полученного методом наименьших стоимостей (см. табл. 3.9), матрица оценок клеток имеет вид

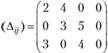
Так как все оценки неотрицательны, то не имеется возможности улучшить данный план перевозок, т.е. он оптимален (суммарные затраты на перевозку по этому плану равны 590). Кроме того, следует отметить, что в данном случае оценки всех свободных клеток строго больше нуля, т.е. любой другой план, предусматривающий занятие хотя бы одной из этих клеток, будет менее оптимален. Это говорит о том, что найденный оптимальный план является единственным. Наличие нулевых оценок свободных клеток в оптимальном плане перевозок, наоборот, свидетельствует о неединственности оптимального плана.

Этап 3. Улучшение неоптимального плана перевозок (циклы перераспределения). Чтобы улучшить неоптимальный план перевозок, выбирается клетка матрицы перевозок с отрицательной оценкой; если таких клеток несколько, то обычно (но необязательно) выбирается клетка с наибольшей по абсолютной величине отрицательной оценкой. Например, для распределения, представленного в табл. 3.8, такой клеткой может служить клетка (1; 3) (см. матрицу оценок (3.21)).

Для выбранной клетки строится замкнутая линия (контур), начальная вершина которой лежит в выбранной клетке, а все остальные вершины находятся в занятых клетках; при этом направления отдельных отрезков контура могут быть только горизонтальными и вертикальными. Вершиной контура, кроме первой, является занятая клетка, где отрезки контура образуют один прямой угол (нельзя рассматривать как вершины клетки, где горизонтальные и вертикальные отрезки контура пересекаются). Очевидно, число отрезков контура, как и его вершин, будет четным. В вершинах контура расставляются поочередно знаки "+" и "-", начиная со знака "+" в выбранной свободной клетке. Пример простого контура показан пунктиром в табл. 3.8, хотя вид контура может быть самым разнообразным (см., например, контур в табл. 3.11).

Величина перераспределяемой поставки определяется как наименьшая из величин поставок в вершинах контура со знаком "-", и на эту величину увеличиваются поставки в вершинах со знаком "+" и уменьшаются поставки в вершинах со знаком "-". Это правило гарантирует, что в вершинах контура не появится отрицательных поставок, начальная выбранная клетка окажется занятой, в то время как одна из занятых клеток при этом обязательно освободится. Если величина перераспределяемой поставки равна поставкам не в одной, а в нескольких вершинах контура со знаком "-" (это как раз имеет место в контуре перераспределения в табл. 3.8), то освобождается только одна клетка, обычно с наибольшей стоимостью перевозки, а все другие такие клетки остаются занятыми с нулевой поставкой.

Результат указанных операций для представленного в табл. 3.8 распределения поставок показан в табл. 3.10. Суммарные затраты на перевозки по этому плану составляют:

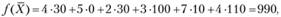
что значительно меньше предыдущей суммы затрат 1170, хотя план перевозок в табл. 3.10 еще не является оптимальным. Об этом свидетельствует наличие отрицательных значений в матрице оценок клеток этого плана (соответствующие потенциалы u_i и v_j найдены способом, изложенным при описании этапа 2):

Таблица 3.10

Мощности поставщиков	Мощности потребителей				ui
	30	100	40	110
60	4 30	5 0	2 30	3	0
100	1	3 100	6	2	2
120	6	2	7 10	4 110	-5
vi	4	5	2	-1

Транспортные задачи, в базисном плане перевозок которых имеют место занятые клетки с нулевой поставкой (или в первоначальном распределении, или в процессе итераций), называются вырожденными; пример такой задачи представлен в табл. 3.10. В случае вырожденной транспортной задачи существует опасность зацикливания, т.е. бесконечного повторения итераций (бесконечного перебора одних и тех же базисных комбинаций занятых клеток). Как правило, в практических задачах транспортного типа зацикливание не встречается, тем не менее следует знать, что существуют специальные правила, позволяющие выйти из цикла, если зацикливание все же произойдет. При отсутствии вырождения метод потенциалов конечен и приводит к оптимальному плану перевозок за конечное число шагов.

Пример 3.4. Решим методом потенциалов закрытую транспортную задачу, заданную в табл. 3.11, в которую уже внесено некоторое допустимое базисное распределение. Суммарные транспортные расходы составляют при этом плане перевозок

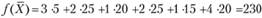
Потенциалы по формуле (3.19) находим следующим образом: задавая u_{ = 0, находим по клетке (1; 1) = 3, по клетке (1; 2) = 2, а по клетке (1; 4) = 1; затем по клетке (2; 1) находим и₂ = 1 и по клетке (2; 3) v₃ = 2; наконец, по клетке (3; 3) находим u₃ = -2.

Таблица 3.11

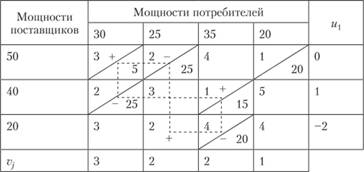
Матрица оценок клеток для этого плана рассчитывается по формуле (3.21):

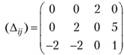
Наличие отрицательных оценок свидетельствует о том, что план неоптимален. Построим контур перераспределения, например, для клетки (3; 2) в табл. 3.11 он показан пунктиром и его вершинам присвоены соответствующие знаки.

Наименьшая поставка в вершине контура со знаком "-" равна 20, поэтому проведем перераспределение поставок, уменьшив поставки в клетках со знаком "-" на 20 и увеличив поставки в клетках со знаком "+" также на 20; при этом клетка (3; 2) заполняется, а клетка (3; 3) освобождается. Новый план представлен в табл. 3.12, соответствующие значения потенциалов показаны в последних столбце и строке.

Таблица 3.12

Мощности поставщиков	Мощности потребителей				ui
	30	25	3	20
50	3 25	2 5	4	1 20	0
40	2 5	3	1 35	5	1
20	3	2 20	4	4	0
vj	3	2	2	1

Матрица оценок клеток этого распределения не содержит отрицательных значений, следовательно, данный план перевозок является оптимальным, стоимость перевозок по этому плану равна

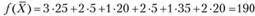
Наличие нулевой оценки незанятой клетки (3;1) говорит о том, что оптимальный план не является единственным. Можно отметить также, что, применяя для начального распределения в этой транспортной задаче модификацию двойного предпочтения метода наименьших стоимостей, мы сразу же получили бы оптимальное распределение, представленное в табл. 3.12.

Пример 3.5. Рассмотрим пример решения открытой транспортной задачи, исходные данные которой представлены в табл. 3.13.

Таблица 3.13

Мощности поставщиков	Мощности потребителей
	30	100	40	100
60	4	5	2	3
100	1	3	6	2
120	6	2	7	4

Проверим выполнение условия баланса (3.18):

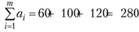
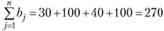
Условие баланса не выполняется, следовательно, задача действительно является открытой. Сформулируем экономико-математическую модель этой задачи.

Пусть Х_y- объемы перевозок от г-го поставщика j-му потребителю. Целевая функция задачи будет иметь вид

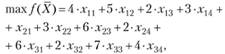
а ограничения выглядят следующим образом: по поставщикам:

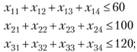
по потребителям: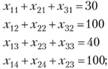

прямые ограничения: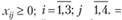

Сведем эту задачу к закрытой, введя фиктивного потребителя с мощностью 280 - 270 = 10; стоимости перевозок единицы груза в соответствующих (фиктивных) клетках принимаются равными нулю, и эти клетки при составлении начального распределения перевозок заполняются в самую последнюю очередь. Начальный план перевозок но методу наименьших стоимостей представлен в табл. 3.14.

Матрица оценок клеток этого плана в соответствии с методом потенциалов имеет вид

Таблица 3.14

Мощности поставщиков	Мощности потребителей					и,
	30	100	40	100	10
60	4	5	2 40	3 20	0	0
100	1 30	3	6	2 70	0	1
120	6	2 100	7	4 70	0 10	-1
	2	1	2	3	-1

Анализ элементов матрицы оценок клеток свидетельствует о том, что план перевозок в табл. 3.14 является оптимальным и единственным. Стоимость перевозок по этому плану составит 550, при этом мощности потребителей будут удовлетворены полностью, а у третьего поставщика останутся невывезенными 10 единиц груза.

Таблица 3.15

Базисные переменные	План	x1	x2	x3	x4
x1	1	1	0	1	-0,5
x2	7,5	0	1	-2	1,26
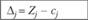
	29,5	0	0	1	0,25

Отсюда видно, что в оптимальном плане х₁, = 1; х₂ = 7,5 и максимум целевой функции равен

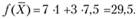
Для нецелочисленной переменной х₂ составляем из приведенной симплексной табл. 3.15 уравнение:

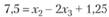
откуда

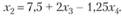
Так как х₂ - целое число, то целой должна быть и правая часть последнего уравнения ("=" - символ конгруэнтности):

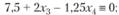
отсюда можно получить, что

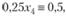
т.е. выражение 0,25х₄ может быть равно 0,5, или 1,5, или 2,5 и т.д. Следовательно, появляется дополнительное ограничение: 0,25х₄ > 0,5, которое путем ввода дополнительной неотрицательной целочисленной переменной х₅ преобразуется в равенство, так что система ограничений исходной задачи в каноническом виде содержит три уравнения:

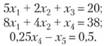
Повторив процесс решения симплексным методом для данной расширенной системы ограничений, получим новый оптимальный план, в котором переменные, входящие в базис, принимают целые значения: х₁ = 2; х₂ = 5; х ₄ = 2. Таким образом, приобретение двух машин типа А и пяти машин типа Б обеспечивает максимум производительности участка, равный 29 тыс. ед. продукции в смену. Заметим, что если бы в качестве плана был выбран вариант, получаемый в результате округления первоначального решения задачи симплексным методом (x₁ = 1; x₂ = 7), то суммарная производительность была бы равна лишь 28 тыс. ед. продукции.

Рассмотрим далее ряд специальных оптимизационных задач, сводящихся к задачам линейного целочисленного программирования. Одной из таких задач является задача о назначениях, с помощью которой можно получить ответ на вопросы типа: как распределить рабочих по станкам, чтобы общая выработка была наибольшей или затраты на заработную плату наименьшими; как наилучшим образом распределить экипажи самолетов; как назначить людей на различные должности (отсюда и название задачи) и т.д.

Математически такие задачи относятся к тому же типу распределительных задач, что и рассмотренная в параграфе 3.2 транспортная задача, с той особенностью, что в них объемы наличных и требующихся ресурсов для выполнения каждой работы равны единице (a_i = b_j = 1), а все переменные x_ij: либо равны единице, если i-й работник назначен на j-ю работу, либо равны нулю в других случаях. Исходные данные задачи о назначениях группируются в таблице, которая называется матрицей оценок, а результаты - в матрице назначений.

Задача о назначениях в общем виде может быть сформулирована следующим образом. Имеется п работников, которые могут выполнять п работ, причем использование г-го работника на j-й работе, например, приносит доход с_ij. Требуется поручить каждому из работников выполнение одной вполне определенной работы, чтобы максимизировать в данном случае суммарный доход.

Введем переменные:

Задача состоит в том, чтобы найти распределение X = (Xjj) работников по работам (т.е. найти матрицу назначений), которое максимизирует целевую функцию

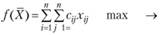(3.22)

при ограничениях

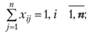(3.23)

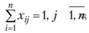(3.24)

причем x_ij равно либо 0, либо 1 (так называемые булевы переменные) для всех i,j = i,n.

Ограничения (3.23) отражают условие того, что за каждым работником может быть закреплена только одна работа, а ограничения (3.24) означают, что для выполнения каждой работы может быть выделен только один работник.

Если в задаче о назначениях элементы матрицы оценок представляют собой, например, время выполнения каждым работником любой из работ, то целевая функция этой задачи будет минимизироваться. Следует заметить также, что при решении задачи о назначениях часто используются алгоритмы и методы решения транспортных задач, в частности метод потенциалов.

Другой задачей подобного рода является задача о коммивояжере, которая может быть сформулирована следующим образом. Имеется п городов, пронумерованных числами от 1 до п. Коммивояжер, выезжая из города 1, должен побывать в каждом городе ровно один раз и вернуться в исходный пункт. Пусть известны расстояния с_ij между городами (i,j = 1,n; i j). Требуется найти самый короткий маршрут.

Введем переменные:

Требование однократного въезда в города и выезда из них запишется в виде следующих ограничений:

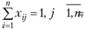(3.25)

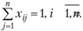
Однако ограничения (3.25) полностью не определяют допустимые маршруты, так как не исключают возможности разрыва пути, т.е. появления нескольких не связанных между собой подмаршрутов для части городов. Поэтому следует ввести дополнительно п переменных и_i (и_i (i = 1, п), принимающих только целые неотрицательные значения, и записать для них специальные ограничения:

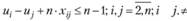(3.26)

Общее число таких ограничений равно (п - 1) · (n - 2), и они, не исключая допустимый маршрут, исключают возможность существования подмаршрутов.

Таким образом, задача о коммивояжере состоит в минимизации целевой функции:

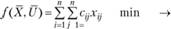(3.27)

при условиях (3.25), (3.26), где переменные Ху, и, принимают только неотрицательные целые значения.

К задачам целочисленного программирования приводят также многие оптимальные задачи теории расписаний, в которой рассматриваются методы оптимизации оперативно-календарного планирования. В качестве примера таких задач можно привести задачу определения оптимальной очередности обработки изделий на различных станках или других рабочих местах, задачу составления программы "диспетчер" для управления работой ЭВМ в мультипрограммном режиме и др.

Рис. 3.3

Максимум функции Z₁ при условиях (3.34) достигается в точке А области Q с координатами (1; 4), так что в данном случае

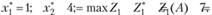
Переходим к максимизации функции Z, при условиях (3.34) и дополнительном ограничении, позволяющем учесть, что по критерию Z, нельзя уступать более чем на δ₁. Так как в нашем примере 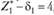, то дополнительное ограничение будет иметь вид

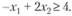(3.35)

Задачу (3.32), (3.34), (3.35) также решаем графически (рис. 3.4).

Получаем, что максимум функции Z₂ при условиях (3.34), (3.35) достигается в точке В части Q, области Q, так что

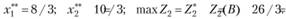
Теперь уступаем по критерию Z₂ на величину уступки 5₂= 5/3 и получаем второе дополнительное ограничение:

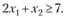(3.36)

Максимизируем функцию Z₃ при условиях (3.34), (3.35) и (3.36). Решение этой задачи представлено на рис 3.5.

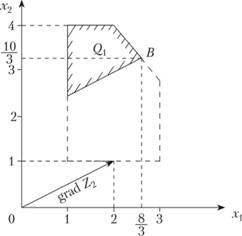
Рис. 3.4

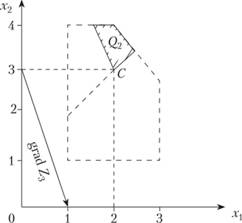
Рис. 3.5

Таким образом, получаем оптимальное решение рассматриваемой трехкритериальной задачи (точка С на рис. 3.5):

x₁ = 2; х₂ = 3.

Соответствующие значения частных критериев при этом составляют:

Z₁ = 4; Z₂ = 7; Z₃ = -7.

Рис. 3.6

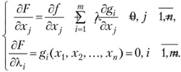(3.42)

В основе метода Лагранжа решения классической задачи оптимизации (3.40), (3.41) лежит утверждение, что если функция 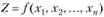в точке 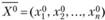имеет экстремум, то существует такой вектор 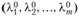, что точка 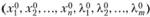является решением системы (3.42). Следовательно, решая систему (3.42), получаем множество стационарных точек, в которых функция Z может иметь экстремальные значения. При этом, как правило, неизвестен способ определения точек глобального максимума или минимума. Однако если решения системы найдены, то для определения глобального максимума или минимума достаточно найти значения функции в соответствующих точках области определения.

Пример 3.9. Найти экстремум функции 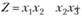при ограничениях

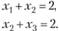
Решение. Составляем функцию Лагранжа

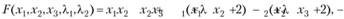
дифференцируем ее по переменным .г₎,х₂,ХзД₎Д2 и полученные выражения приравниваем нулю:

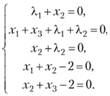
Из первого и третьего уравнений следует, что 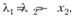поэтому

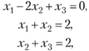
откуда 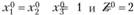. Поскольку, например, точка (0; 2; 0) принадлежит допустимой области и в ней Z = 0, то делаем вывод, что точка (1; 1; 1) - точка глобального максимума.

К классу задач нелинейного программирования, изученному наиболее основательно, относятся задачи с линейными ограничениями и нелинейной целевой функцией. В общем виде такая задача записывается следующим образом:

найти ,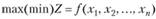

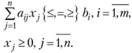
Отметим, что даже для задач с линейными ограничениями вычислительные методы разработаны лишь в тех случаях, когда целевая функция имеет определенные свойства, например, функция Z - сепарабельная, т.е.

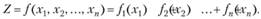
Чтобы гарантировать возможность отыскания оптимального решения, на функции /;(*,) должны быть наложены добавочные ограничения. Другим примером могут служить задачи, в которых целевая функция может быть записана как сумма линейной и квадратичной форм, так что

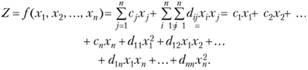
Такие нелинейные задачи называются задачами квадратичного программирования. Чтобы быть уверенным, что оптимальное решение и в этом случае может быть найдено, на величины d_Vj следует наложить некоторые ограничения.

Имеются достаточно эффективные методы решения задачи выпуклого программирования, т.е. задачи минимизации нелинейной, но гладкой выпуклой функции при ограничениях, заданных нелинейными неравенствами, определяющими выпуклое множество переменных:

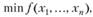(3.43)

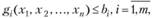(3.44)

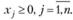(3.45)

В случае максимизации в таких задачах целевая функция должна быть вогнутой. Симплексный алгоритм для решения общей задачи ЛП представляет собой итеративную процедуру, с помощью которой точное оптимальное решение может быть получено за конечное число шагов. Для задач нелинейного программирования вычислительный метод, дающий точное оптимальное решение за конечное число шагов, удается построить не всегда. Здесь часто приходится соглашаться на использование методов, дающих только приближенное решение или требующих для сходимости бесконечного числа шагов.

Один из наиболее мощных методов решения задач нелинейного программирования состоит в преобразовании задачи каким-либо образом к виду, допускающему применение симплексного алгоритма. Природа "преобразования", с помощью которого нелинейная задача может быть приведена к форме, допускающей применение симплексного метода, очень сильно зависит от типа задачи. В некоторых случаях не требуется никакой предварительной аппроксимации, в других аппроксимация нужна. Однако эта аппроксимация может быть сделана сколь угодно точной (ценой увеличения объема вычислений).

Широко применяется градиентный метод. Он представляет собой итеративную процедуру, в которой переходят шаг за шагом от одного допустимого решения к другому так, что значение целевой функции улучшается. Однако в отличие от симплексного метода ЛП в нем не используется переход от одной вершины к другой. Вообще говоря, для сходимости к решению здесь требуется бесконечное число итераций.

Широкое применение нашли методы штрафных функций и барьеров. Метод штрафных функций аппроксимирует задачу с ограничениями задачей без ограничений с функцией, которая налагает штраф за выход из допустимой области.

Идея метода барьеров аналогична методу штрафных функций, однако аппроксимация здесь осуществляется "изнутри" допустимой области.

Весьма полезным вычислительным методом для решения некоторых типов задач нелинейного программирования является метод динамического программирования (ДП). При решении задачи этим методом процесс решения расчленяется на этапы, решаемые последовательно во времени и приводящие, в конечном счете, к искомому решению. Типичные особенности многоэтапных (многошаговых) задач, решаемых методом динамического программирования, состоят в следующем.

o Процесс перехода производственно-экономической системы из одного состояния в другое должен быть марковским (процессом с отсутствием последействия). Это значит, что если система находится в некотором состоянии 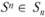, то дальнейшее развитие процесса зависит только от данного состояния и не зависит от того, каким путем система приведена в это состояние.

o Процесс длится определенное число шагов N. На каждом шаге осуществляется выбор одного управления uⁿ, под воздействием которого система переходит из одного состояния Sⁿ в другое 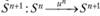. Поскольку процесс марковский, то иⁿ = uⁿ(Sⁿ) зависит только от текущего состояния.

o Каждый шаг (выбор очередного решения) связан с определенным эффектом, который зависит от текущего состояния и принятого решения: φ_n(Sⁿ, uⁿ).

o Общий эффект (доход) за N шагов слагается из доходов на отдельных шагах, т.е. критерий оптимальности должен быть аддитивным (или приводящимся к нему).

Требуется найти такое решение uⁿ для каждого шага (п = 1, 2, 3,..., N), т.е. последовательность (u¹,..., u^N), чтобы получить максимальный эффект (доход) за N шагов.

Любая возможная допустимая последовательность решений (u¹,..., u^N) называется стратегией управления. Стратегия управления, доставляющая максимум критерию оптимальности, называется оптимальной.

В основе общей концепции метода ДП лежит принцип оптимальности Беллмана.

Оптимальная стратегия обладает таким свойством, что независимо от того, каким образом система оказалась в рассматриваемом конкретном состоянии, последующие решения должны составлять оптимальную стратегию, привязывающуюся к этому состоянию. Математически этот принцип записывается в виде рекуррентного соотношения ДП (РДП):

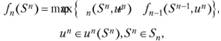
где uⁿ(Sⁿ) - все допустимые управления при условии, что система находится в состоянии Sⁿ;

φ_n(Sⁿ, uⁿ) - эффект от принятия решения uⁿ;

fⁿ(Sⁿ) - эффект за оставшиеся п шагов.

Благодаря принципу оптимальности удается при последующих переходах испытывать не все возможные варианты, а лишь оптимальные выходы. РДП позволяют заменить трудоемкое вычисление оптимума по N переменным в исходной задаче решением N задач, в каждой из которых оптимум находит лишь по одной переменной.

Имеется очень много практически важных задач, которые ставятся и решаются как задачи ДП (задачи о замене оборудования, о ранце, распределения ресурсов и т.д.)

В качестве примера построения РДП рассмотрим использование принципа оптимальности для реализации математической модели задачи оптимального распределения некоторого ресурса в объеме х:

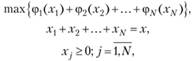
где x_j- количество ресурса, используемое j-м способом;

φ_n(x_j) - доход от применения способа .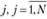

Рекуррентные соотношения, с помощью которых находится решение этой задачи, имеют вид:

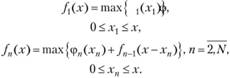
Пример 3.10. Найти максимум функции 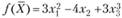при ограничениях

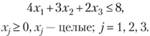
Решение. Целевая функция задачи 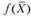является аддитивной, так как ее можно представить в виде суммы функций f_j(x_j), каждая из которых зависит только от одной переменной х_j.

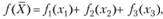
где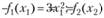

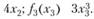
Находим 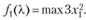Поскольку на переменные x_j накладываются условия целочисленности и неотрицательности, то знак 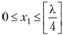(знак [] обозначает целую часть числа, т.е. наибольшее целое число, не превосходящее данное); таким образом, x₁ Î {0,1,2}. Для каждого фиксированного значения l вычисляем значение функции f₁(l) выбираем среди них максимальное, при этом в соответствии с ограничениями задачи X может принимать все целые значения от 0 до 8. Далее вычисляем:

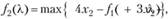
для всех ;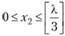

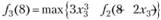
для всех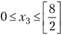

Все вычисления приведены в табл.3.16.

Таким образом, max 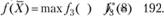Оптимальную стратегию находим следующим образом. Сначала устанавливаем, что 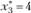(соответствует максимальному значению 192). Значение 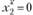находим из соответствующих граф табл. 3.16 для 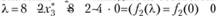при ).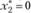

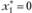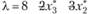
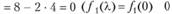Далее находим значение для при 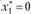). Таким образом, оптимальная стратегия имеет вид (0; 0; 4).

Таблица 3.16

Основные понятия сетевого моделирования

Сетевой моделью (другие названия: сетевой график, сеть) называется экономико-математическая модель, отражающая комплекс работ (операций) и событий, связанных с реализацией некоторого проекта (научно-исследовательского, производственного и др.), в их логической и технологической последовательности и связи. Анализ сетевой модели, представленной в графической или табличной (матричной) форме, позволяет, во-первых, более четко выявить взаимосвязи этапов реализации проекта и, во-вторых, определить наиболее оптимальный порядок выполнения этих этапов в целях, например, сокращения сроков выполнения всего комплекса работ. Таким образом, методы сетевого моделирования можно отнести к методам принятия оптимальных решений.

Математический аппарат сетевых моделей базируется на теории графов. Графом называется совокупность двух конечных множеств: множества точек, которые называются вершинами, и множества пар вершин, которые называются ребрами. Представление о графе можно получить, если рассмотреть некоторый геометрический многогранник, например куб; в кубе можно выделить два конечных множества, состоящих соответственно из восьми вершин и двенадцати ребер.

Если рассматриваемые пары вершин являются упорядоченными, т.е. на каждом ребре задается направление, то граф называется ориентированным; в противном случае - неориентированным. Последовательность неповторяющихся ребер, ведущая от некоторой вершины к другой, образует путь. Граф называется связным, если для любых двух его вершин существует путь, их соединяющий; в противном случае граф называется несвязным. В экономике чаще всего используется два вида графов: дерево и сеть. Дерево представляет собой связный граф без циклов, имеющий исходную вершину (корень) и крайние вершины; пути от исходной вершины к крайним вершинам называются ветвями. Сеть - это ориентированный конечный связный граф, имеющий начальную вершину (источник) и конечную вершину (сток). Таким образом, сетевая модель представляет собой граф вида "сеть".

В экономических исследованиях сетевые модели возникают при моделировании экономических систем и процессов методами сетевого планирования и управления (СНУ).

Объектом управления в системах сетевого планирования и управления являются коллективы исполнителей, располагающие определенными ресурсами и выполняющие заданный комплекс операций, который призван обеспечить достижение намеченной цели, например разработку нового изделия, строительство объекта и т.п.

Основой СНУ служит сетевая модель (СМ), в которой моделируется совокупность взаимосвязанных работ и событий, отображающих процесс достижения определенной цели. Она может быть представлена в виде графика или таблицы.

Основными понятиями СМ являются следующие: работа, событие, путь. На рис. 3.7 графически представлена СМ, состоящая из 5 событий (кружочки) и 6 работ (стрелки); продолжительность выполнения работ в некоторых единицах времени указана над стрелками.

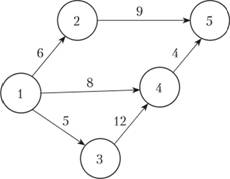
Рис. 3.7. Сетевая модель

Работа характеризует материальное действие, требующее использования ресурсов, или логическое, требующее лишь взаимосвязи событий. При графическом распределении работа изображается стрелкой, которая соединяет два события. Ома обозначается парой заключенных в скобки чисел (i,j), где i - номер события, из которого работа выходит, a j - номер события, в которое она входит. Работа не может начаться раньше, чем свершится событие, из которого она выходит. Каждая работа имеет определенную продолжительность t(i,j). Например, запись t(2, 5) = 9 означает, что работа (2, 5) имеет продолжительность 9 единиц времени (см. рис. 3.7). К работам относятся также такие процессы, которые не требуют ни ресурсов, ни времени выполнения. Они заключаются в установлении логической взаимосвязи работ и показывают, что одна из них непосредственно зависит от другой и не может выполняться, прежде чем эта другая будет завершена; такие работы называются фиктивными и на графике изображаются пунктирными стрелками.

Событиями называются результаты выполнения одной или нескольких работ. Они не имеют протяженности во времени. Событие свершается в тот момент, когда оканчивается последняя из работ, входящая в него. События обозначаются одним числом и при графическом представлении СМ изображаются кружком (или иной геометрической фигурой), внутри которого проставляется его порядковый номер (i = 1, 2,... N). В СМ имеется начальное событие (с номером 1), из которого работы только выходят, и конечное событие (с номером N), в которое работы только входят.

Путь в СМ - это цепочка следующих друг за другом работ, соединяющих начальную и конечную вершины, например, в приведенной на рис. 3.7 модели путями являются L₁ = (1, 2, 5), L₂ = (1, 4, 5) и др. Продолжительность пути определяется суммой продолжительностей составляющих его работ. Путь, имеющий максимальную длину, называют критическим и обозначают L_кр, а его продолжительность - t_кр Работы, принадлежащие критическому пути, называются критическими. Их несвоевременное выполнение ведет к срыву сроков всего комплекса работ.

Таблица 3.17

Kпр	(i, j)	t(i, j)	tpн(i, j) = tp(i, j)	tpo(i, j)	tпн(i, j)	tпо(i, j) = tп(i, j)	Rп	Rн	Кн
1	2	3	4	5 = 4 + 3	6 = 7 - 3	7	8	9	10
0	(1,2)	6	0	6	0	6	0	0	0,71
0	(1,3)	0	0	Э	0	0	0	0	1
0	(1,4)	8	0	8	9	17	9	9	0,47
1	(2,5)	9	6	15	12	21	6	0	0,71
1	(3,4)	12	0	17	0	17	0	0	1
2	(4,5)	4	17	21	17	21	0	0	1

Этап 3. Заполнение таблицы начинается с расчета раннего срока работ t_p(i). Для работ, имеющих цифру "ноль" в первой графе, в графе 4 также заносятся нули и рассчитываются соответствующие значения для графы 5 (ранний срок окончания как суммы соответствующих чисел в графе 4 и графе 3 (см. формулу (3.51)). В нашей модели таких работ три; в первой строчке графы 5 ставим 0 + 6 = 6, аналогично по второй и третьей строке.

Для заполнения следующих строк графы 4 для работ (i,j) просматриваются заполненные строки графы 5, содержащие работы, оканчивающиеся на номер i, и максимальное из найденных значений (если их несколько) переносится в графу 4 для обрабатываемых строк. Так, в нашем примере в четвертой строке в графе 4 ставим 6, а в графе 5 - 15 (6 + 9 = 15). Аналогично в пятой строке в графе 4 и графе 5 ставим соответственно 5 и 17 (5 + 12 = 17). В последней шестой строке в графе 4 ставим 17 (наибольшее из чисел 8 и 17 в графе 5) и соответственно в графу 5 ставим 21 (17 + 4 = 21).

Этап 4. Графы 7 и 6 заполняются "обратным ходом", т.е. снизу вверх. Для этого просматриваются строки (работы), оканчивающиеся на номер N последнего события, и из графы 5 выбирается максимальная величина; эта величина записывается в графу 7 по всем строчкам, оканчивающимся на N (см. формулу (3.51)), с учетом равенства t_п (N) = t_p(N). Затем заполняется графа 6 по этим строкам как разность между графой 7 и графой 3 (см. формулу (3.52)). В нашем примере таких строк две (четвертая и шестая), для которых в графе 5 стоят числа 15 и 21; выбираем наибольшее из них (21) и записываем его в графу 7 по этим строкам, после чего заносим соответствующие числа в графу 6.

Далее просматриваются строки, оканчивающиеся на номер события, предшествующего завершающему, т.е. на (N - 1). Для этих строк просматриваются все строчки графы 6, лежащие ниже и начинающиеся с номера (N - 1); среди них в графе 6 выбирается минимальная величина, которая переносится в графу 7 по обрабатываемым строкам, после чего заполняется графа 6. В нашем примере таких строк две (третья и пятая); ниже их с номера 4 начинается одна (последняя) работа, и в графе 6 стоит 17, следовательно, в графе 7 по этим строчкам ставим число 17, после чего заполняется графа 6.

Затем аналогичный процесс повторяется для строк, оканчивающихся на (N - 2), (N - 3) и т.д. до тех пор, пока не будут заполнены все строки по графы 7 и 6. В нашем примере результаты приведены в соответствующих графах табл. 3.17.

Этап 5. Показатели графы 8 рассчитываются как разности соответствующих показателей граф 6 и 4 или граф 7 и 5 (см. формулы (3.48) или (3.53)). Чтобы заполнить графу 9, можно предварительно рассчитать резервы времени каждого события по формуле (3.48), а затем воспользоваться формулой (3.55). В нашем примере резервы времени для каждого из пяти событий равны соответственно: R(1) = 0; R(2) = 12 - 6 = 6; R(3) = 5 - 5 = 0; R(4) = 17 - 17 = 0; R(5) = 0. Последующие результаты по формуле (3.55) приведены в графе 9 табл. 3.17.

Этап 6. На этом этапе подводятся основные итоги расчета. Учитывая, что нулевой резерв времени имеют только работы (R_п = 0) и события (R(i) = 0), которые принадлежат критическому пути, получаем, что критическим является путь L_Kp = (1, 3, 4, 5), продолжительность которого (t_кр) равна 21 дню. Так как работы (1, 2), (1, 4) и (2, 5) имеют ненулевые резервы R_п, то очевидно, что путем перевода некоторого числа рабочих с этих работ на работы, принадлежащие критическому пути, можно сократить продолжительность этого пути и тем самым сократить сроки выполнения проекта в целом, т.е. осуществить оптимизацию сетевого графика.

Оптимизация сетевых моделей

Для оптимизации сетевой модели, выражающейся в перераспределении ресурсов с ненапряженных работ на критические для ускорения их выполнения, необходимо как можно более точно оценить степень трудности своевременного выполнения всех работ, а также "цепочек" пути. Более точным инструментом решения этой задачи по сравнению с полным резервом является коэффициент напряженности, который может быть вычислен одним их двух способов в соответствии с приведенной ниже формулой:

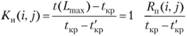(3.56)

где t(L_max) - продолжительность максимального пути, проходящего через работу (i, j);

t'_кp- общая продолжительность отрезков пути, проходящего через работу (i, j), совпадающих с критическим путем.

Коэффициент напряженности изменяется от нуля до единицы, причем чем он ближе к единице, тем сложнее выполнить данную работу в установленный срок. Самыми напряженными являются работы критического пути, для которых коэффициент напряженности равен 1. На основе значений этого коэффициента все работы СМ могут быть разделены на три группы:

- напряженные (K_н(i,j) > 0,8);

- подкритические (0,6 < K_n(i,j) < 0,8);

- резервные (K_н(i,j) < 0,6).

В результате перераспределения ресурсов стараются максимально уменьшить общую продолжительность работ, что возможно при переводе всех работ в первую группу.

Пример 3.12. Рассчитаем коэффициенты напряженности всех работ сетевой модели, рассматриваемой выше в примере 3.11. При расчете этих показателей по формуле (3.56) целесообразно пользоваться графиком данной СМ, представленным на рис. 3.7. Для работ критического пути (1, 3), (3, 4) и (4, 5) коэффициенты напряженности К_н = 1. Для других работ:

К_н(1, 2) = 1 - (6: (21 - 0)) = 0,71;

К_н(1, 4) = 1 - (9: (21 -4)) = 0,47;

К_н(2, 5) = 1 - (6 : (21 - 0)) = 0,71.

Результаты расчетов приведены в графе 10 (К_н) табл. 3.17. Они показывают, что напряженными являются работы критического пути (1, 3), (3, 4) и (4, 5); работы (1, 2) и (2, 5) являются подкритическими, а работа (1, 4) - резервная. Следовательно, оптимизация рассматриваемой СМ возможна в основном за счет резервной работы (1, 4) и частично за счет подкритических работ (1,2) и (2, 5).

Если данный расчет СМ проведен до начала работ, менеджер проекта может скорректировать первоначальное распределение рабочих по видам работ, сняв некоторое количество рабочих с работы (1, 4) и, возможно, с работ (1, 2) и (2, 5) и распределив их по работам критического пути (1, 3), (3, 4) и (4, 5).

В результате работы, не лежащие на критическом пути, несколько увеличат свою продолжительность, а продолжительность работ критического пути сократится; тем самым при той же численности рабочих сократится срок реализации проекта в целом. Получив новый вариант сетевого графика, менеджер может повторить аналогичные расчеты, добиваясь путем перераспределения рабочих наиболее оптимального варианта СМ и, следовательно, наилучшего распределения рабочих по видам работ.

Сетевое планирование в условиях неопределенности

В рассмотренных выше примерах сроки выполнения отдельных видов работ определялись при условии взаимозаменяемости рабочих и при наличии нормативов трудоемкости для данных работ. на практике во многих случаях трудно точно определить продолжительность работ, поэтому задаются две оценки этой продолжительности - минимальная и максимальная. Минимальная оценка t_min(i,j) дает продолжительность работ при наиболее благоприятных обстоятельствах, а максимальная t_max(i,j) - при наиболее неблагоприятных. Продолжительность работы в этом случае рассматривается как случайная величина, которая при реализации может принять любое значение в заданном интервале. Такие оценки являются вероятностными, и их ожидаемые значения t_ож(i,j) оцениваются по-разному в зависимости от принятого закона распределения. Так, при бета-распределении плотности вероятности ожидаемое значение продолжительности работ (математическое ожидание) задается формулой

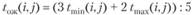(3.57)

Для характеристики степени разброса возможных значений относительно ожидаемого уровня используется показатель дисперсии:

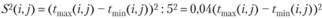(3.58)

На основе этих оценок можно рассчитать все характеристики СМ, однако они будут выступать как средние характеристики. При достаточно большом количестве работ можно утверждать, что общая продолжительность любого пути, включая критический, имеет нормальный закон распределения со средним значением, равным сумме средних значений продолжительности составляющих его работ, и дисперсией, равной сумме дисперсий этих же работ.

Кроме основных характеристик СМ, при вероятностном задании продолжительности работ можно решить две важные задачи:

1. определить вероятность того, что продолжительность критического пути t_кp не превысит заданного (директивного) уровня Т;

2. определить максимальный срок выполнения всего комплекса работ Т при заданном уровне вероятности (надежности) р.

Более подробно вопросы сетевого планирования в условиях неопределенности с решением конкретных примеров рассмотрены в ряде учебных и научных изданий (см. например, параграф 3.6 в [15]).

 

Лекция 3 Оптимизационные экономико-математические модели

- Теория двойственности в анализе оптимальных решений экономических задач

- Транспортная задача

- Целочисленное программирование

- Задачи многокритериальной оптимизации

- Нелинейное и динамическое программирование; понятие об имитационном моделировании

- Модели сетевого планирования и управления

В результате изучения материала этой главы студенты должны:

знать:

o основные понятия теории двойственности линейного программирования;

o методы формулировки и решения транспортных задач;

o особенности методов целочисленного, нелинейного, динамического программирования и имитационного моделирования;

o принципы и методы использования сетевых моделей в экономике;

уметь:

o использовать при анализе оптимальных решений теоремы двойственности;

o решать закрытые и открытые транспортные задачи;

o применять методы целочисленного и многокритериального программирования при решении практических задач;

o строить сетевые модели и оптимизировать их;

владеть:

o понятийным аппаратом теории двойственности;

o практическими навыками постановки и решения транспортных задач, задач целочисленного программирования и многокритериальной оптимизации, задач сетевого планирования и управления.