Проекция силы на ось и на плоскость

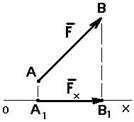
Проекция силы на ось. Пусть сила F образует с осью OX угол a (рис. 2.1), тогда проекция этой силы на ось будет:

F_x = Fcosa.

Проекция силы на ось есть величина скалярная.

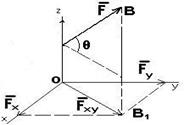Проекция силы на плоскость. Проекцией силы F на плоскость OXY называется вектор F_xy = OB₁, заключенный между проекциями начала и конца силы F на эту плоскость (рис. 2.2.)

Проекция силы на плоскость есть величина векторная, так как она кроме численного значения характеризуется направлением на плоскости. По модулю F_xy = Fcosq, где q - угол между направлением силы F и ее проекцией F_xy.

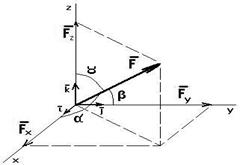Аналитический способ задания сил. Для аналитического способа задания силы необходимо выбрать систему координат OXYZ и спроектировать силу на оси координат (рис. 2.3).

Направляющие косинусы определяются по формулам:

        

 .           

                                                          .

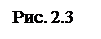
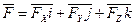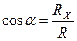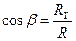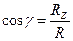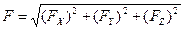Для плоской системы сил:

; ; ; .

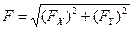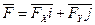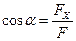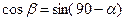Аналитический способ сложения сил

Теорема: проекция вектора суммы на какую-нибудь ось равна алгебраической сумме проекций слагаемых векторов на ту же ось.

Если R = F₁ + F₂ + F₃ + … + F_n, причем (F_1x, F_1y, F_1z), (F_2x, F_2y, F_2z), …, (F_3x, F_3y, F_3z) – наборы проекций этих векторов на оси X, Y и Z то

R_x = F_1x + F_2x + F_3x + … + F_nx = åF_ix;

R_y = F_1y + F_2y + F_3y + … + F_ny = åF_iy;

R_z = F_1z + F_2z + F_3z + … + F_nz = åF_iz;

Модуль результирующей силы:

.

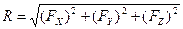Направление результирующего вектора R определяется направляющими косинусами:

; ; .

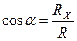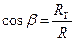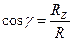Пример 1. Определить результирующую силу трех сил F₁, F₂, F₃ проекции которых заданы: F₁(3;3), F₂(6;-2), F₃(-5;-3). Силы заданы в Ньютонах (рис. 2.4).

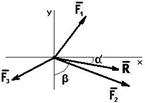Решение:

R_x = 3 + 6 – 5 = 4H; R_y = 3 – 2 – 3 = -2H;

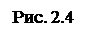
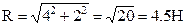Направляющие косинусы:

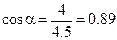
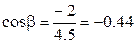
Ответ: R = 4,5H; a = 63^o; b = 27^o.

Пример 2. Задана плоская система сил, действующая на точку А. F₁ = 15Н; F₂ = 10Н. Определить равнодействующую силу (рис. 2.5).

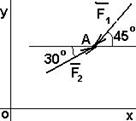Решение:

Определим сумму проекций данных сил на оси OX и OY:

Ось OX: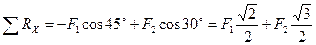

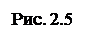Ось OY: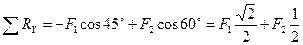

Подставляя численные значения получим:

                                åR_x = 19,1Н; åR_y = -5,5Н.

Модуль равнодействующей: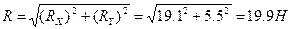

Направляющие косинусы: ; .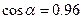

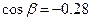Ответ: R = 19,9H; a = 74^o; b = 16^o.

Равновесие системы сходящихся сил

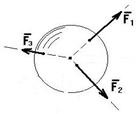
Система сходящихся сил – это силы, сходящиеся в одной точке (рис. 2.6).

Геометрическое условие равновесия. Для равновесия системы сходящихся сил необходимо и достаточно, чтобы силовой многоугольник, построенный на этих силах, был замкнут.

Аналитические условия равновесия. Для равновесия пространственной системы сходящихся сил необходимо и достаточно, чтобы суммы проекций этих сил на каждую из трех координатных осей были равны нулю.

åF_kx = 0; åF_ky = 0; åF_kz = 0.

Теорема о трех силах. Если свободное твердое тело находится в состоянии равновесия под действием трех непараллельных сил, лежащих в одной плоскости, то линии действия этих сил пересекаются в одной точке.

F₁ + F₂ + F₃ = 0