Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

1. Гладкая поверхность

Реакция связи N гладкой поверхности или опоры направлена по нормали к поверхностям соприкасающихся тел в точке касания и приложена в этой точке.

                                                       а)                    б)                    в)

                                    Рис. 1.5

 Если одна из соприкасающихся поверхностей является точкой, то реакция направлена по нормали к другой поверхности (рис. 1.5).

2. Нить, стержень.

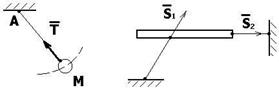Реакция Т натянутой нити и нагруженного стержня S направлена вдоль этих связей и приложена в точке контакта (рис. 1.6).

 

а)                    б)

        Рис. 1.6

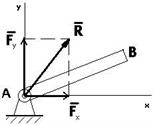3. Цилиндрический шарнир (подшипник, петля).

Реакция R цилиндрического шарнира лежит в плоскости, перпендикулярной оси шарнира, и может иметь любое направление в этой плоскости. Для определения R ее раскладывают на два взаимноперпендикулярных направления: R_x и R_y (рис. 1.7).

 

Рис. 1.7

 

 

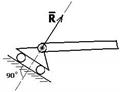4. Подвижная шарнирная опора.

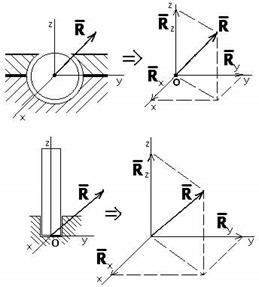
Реакция связи R направлена перпендикулярно плоскости возможного перемещения шарнира (рис. 1.8).

 

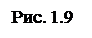
5. Шаровый шарнир и подпятник (рис. 1.9, рис. 1.10).

                                    а)                    б)

                                              Рис. 1.10

Реакция шарового шарнира и подпятника может иметь любое направление в пространстве.

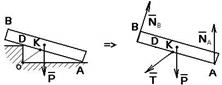
Аксиома связей. Всякое несвободное тело можно рассматривать как свободное, если отбросить связи и заменить их действие реакциями этих связей (рис. 1.11).

Сложение сил

Геометрический способ сложения сил

Величина, равная геометрической сумме сил какой-либо системы называется главным вектором этой системы сил.

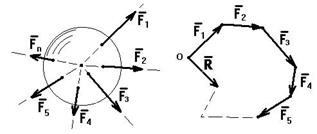
Пусть на твердое тело действует плоская система сил (F₁, F₂, F₃, …, F_n) (рис. 1.12).

Из произвольно выбранной точки О откладывается вектор F₁, из его конца откладывается вектор F₂ и т.д. Вектор R, замыкающий силовой многоугольник, является результирующим:

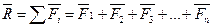
Сложение двух сил

Пусть на тело действуют две силы, лежащие в одной плоскости (рис. 1.13).

.

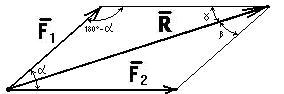
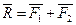
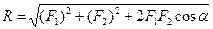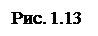Результирующая сила определяется по правилу параллелограмма, модуль силы определяется по теореме косинусов или синусов:

; .

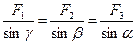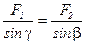Сложение трех сил не лежащих в одной плоскости

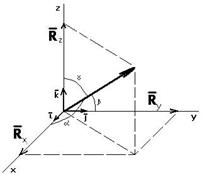Рассмотрим три силы 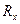, , 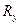 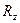не лежащие в одной плоскости (рис. 1.14). Результирующая сила  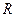равна:

.

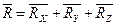Направление силы определим по направляющим косинусам:

;       ;  .

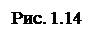
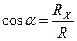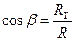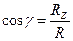Разложение сил

 

Разложение сил по двум заданным направлениям

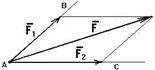Пусть надо силу F разложить по направлениям AB и AD (рис. 1.15).

.

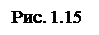
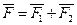Задача сводится к построению параллелограмма, у которого стороны расположены по направлениям AB и AD и данная сила F является диагональю. Тогда стороны параллелограмма будут искомыми силами.

Разложение сил по трем заданным направлениям.

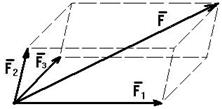
Пусть направления силы не лежат в одной плоскости. Тогда задача сводится к построению параллелепипеда, у которого диагональю является данная сила, а ребра параллельны заданным направлениям (рис. 1.16).

 

.

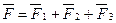Вопросы для самоконтроля

1. Что изучает статика?

2. Что такое абсолютно твердое тело?

3. Основные виды связей и их реакции?

4. Геометрическое сложение сил?

 

Задачи, рекомендуемые для самостоятельного решения: 1.1 – 1.6 [2]

Литература: [1], [3], [4].

 

 

Лекция 2.