· Ток при размыкании R-L – цепочки (при отключении источника тока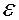 
без разрыва цепи, см. рис. 4.13):
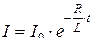, или 
,
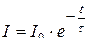где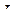 
– сила тока в цепи при t =0, t – время, прошедшее с момента размыкания цепи, R – активное сопротивление цепи, L – индуктивность цепи; 
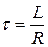– постоянная времениR - L – цепочки.
· Ток при замыкании R-L – цепочки (рис. 4.14, R – активное сопротивление цепи, L – индуктивность цепи):
.
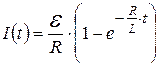· Закон сохранения энергии для идеального колебательного контура (контур без активного сопротивления, R =0, см. рис. 4.15):
.
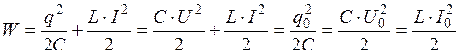Здесь L – индуктивность контура; С – его электроёмкость.
· Дифференциальное уравнение гармонических колебаний для контура без активного сопротивления (рис.4.15):
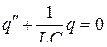, или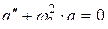 
,
где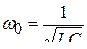 
– циклическая частота свободных колебаний («собственная частота»).
· Зависимость заряда на конденсаторе от времени для свободных колебаний в контуре без сопротивления (рис. 4.15):
.
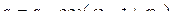· Формула Томсона. Период собственных колебаний в контуре без активного сопротивления (рис. 4.15):
.
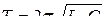· Длина волны, на которую настроен колебательный контур:
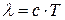, или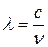 
.
Здесь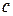 
– скорость распространения электромагнитных волн в вакууме; 
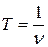– период колебаний, 
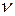– частота.
· Скорость распространения электромагнитных волн в среде с диэлектрической проницаемостью среды, равной ε, и магнитной проницаемостью, равной μ:
.
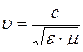· Дифференциальное уравнение затухающих колебаний для контура, содержащего ёмкость C, индуктивность L и активное сопротивление R (рис. 4.16):
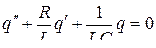, или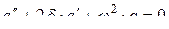 
.
Здесь q – заряд конденсатора,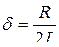 
– коэффициент затухания, 
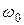– собственная частота.
· Зависимость заряда на конденсаторе от времени для затухающих колебаний в контуре с активным сопротивлением (рис. 4.16, 4.17):
.
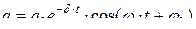· Циклическая частота затухающих колебаний:
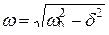, или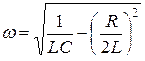 
.
· Зависимость амплитуды затухающих колебаний от времени (рис. 4.17):
.
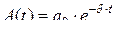· Логарифмический декремент затухания (смысл обозначений см. на рис. 4.17):
.
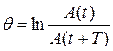· Связь логарифмического декремента и коэффициента затухания
.
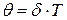· Добротность колебательного контура:
.
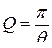При не слишком большом затухании, то есть при δ<<ω0:
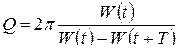, или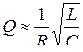 
.
Добротность обратно пропорциональна относительной убыли энергии W колебаний за время, равное одному периоду.
 |
Задачи к разделу 4
241. Бесконечно длинный провод с током I =100 А изогнут так, как показано на рис. 4.18. Определить магнитную индукцию В в точке О. Радиус дуги R=10 см.
242. Магнитный момент pm тонкого проводящего кольца pm=5 A ∙м2. Определить магнитную индукцию В в точке А, находящейся на оси кольца и удаленной от точек кольца на расстояние r=20 см (рис. 4.19).
243. По двум скрещенным под прямым углом бесконечно длинным проводам текут токи I и 2I (I =100 A). Определить магнитную индукцию В в точке А (рис. 4.20). Расстояние d=10 см.
244. По бесконечно длинному проводу, изогнутому так, как это показано на рисунке 4.21, течёт ток I =200 A. Определить магнитную индукцию В в точке О. Радиус дуги R =10 см.
245. По тонкому кольцу радиусом R=20 см течет ток I=100 A. Определить магнитную индукцию В на оси кольца в точке А (рис. 4.22). Угол β = π/3.
246. По двум бесконечно длинным проводам, скрещенным под прямым углом, текут токи I 1 и I 2 =2 I 1 (I 1=100 А). Определить магнитную индукцию В в точке А, равноудаленной от проводов на расстояние d = 10 см (рис. 4.23).
247. По бесконечно длинному проводу, изогнутому так, как это показано на рис. 4.24, течет ток I =200 A. Определить магнитную индукцию В в точке О. Радиус дуги R =10 см.
248. По тонкому кольцу течёт ток I=80 A. Определить магнитную индукцию В на оси кольца в точке А, равноудаленной от точек кольца на расстояние r =10 см (рис. 4.25). Угол α = π/6.
249. По двум бесконечно длинным прямым параллельным проводам текут одинаковые токи I=60 A. Определить магнитную индукцию В в точке А, равноудаленной от проводов на расстояние d=10 см (рис. 4.26). Угол β = π/3.
250. Бесконечно длинный провод с током I=50 A изогнут так, как это показано на рис. 4.27. Определить магнитную индукцию В в точке А, лежащей на биссектрисе прямого угла на расстоянии d=10 см от его вершины.
251. По контуру в виде равностороннего треугольника идёт ток I=40 A. Длина стороны треугольника а=30 см. Определить магнитную индукцию В в точке пересечения высот.
252. По контуру в виде квадрата идёт ток I=50 A. Длина стороны квадрата а=30 см. Определить магнитную индукцию В в точке пересечения диагоналей.
253. По тонкому проводу, изогнутому в виде прямоугольника, течёт ток I=60 A. Длины сторон прямоугольника равны а=30 см и b=40 см. Определить магнитную индукцию В в точке пересечения диагоналей.
254. Тонкий провод изогнут в виде правильного шестиугольника. Длина стороны шестиугольника d=10 см. Определить магнитную индукцию В в центре шестиугольника, если по проводу течёт ток I=25 A.
255. По двум параллельным проводам длиной l=3 м каждый текут одинаковые токи I=500 A. Расстояние между проводами d=10 см. Определить силу взаимодействия проводов. Считать l>>d.
256. По трём прямым параллельным проводам, находящимся на одинаковом расстоянии а=10 см друг от друга, текут одинаковые токи I=100 A. В двух проводах направления токов совпадают. Определить силу, действующую на отрезок длиной l=1 м каждого провода.
257. По двум тонким проводам, изогнутым в виде кольца радиусом R=10 см, текут одинаковые токи I=10 A (рис. 4.28). Найти силу взаимодействия этих колец, если плоскости, в которых лежат кольца, параллельны, а расстояние между центрами колец d=1 мм.
258. По витку радиусом R=5 см течет ток I=10 A. Чему равен магнитный момент pm кругового тока?
259. Короткая катушка содержит N=1000 витков тонкого провода. Катушка имеет квадратное сечение со стороной а=10 см. Найти магнитный момент катушки при силе тока I=1 A.
260. Тонкое кольцо радиусом R=10 см несёт заряд q=10 нКл. Кольцо равномерно вращается с частотой ν=10 с-1 относительно оси, перпендикулярной плоскости кольца и проходящей через его центр. Определить магнитный момент pm, обусловленный вращением кольца.
261. Проволочный виток радиусом R=5 см находится в однородном магнитном поле напряженностью H=2 кА/м. Плоскость витка образует угол α=60° с направлением поля. По витку течет ток силой I=4 A. Найти вращающий момент М, действующий на виток.
262. Короткая катушка площадью поперечного сечения S=150 см2, содержащая N=200 витков провода, по которому течёт ток I=4 A, помещена в однородное магнитное поле напряженностью H=8 кА/м. Определить магнитный момент pm катушки, а также вращающий момент М, действующий на нее со стороны поля, если ось катушки составляет угол α=60° с линиями поля.
263. По квадратной проволочной рамке со стороной а=12 см течёт ток I=3,5 A. Найти напряжённость магнитного поля H на расстоянии h=27 см от плоскости рамки на перпендикуляре к её плоскости, проведённом через центр рамки.
264. По квадратной проволочной рамке со стороной а=38 см течёт ток. Напряженность магнитного поля на расстоянии h=27 см от плоскости рамки на перпендикуляре к её плоскости, проведенном через центр рамки, H=0,29 А/м. Определить ток I.
265. Ион с зарядом q =6∙ e (e – элементарный заряд) и массой M =12∙ m (m – масса протона) ускоряется разностью потенциалов U=6,7 кВ и влетает в однородное магнитное поле напряжённостью H=9,2 кА/м перпендикулярно его силовым линиям. Определить радиус R траектории иона.
266. Ион с зарядом e (e – элементарный заряд) и массой M =2∙ m (m – масса протона) ускоряется разностью потенциалов U и влетает в однородное магнитное поле напряженностью H=19 кА/м перпендикулярно его силовым линиям. Траектория иона имеет радиус R=75 см. Определить U.
267. Ион с зарядом e (e – элементарный заряд) и массой m (m – масса протона), энергия которого равна W, влетает в однородное магнитное поле напряжённостью H=21 кА/м под углом φ=80° к направлению силовых линий. Шаг винтовой линии, по которой ион движется в поле, равен h=45 см. Определить энергию иона W.
268. Частица с зарядом e (e – элементарный заряд) и массой m (m – масса протона) влетает в однородное магнитное поле с индукцией В=0,3 Тл со скоростью υ=1400 км/с под углом φ=35° к направлению поля. Определить радиус R винтовой линии, по которой движется частица.
269. Перпендикулярно магнитному полю с индукцией В=0,1 Тл возбуждено электрическое поле напряженностью Е=100 кВ/м. Перпендикулярно магнитному и электрическому полям движется, не отклоняясь от прямолинейной траектории, заряженная частица. Вычислить скорость частицы υ.
270. Два иона разных масс с одинаковыми зарядами влетели в однородное магнитное поле и стали двигаться по окружностям радиусами R1=3 см и R2=6 см. Определить отношение масс ионов, если они прошли одинаковую ускоряющую разность потенциалов.
271. Одноразрядный ион натрия прошёл ускоряющую разность потенциалов U=1 кВ и влетел перпендикулярно линиям магнитной индукции в однородное поле (В=0,5 Тл). Определить относительную молекулярную массу иона, если он описал окружность радиусом R=4,37 см.
272. Электрон прошёл ускоряющую разность потенциалов U=800 В и, попав в однородное магнитное поле В=47 мТл, стал двигаться по винтовой линии с шагом h=6 см. Определить радиус R винтовой линии.
273. Ион, несущий один элементарный заряд, движется в однородном магнитном поле с индукцией В=15 мТл по окружности радиусом R=10 см. Чему равен импульс p иона?
274. Электрон движется в магнитном поле с индукцией В=2 мТл по окружности радиусом R=1 см. Какова кинетическая энергия электрона в джоулях и в электрон-вольтах?
275. Заряженная частица, обладающая скоростью υ=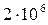 
м/с, влетела в однородное магнитное поле с индукцией В=0,52 Тл. Найти отношение заряда частицы к её массе, если частица в поле описала дугу окружности радиусом R=4 см. Какая это частица?
276. Определить частоту обращения электрона по круговой орбите в магнитном поле, магнитная индукция которого В=0,2 Тл.
277. Электрон движется в однородном магнитном поле с индукцией В=100 мкТл по винтовой линии. Чему равна скорость электрона, если шаг винтовой линии h=20 см, а радиус R=5 см?
278. В однородном магнитном поле с индукцией В=2 Тл движется протон. Траектория его движения представляет собой винтовую линию с радиусом R=10 см и шагом h=60 см. Какова кинетическая энергия протона?
279. На длинный картонный каркас диаметром D=0,05 м уложена однослойная обмотка (виток к витку) из проволоки диаметром d= 
м. Определить магнитный поток, создаваемый таким соленоидом при силе тока 0,5 А.
280. Соленоид длиной l=1 м и сечением S= 
см2 содержит 2000 витков. Вычислить потокосцепление при силе тока в обмотке 10 А.
281. Соленоид содержит 1000 витков. Сила тока в его обмотке 1 А, магнитный поток через поперечное сечение соленоида 
. Вычислить энергию магнитного поля.
282. Соленоид содержит 4000 витков провода, по которому течёт ток 20 А. Определить магнитный поток и потокосцепление, если индуктивность L=0,4 Гн.
283. Плоский контур S=20 см2 находится в однородном магнитном поле с индукцией В=0,03 Тл. Определить магнитный поток Ф, пронизывающий контур, если его плоскость составляет угол φ=60° с направлением линий индукции.
284. Магнитный поток сквозь сечение соленоида Ф=50 мкВб. Длина соленоида l=50 см. Найти магнитный момент pm соленоида, если его витки плотно примыкают друг к другу.
285. Квадратный контур со стороной а=10 см, в котором течёт ток I=6 А, находится в магнитном поле В=0,8 Тл под углом α=50° к линиям индукции. Какую работу нужно совершить, чтобы при неизменной силе тока в контуре изменить его форму на окружность?
286. Плоский контур с током I=5 А и S=20 см2 свободно устанавливается в однородном магнитном поле с индукцией В=0,4 Тл. Поддерживая ток в контуре неизменным, его повернули относительно оси, лежащей в плоскости контура, на угол α=40°. Определить совершённую при этом работу.
287. На картонный каркас длиной l=50 см и площадью сечения S=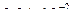 
м2 намотан в один слой провод диаметром d= м так, что витки плотно прилегают друг к другу. Определить индуктивность получившегося соленоида.
288. Индуктивность соленоида, намотанного в один слой на немагнитный каркас, L= 
Гн. Длина соленоида l=0,6 м, диаметр d =0,02 м. Определить число витков, приходящихся на единицу длины соленоида.
289. Плоский контур площадью S=300 см2 находится в однородном магнитном поле с индукцией В=0,01 Тл. Плоскость контура перпендикулярна линиям индукции. В контуре поддерживается неизменный ток I =10 А. Определить работу внешних сил по перемещению контура с током в область пространства, в которой магнитное поле отсутствует.
290. Виток, по которому течёт ток I =20 А, свободно установился в однородном магнитном поле с индукцией В=0,016 Тл. Диаметр витка d =10 см. Определить работу, которую нужно совершить, чтобы повернуть виток на угол 90° относительно оси, совпадающей с диаметром.
291. Виток, в котором поддерживается постоянная сила тока I =60 А, свободно установился в однородном магнитном поле с индукцией В=20 мТл. Диаметр витка d =10 см. Определить работу, которую нужно совершить, чтобы повернуть виток на угол π/3 относительно оси, совпадающей с диаметром.
292. В однородном магнитном поле перпендикулярно линиям индукции расположен плоский контур площадью S=100 см2. Поддерживая в контуре постоянную силу тока I =50 А, его переместили из поля в область пространства, где поле отсутствует. Определить магнитную индукцию В поля, если при перемещении контура была совершена работа А=0,4 Дж.
293. Определить магнитный поток Ф, пронизывающий соленоид, если его длина l=50 см и магнитный момент pm=0,4 А.м2.
294. В однородном магнитном поле В=0,1 Тл равномерно с частотой ν=5 с-1 вращается стержень длиной l=50 см так, что плоскость его вращения перпендикулярна линиям напряженности, а ось вращения проходит через один из его концов. Определить индуцируемую на концах стержня разность потенциалов U.
295. В однородном магнитном поле В=0,5 Тл равномерно с частотой ν=10 с-1 вращается стержень длиной l=20 см. Ось вращения параллельна линиям индукции и проходит через один из концов стержня. Определить разность потенциалов U на концах стержня.
296. Тонкий медный провод массой m=5 г согнут в виде квадрата; концы его замкнуты. Квадрат помещён в однородное магнитное поле В=0,2 Тл так, что его плоскость перпендикулярна линиям поля. Определить заряд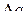 
, который протечёт по проводнику, если квадрат, потянув за противоположные вершины, вытянуть в линию.
297. Рамка из провода сопротивлением R=0,04 Ом равномерно вращается в однородном магнитном поле В=0,6 Тл. Ось вращения лежит в плоскости рамки и перпендикулярна линиям индукции. Площадь рамки S=200 см2. Определить заряд 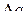, который протечёт по рамке при изменении угла между нормалью к рамке и линиями индукции: 1) от 0° до 45°; 2) от 45° до 90°.
298. Проволочный виток диаметром D=5 см и сопротивлением R=0,02 Ом находится в однородном магнитном поле В=0,3 Тл. Плоскость витка составляет угол φ=40° с линиями индукции. Какой заряд 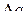протечёт по витку при выключении магнитного поля?
299. Рамка, содержащая N=200 витков тонкого провода, может вращаться относительно оси, лежащей в плоскости рамки. Площадь рамки S=50 см2. Ось рамки перпендикулярна линиям индукции однородного магнитного поля В=0,05 Тл. Определить максимальную ЭДС ε max, которая индуцируется в рамке при её вращении с частотой ν=40 с-1.
300. Проволочный контур площадью S=500 см2 и сопротивлением R=0,1 Ом равномерно вращается в однородном магнитном поле В=0,5 Тл. Ось вращения лежит в плоскости кольца и перпендикулярна линиям магнитной индукции. Определить максимальную мощность Р max, необходимую для вращения контура с угловой скоростью ω=50 рад/с.
301. Кольцо из медного провода массой m=10 г помещено в однородное магнитное поле В=0,5 Тл так, что плоскость кольца составляет угол β=600 с линиями магнитной индукции. Определить заряд 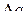, который пройдет по кольцу после снятия магнитного поля.
302. Соленоид сечением S=10 см2 содержит N=200 витков. При силе тока I=5 А магнитная индукция поля внутри соленоида равна 0,05 Тл. Определить индуктивность L соленоида.
303. Индуктивность соленоида, намотанного в один слой на немагнитный каркас, L=0,5 мГн. Длина соленоида l=0,6 м, диаметр D=2 см. Определить отношение числа витков к его длине.
304. Соленоид содержит N=800 витков. Сечение сердечника (из немагнитного материала) S=10 см2. По обмотке течет ток, создающий поле с индукцией В=0,8 мТл. Определить среднее значение ЭДС < ε s > самоиндукции, которая возникает на зажимах соленоида, если сила тока уменьшается практически до нуля за время Δt=0,8 мс.
305. По катушке индуктивностью L=8 мкГн течет ток I=6 А. Определить среднее значение ЭДС < ε s > самоиндукции, возникающей в контуре, если сила тока изменяется практически до нуля за время Δt=5 мс.
306. В электрической цепи, содержащей резистор сопротивлением R=20 Ом и катушку индуктивностью L=0,06 Гн, течёт ток I=20 А. Определить силу тока I в цепи через Δt=0,2 мс после того, как источник тока отключили, не разрывая цепи.
307. Цепь состоит из катушки индуктивностью L=0,1 Гн и источника тока. Источник тока отключили, не разрывая цепи. Время, за которое сила тока уменьшится до 0,001 первоначального значения, равно t=0,07 с. Определить сопротивление катушки.
308. Источник тока замкнули на катушку сопротивлением R=10 Ом и индуктивностью L=0,2 Гн. Через какое время сила тока в цепи достигнет 50% максимального значения?
309. Источник тока замкнули на катушку сопротивлением R=20 Ом. Через время t=0,1 с сила тока I в катушке достигла 0,95 предельного значения. Определить индуктивность L катушки.
310. Колебательный контур состоит из конденсатора ёмкостью С и катушки с индуктивностью L=38 мкГн и сопротивлением R=5,3 Ом. Добротность контура равна Q=110. Определить длину волны λ, на которую настроен контур.
311. Колебательный контур состоит из конденсатора ёмкостью С=68 пФ и катушки с индуктивностью L и сопротивлением R=1,2 Ом. Контур настроен на длину волны λ=27 м. Определить добротность контура Q.
312. Колебательный контур состоит из конденсатора ёмкостью С=810 пФ и катушки с индуктивностью L и сопротивлением R. Добротность контура равна Q=95. Контур настроен на длину волны λ=170 м. Определить сопротивление R .
313. Колебательный контур состоит из конденсатора ёмкостью С=0,5 нФ и катушки индуктивностью L=0,4 мГн. Определить длину волны излучения, генерируемого контуром.
314. Определить длину электромагнитной волны в вакууме, на которую настроен колебательный контур, если максимальный заряд на обкладках конденсатора Q=50 нКл, а максимальная сила тока в контуре I=1,5 А. Активным сопротивлением контура пренебречь.
315. На какой диапазон волн можно настроить колебательный контур, если его индуктивность равна 2∙10-3 Гн, а ёмкость может меняться от 69 до 533 пФ? Сопротивление контура ничтожно мало.
316. Колебательный контур имеет индуктивность L=1,6 мГн, ёмкость С=0,04 мкФ. Максимальное напряжение на зажимах конденсатора U=200 В. Чему равна максимальная сила тока в контуре? Сопротивление контура ничтожно мало.
317. Колебательный контур состоит из параллельно соединённых конденсатора ёмкостью С=1 мкФ и катушки индуктивности L=1 мГн. Сопротивление контура ничтожно мало. Найти частоту колебаний ν.
318. Индуктивность колебательного контура L=0,5 мГн. Какова должна быть ёмкость контура, чтобы он резонировал на длину волны λ=300 м?
319. Колебательный контур имеет индуктивность L=0,5 мГн и ёмкость С=8 пФ. Максимальное значение силы тока равно Imax=40 мА. Каково максимальное напряжение на обкладках конденсатора?
320. На какую длину волны будет резонировать контур, состоящий из катушки индуктивностью L=4 мкГн и конденсатора ёмкостью С=1,11 нФ?
Дата: 2019-02-25, просмотров: 278.
