МОЛЕКУЛЯРНАЯ ФИЗИКА. ОСНОВЫ ТЕРМОДИНАМИКИ

Гидродинамика

· Объёмный 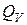 и массовый  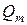расход жидкости или газа:

;

.

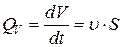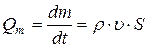Здесь 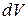 – объём (  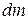– масса) газа или жидкости плотностью 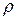, протекающий со скоростью  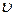за время  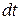через сечение площадью  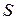трубки тока.

· Уравнение неразрывности струи для несжимаемой жидкости или газа:

,

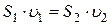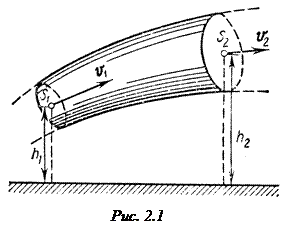
где S₁ и S₂ – площади поперечного сечения трубки тока в двух местах; υ₁ и υ₂  – соответствующие скорости течений (рис. 2.1).

· Уравнение Бернулли для идеальной (без вязкости) несжимаемой идеальной жидкости или газа:

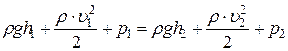, или ,

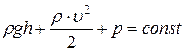где 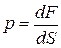 – статическое давление,  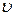– скорость течения,  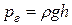– гидростатическое давление; h – высота сечения над некоторым уровнем,  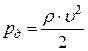– динамическое давление. Индексы «1» и «2» относятся к двум любым сечениям трубки тока для стационарного течения (рис. 2.1).

· Скорость истечения жидкости из малого отверстия в открытом широком сосуде:

,

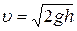где h – глубина, на которой находится отверстие относительно уровня жидкости в сосуде.

· Закон Архимеда: на тело, погружённое в жидкость или газ, действует выталкивающая сила 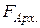, равная весу вытесненной жидкости (газа):

,

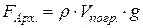где 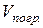 – объём погружённой в жидкость части тела,  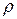– плотность жидкости (газа).

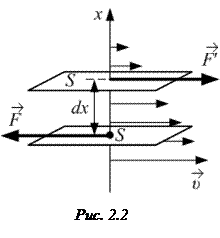· Формула Ньютона для вязкой жидкости (газа). Сила F вязкого трения, действующая между двумя слоями стационарно текущего газа или жидкости, прямо пропорциональна площади S слоёв и градиенту скорости  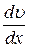направленного движения слоёв (рис. 2.2):

,

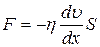где η – коэффициент динамической вязкости. Знак «минус» показывает, что сила вязкости тормозит слой жидкости, движущийся быстрее.

· Формула Пуазейля. Объёмный расход жидкости (газа), протекающей через трубку (капилляр) длиной l и радиусом R, на концах которой создана разность давлений :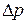

,

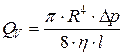где η – динамическая вязкость (коэффициент внутреннего трения) жидкости (газа).

· Кинематическая вязкость:

,

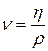где 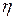 – динамическая вязкость,  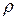– плотность жидкости (газа).

· Число Рейнольдса для потока жидкости (газа) в длинных трубках:

,

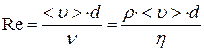где 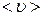 – средняя по сечению трубки скорость течения жидкости; d – диаметр трубки,  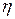– динамическая вязкость,  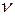– кинематическая вязкость,  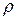– плотность жидкости (газа).

· Число Рейнольдса для шарика диаметром d, движущегося в вязкой жидкости или газе со скоростью :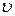

.

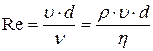Число Рейнольдса 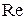 есть функция скорости  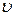тела, линейной величины d, определяющей размеры тела, плотности  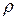и динамической вязкости η жидкости, то есть 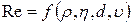. При малых значениях чисел Рейнольдса, меньших некоторого критического значения 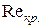, движение жидкости является ламинарным (слоистым, без перемешивания). При значениях  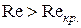движение жидкости переходит в турбулентное (вихревое). Критическое число Рейнольдса для движения шарика в жидкости 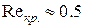; для потока жидкости в длинных трубках .

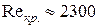· Формула Стокса. Сила сопротивления F, действующая со стороны вязкой жидкости (или газа) на движущийся в ней со скоростью 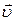 шарик радиусом r:

,

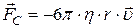где 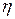 – динамическая вязкость среды. Формула справедлива при ламинарном обтекании шарика.