Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

· Спин 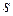 – внутреннее характерное неотъемлемое свойство элементарных частиц (наряду с массой и зарядом). Спин электрона и фотона:

;   .

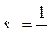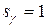Спин определяет собственный (спиновый) механический момент импульса частицы 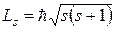 и связанный с ним магнитный момент 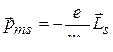. Здесь  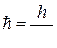– постоянная Планка с чертой, е – модуль заряда электрона, m_e – его масса. Спин – квантовый релятивистский эффект. Классического аналога для спина нет. Частицы подчиняются разным статистическим закономерностям, в зависимости от того, целый спин у частиц или полуцелый.

· Функция распределения Бозе-Эйнштейна (квантовая статистика для бозонов – частиц с целым спином; пример - фотоны):

, ,

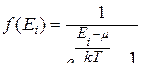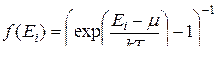где i – номер квантового состояния; 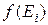 – средняя заселённость i-го состояния ( 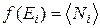;  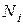– число частиц в i-м состоянии);  – энергия частицы в i-том состоянии; k – постоянная Больцмана; T – температура; 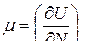 – химический потенциал (увеличение внутренней энергии системы при добавлении в неё одной частицы при постоянных объёме и энтропи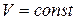и:  и ).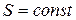

· Функция распределения Ферми-Дирака (квантовая статистика для фермионов – частиц с полуцелым спином; пример – электроны):

, ,

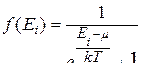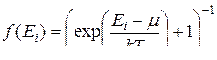где i – номер квантового состояния; 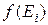 – средняя заселённость i-го состояния ( 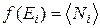;  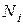– заселённость, то есть число частиц в i-м состоянии; для фермионов может быть только 0 или 1);  – энергия частицы в i-том состоянии; 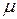 – химический потенциал, в первом приближении для фермионов равный энергии Ферми ( 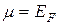); k – постоянная Больцмана; T – температура. Для фермионов  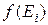имеет также смысл вероятности заполнения i-го состояния.

· Энергия Ферми – это максимальная энергия электронов при 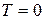; она зависит от концентрации электронов n: чем больше частиц, тем большее число уровней будет занято и тем выше окажется последний занятый уровень (рис. 6.4), и тем выше соответствующая энергии  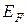температура Ферми :

; .

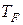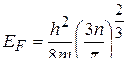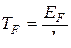Положение уровня Ферми немного зависит от температуры, поэтому при температурах T>0 уровнем Ферми по определению называется уровень, вероятность заполнения которого равна 0.5:

.

 

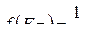Температурная зависимость сопротивления металлов и полупроводников. p - n – переход. Термоэлектричество

· Зависимость сопротивления R и удельного сопротивления ρ металла от температуры

,

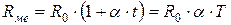где 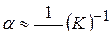 – температурный коэффициент сопротивления (удельного сопротивления) для чистых металлов;  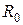( 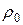) – сопротивление (удельное сопротивление) при 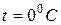,  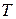– абсолютная температура.

· Зависимость сопротивления R , удельного сопротивления ρ и проводимости γ собственного полупроводника от температуры:

,

,

,

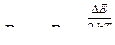где k – постоянная Больцмана; T – абсолютная температура; ΔE – ширина запрещённой зоны, то есть минимальная энергия, необходимая для переходя электрона из валентной зоны в зону проводимости и образования пары электрон-дырка в беспримесном полупроводнике (рис. 6.5).

· Сила тока, текущего через p - n – переход:

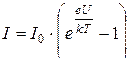, или .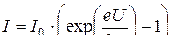

Здесь 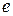– элементарный заряд, k – постоянная Больцмана, T – абсолютная температура, U – напряжение на p - n – переходе (U>0 для прямого включения и U<0 – для обратного).

· Термоэлектродвижущая сила (ТЭДС), возникающая в замкнутой цепи, составленной из разнородных проводников с различными температурами спаев (контактов):

,

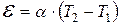где (T₂–T₁) – разность температур спаев термопары; 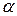 – удельная термо-ЭДС.

Строение ядра

· Дефект массы ядра:

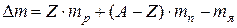, или ,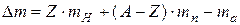

где 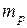 – масса протона,  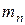– масса нейтрона,  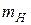– масса атома водорода 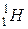,  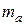и 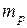 – масса атома и его ядра 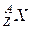, Z – зарядовое число ядра (число протонов в ядре), A – массовое число (суммарное число нуклонов – протонов и нейтронов – в ядре).

· Энергия связи ядра

,

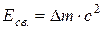где 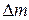 – дефект массы ядра, с – скорость света в вакууме. Если дефект массы выражен в атомных единицах массы (а.е.м.), то 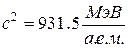; иначе говоря, 1 а.е.м. эквивалентна энергии 931.5 МэВ.

· Удельная энергия связи – это энергия связи, приходящаяся на один нуклон:

.

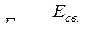где А – массовое число.

· Закон радиоактивного распада:

,

где 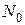 – начальное число радиоактивных ядер в момент времени t=0; N – число ядер, оставшихся нераспавшимися в момент времени t; λ – постоянная радиоактивного распада (вероятность распада ядра в единицу времени).

· Период полураспада – это время, за которое распадается половина ядер; оно связано с постоянной радиоактивного распада:

.

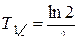· Активность радиоактивного вещества – это число распадов в единицу времени:

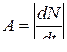 , или ,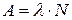

где λ – постоянная распада, N – число радиоактивных ядер в момент времени t.

· Энергетический эффект ядерной реакции :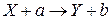

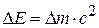 (система единиц СИ: 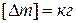, 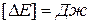),  или

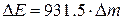 (атомные единицы: , ),

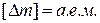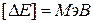где 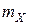, , 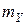 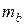и 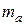 – массы ядер или частиц, участвующих в реакции;  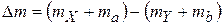– изменение массы при ядерной реакции.

 

Задачи к разделу 6

401. В баллоне, объём которого 0,25 м³ находится газ, состоящий из смеси углекислого газа и паров воды. Температура газа 327 ^°С. Число молекул углекислого газа N ₁=6,6∙10²¹, число молекул паров воды N ₂=0,9∙10²¹. Вычислить давление р и среднюю молярную массу μ газовой смеси.

402. Плотность газа, состоящего из смеси гелия и аргона при давлении 1,5 атм и температуре 27 ^°С, равна ρ=2 г/л. Сколько атомов гелия содержится в 1 см³ газовой смеси?

403. Определить среднюю кинетическую энергию <Е_пост> поступательного движения и среднее значение <Е_кин> полной кинетической энергии молекулы водяного пара при температуре Т=600 К. Найти кинетическую энергию U _пост поступательного движения всех молекул пара, содержащего количество вещества ν=1 кмоль.

404. Найти энергию U теплового движения молекул NH₃, находящихся в баллоне объёмом 10 л, при давлении 18,4 мм рт.ст. Какую часть этой энергии составляет энергия поступательного движения молекул U _пост? Молекулы считать жесткими.

405. Теплоизолированный сосуд с азотом движется со скоростью υ=86 м/с. Температура газа 0 ^°С. Какова будет средняя энергия поступательного движения молекул газа <Е_пост>, если сосуд остановить?

406. В баллоне, объём которого 2,55 л, находится m=1,5∙10^{-2 г} водорода при температуре 2500^°С. При этой температуре молекулы водорода оказываются упругими, причем часть молекул диссоциирует на атомы. Степень диссоциации молекул α=0,25. Вычислить давление р и количество теплоты ΔQ, необходимое для нагревания водорода на 1^°С при указанных условиях.

407. Какое число молекул аммиака занимают объём 50 мл при давлении 0.1 атм и температуре 300 К? Какой энергией теплового движения обладают эти молекулы?

408. Определить суммарную кинетическую энергию поступательного движения всех молекул газа, находящегося в сосуде объёмом 3 л под давлением 540 кПа.

409. Определить среднюю кинетическую энергию поступательного движения молекул газа, находящегося под давлением 0,1 Па. Концентрация молекул газа равна 10¹³ см³.

410. В баллоне вместимостью V=1 л находится азот при нормальных условиях. Когда азот нагрели до температуры Т=1,8 кК, то молекулы азота оказались частично диссоциированными на атомы. Степень диссоциации α=0,3. Определить количество вещества ν и концентрацию n атомов атомарного азота после нагревания.

411. Найти отношение средней квадратичной скорости молекул газа к скорости распространения звука в идеальном газе при той же температуре. Газ состоит из одноатомных молекул.

412. При какой температуре Т₂ молекулы кислорода имеют такую же среднюю квадратичную скорость, как молекулы водорода при температуре Т₁=100 К?

413. Средняя квадратичная скорость некоторого газа при нормальных условиях равна 480 м/с. Сколько молекул содержит один грамм этого газа?

414. Определить скорость υ_вер, соответствующую максимуму функции распределения при t=100 ^°С для водорода, гелия и азота.

415. Какая часть молекул кислорода при температуре 17°С обладает скоростями, отличающимися не больше чем на 0.50 м/с от скорости, равной υ_вер?

416. Азот находится при температуре 0°С. Чему равна доля молекул, скорость которых отличаются от средней квадратичной не более, чем на 2%?

417. При каком значении скорости υ пересекаются кривые распределения Максвелла для температур Т₁ и Т₂=2∙Т₁? Ответ представьте как долю вероятной скорости υ_вер2 при температуре Т₂: υ = η υ_вер2.

418. При какой температуре средняя квадратичная скорость молекул кислорода больше их наиболее вероятной скорости на 100 м/с?

419. Какая часть молекул водорода при температуре 500°С обладает скоростями в пределах 420÷430 м/с?

420. Найти число молекул гелия в 1 см³, скорости которых лежат в интервале от 2.59^.10³ м/с до 2.61^.10³ м/с. Температура гелия 690°С, его плотность 2.16^.10^-4 кг/м³.

421. Найти давление воздуха в шахте на глубине 10 км. На поверхности земли давление 760 мм рт. ст., относительный молекулярный вес воздуха равен 29. Считать, что температура воздуха не зависит от высоты и равна 0 ^°С.

422. Предположим, что внутри вертикальной трубы высотой 100 м находится воздух при температуре 500 К; снаружи труба окружена воздухом при температуре 250 К. Труба сверху открыта, а внизу отделена от наружного воздуха заслонкой площадью 300 см². Какая сила действует на заслонку, если давление воздуха у верхнего конца трубы равно 740 мм рт.ст.? Относительный молекулярный вес воздуха равен 29.

423. Вычислить массу азота и массу кислорода в 1 м³ воздуха на уровне моря и на вершине Эльбруса (высота 5642 м). На уровне моря давление воздуха равно 1,01∙10⁵ Н/м²; массовая доля кислорода – 23%, азота – 77%; остальными примесями пренебречь. Средняя молярная масса воздуха равна 29 г/моль. Температура воздуха одинакова по высоте и равна 0^°С.

424. На какой высоте h над уровнем моря плотность воздуха уменьшается в два раза? Считать, что температура воздуха t=0 ^°С и ускорение g не зависят не зависят от h. Относительный молекулярный вес воздуха равен 29.

425. На какой высоте h над уровнем моря плотность кислорода уменьшается на 1%? Температура кислорода t=27 ^°С.

426. На какой высоте давление воздуха составляет 60% от давления на уровне моря? Считать, что температура воздуха везде одинакова и равна 10 ^°С. Относительный молекулярный вес воздуха равен 29.

427. Пылинки, взвешенные в воздухе, имеют массу m=10^{-18 г}. Во сколько раз уменьшится их концентрация n при увеличении высоты на Δh=10 м? Температура воздуха Т=300 К.

428. Насколько уменьшится атмосферное давление р=100 кПа при подъёме наблюдателя над поверхностью Земли на высоту h=100 м? Считать, что температура воздуха Т=290 К и не изменяется с высотой. Относительный молекулярный вес воздуха равен 29.

429. Найти изменение высоты Δh, соответствующее изменению давления на Δр=100 Па вблизи поверхности Земли, где температура Т=290 К, давление р=100 кПа. Относительный молекулярный вес воздуха равен 29.

430. Барометр в кабине летящего самолета все время показывает одинаковое давление р=80 кПа, благодаря чему лётчик считает высоту h полета неизменной. Однако температура воздуха изменилась на ΔТ=1 К. Какую ошибку Δh в определении высоты допустил лётчик? Считать, что температура не зависит от высоты и что у поверхности Земли давление р₀=100 кПа. Относительный молекулярный вес воздуха равен 29.

431. Определить среднюю длину свободного пробега < l > молекул газа, находящегося при температуре t=17^°С и давлении р=360 мм рт. ст. Эффективный диаметр молекул d=0,29 нм.

432. Средняя длина свободного пробега атомов гелия при нормальных условиях < l >=180 нм. Определить коэффициент диффузии D гелия.

433. Вычислить динамическую вязкость кислорода при нормальных условиях. Эффективный диаметр молекул кислорода считать равным 0,35 нм.

434. Определить коэффициент теплопроводности азота при температуре Т=280 К. Эффективный диаметр молекул азота принять равным 0,37 нм.

435. Азот находится под давлением р=100 кПа при температуре Т=290 К. Определить коэффициенты диффузии D и внутреннего трения η. Эффективный диаметр молекул азота принять равным 0,37 нм.

436. Пространство между двумя параллельными пластинами площадью S=150 см² каждая, находящимися на расстоянии 5 мм друг от друга, заполнено кислородом. Одна пластина поддерживается при температуре –17 ^°С, другая – при температуре 27^°С. Определить количество теплоты, прошедшее за 5 минут посредством теплопроводности от одной пластины к другой. Кислород находится при нормальных условиях. Эффективный диаметр молекул кислорода считать равным 0,35 нм.

437. Толщина деревянной стены равна 12 см. Какой должна быть толщина кирпичной стены, чтобы она обладала такой же теплопроводностью, как деревянная? Коэффициент теплопроводности дерева равен 0.17 Вт/(м^.К), а кирпича 0.69 Вт/(м^.К).

438. Какое количество теплоты проходит за 1 с через медный стержень с площадью поперечного сечения 10 см² длиной 50 см, если разность температур на концах стержня 15 К? Тепловыми потерями через стенки пренебречь. Коэффициент теплопроводности меди 380 Дж/(м^.с^.К).

439. Найти количество азота, прошедшего через площадку 100 см² за 10 с, если градиент плотности равен 1.26 кг/м⁴. Температура азота 27⁰С, средняя длина свободного пробега 0.1 мкм.

440. Температура в комнате 293 К, снаружи 253 К. Размеры стены комнаты, выходящей на улицу, 2.7х5 м², толщина стены 0.5 м. Какое количество теплоты теряется за 1 с, если коэффициент теплопроводности кирпича 0.7 Вт/(м^.К)? Потерями теплоты через внутренние стены, пол и потолок пренебречь.

441. Концы железной балки сечением 75 см² упираются в две стены. Температура 0⁰С. Определить силу, которая будет действовать на стены, если температура повысится на 20 К.

442. a-железо имеет кубическую объёмно-центрированную структуру (а=2.86 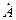), g-железо – кубическую структуру с центрированными гранями (а=3.56 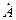). Как изменится плотность железа при переходе его из a- в g-модификацию?

443. При каком растягивающем напряжении медный стержень получит такое же удлинение, как и при нагревании от 0⁰С до 100⁰С?

444. На нагревание медной болванки массой 1 кг, находящейся при температуре 0⁰С, затрачено 138 кДж. Во сколько раз при этом увеличился её объём? Теплоёмкость меди найти по закону Дюлонга и Пти. Относительная атомная масса меди равна 63.5.

445. Вычислить по классической теории теплоёмкости удельные теплоёмкости кристаллов: алюминия, меди, платины. Относительные атомные массы алюминия, меди, платины 27, 63.5 и 195 соответственно.

446. Вычислить по классической теории теплоемкости удельные теплоемкости кристаллов KCl и CaCl₂. Относительные атомные массы калия, хлора и кальция 39, 35.5 и 40 соответственно.

447. Алюминиевый диск, взятый при температуре 0⁰С, при нагревании увеличил свой объём на 4.6 см³. Какое количество теплоты затрачено на нагревание?

448. Пользуясь классической теорией теплоемкости, найти, во сколько раз удельная теплоемкость алюминия больше удельной теплоемкости платины. Относительные атомные массы алюминия и платины 27 и 195 соответственно.

449. Алюминий имеет гранецентрированную кубическую решетку. Параметр решётки а=0,404 нм. Определить плотность алюминия.

450. Плотность кристалла ρ=534 кг/м³. Определить относительную атомную массу А, если расстояние между ближайшими соседними атомами d=0,304 нм. Решётка объёмно-центрированная кубическая.

451. Как и во сколько раз изменится вероятность заполнения электронами энергетического уровня в металле, если уровень расположен на 0.01 эВ ниже уровня Ферми и температура изменяется от 200 до 300 К?

452. Определить вероятность того, что электрон в металле займет энергетическое состояние, лежащее ниже уровня Ферми на DЕ=0.05 эВ и выше уровня Ферми на DЕ=0.05 эВ в двух случаях: а) температура металла Т=290К; б) температура металла Т=58 К.

453. На какой высоте (в электрон-вольтах) от дна зоны проводимости находится уровень Ферми в одновалентном натрии, который содержит 2.5^.10²³ атомов/м³? Считать температуру равной 0 К.

454. Какова вероятность заполнения электронами в металле энергетического уровня, расположенного на 0.001 эВ ниже уровня Ферми, при температуре 18°С?

455. При какой температуре вероятность найти в проводнике электрон с энергией 0.5 эВ над уровнем Ферми равна 2%?

456. Найти разницу энергий (в единицах kT) между электро­ном, находящимся на уровне Ферми, и электронами, находящимися на уровнях, вероятности заполнения которых равны 0.20 и 0.80.

457. Полагая, что на каждый атом алюминия в кристалле приходится по три свободных электрона, найти максимальную энергию электронов при 0 К.

458. Определить максимальную скорость электронов в металле при температуре Т=0 К, если уровень Ферми Е _F=5 эВ.

459. Определить концентрацию n свободных электронов при температуре Т=0 К. Энергию Ферми принять Е _F=1 эВ.

460. Определить отношение концентраций 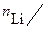 свободных электронов при Т=0 К в литии и цезии, если известно, что уровни Ферми в этих металлах соответственно равны 4,72 эВ и 1,53 эВ.

461. Германиевый кристалл, ширина запрещенной зоны в котором равна 0.72 эВ, нагревают от температуры 0⁰С до температуры 15⁰С. Во сколько раз возрастёт его удельная электропроводимость?

462. При нагревании кремниевого кристалла от температуры 0⁰С до температуры 10⁰С его удельная электропроводимость возрастает в 2.28 раза. Определить ширину запрещённой зоны кремния.

463. Во сколько раз изменится при повышении температуры от 300 до 310 К проводимость: а) металла; б) собственного полупроводника, ширина запрещенной зоны которого 0.3 эВ?

464. Во сколько раз уменьшится сопротивление полупроводника при увеличении абсолютной температуры на 10%, если его начальная температура 27⁰С, а ширина запрещенной зоны 0.6 эВ?

465. Найти минимальную энергию образования пары электрон-дырка в беспримесном полупроводнике, проводимость которого возрастает в 5 раз при увеличении температуры от 300 K до 400 К.

466. p - n –переход находится под обратным напряжением 0.1 В. Его сопротивление 1 кОм. Каково сопротивление p - n –перехода при таком же прямом напряжении? Т=293 К.

467. Прямое напряжение, приложенное к p - n –переходу, равно 2 В. Во сколько раз возрастёт сила тока через переход, если изменить температуру от 300 К до 273 К?

468. Термопара висмут-железо с постоянной 92 мкВ/К и сопротивлением 5 Ом присоединена к гальванометру с внутренним сопротивлением 100 Ом. Какую силу тока покажет гальванометр, если температура одного спая термопары 100⁰С, а другого 0⁰С?

469. Сила тока в цепи, состоящей из термопары сопротивлением 4 Ом и гальванометра сопротивлением 80 Ом, равна 26 мкА при разности температур спаев 50 К. Определить постоянную термопары.

470. Сопротивление p - n –перехода, находящегося под прямым напряжением 0.2 В, равно 10 Ом. Определить сопротивление p - n –перехода при таком же обратном напряжении. Т=293 К.

471. Определить энергию ядерной реакции ⁶₃Li + ²₁H → ⁴₂He + ⁴₂He. Освобождается или поглощается энергия?

472. Определить энергию ядерной реакции ⁷₃Li+ ⁴₂He→ ¹⁰₅B+ ¹₀n. Освобождается или поглощается энергия?

473. Какую минимальную энергию нужно затратить, чтобы оторвать один нейтрон от ядра азота ¹⁴₇N?

474. Определить энергию E, которая выделится при образовании из протонов и нейтронов ядер гелия ⁴₂He массой m=1 г.

475. Энергия связи E_св ядра, состоящего из двух протонов и одного нейтрона, равна 7,71 МэВ. Определить массу m_а нейтрального атома, имеющего это ядро.

476. Определить удельную энергию связи E_уд ядра ¹²₆C.

477. Определить дефект массы Δm и энергию связи E_св ядра атома тяжелого водорода.

478. Определить промежуток времени τ, в течение которого активность А изотопа стронция Sr⁹⁰ уменьшится в к₁=10 раз; в к₂=100 раз.

479. Найти электрическую мощность P атомной электростанции, расходующей 0,1 кг урана-235 в сутки, если КПД η станции равен 16 %. При распаде одного ядра ²³⁵U выделяется энергия, приблизительно равная ΔЕ₁≈200 МэВ.

480. За время t=8 суток распалось к=¾ начального количества ядер радиоактивного изотопа. Определить период полураспада.

 

ПРИЛОЖЕНИЯ

Таблица 3