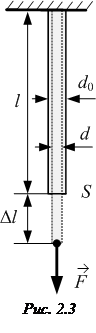
· Относительная продольная деформация при продольном растяжении (или сжатии) тела:
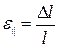 ,
,
где 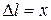 – абсолютное удлинение, l – начальная длина тела (рис. 2.3).
– абсолютное удлинение, l – начальная длина тела (рис. 2.3).
· Относительное поперечное сжатие при продольной деформации (рис.2.3):
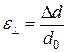 ,
,
где 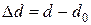 – изменение диаметра стержня при деформации.
– изменение диаметра стержня при деформации.
· Коэффициент Пуассона материала:
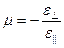 ,
,
где 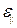 – относительная продольная деформация;
– относительная продольная деформация; 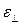 – относительное поперечное сжатие.
– относительное поперечное сжатие.
 · Нормальное механическое напряжение:
· Нормальное механическое напряжение:
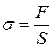 ,
,
где F – сила, перпендикулярная поперечному сечению тела площадью S (рис. 2.3).
· Закон Гука для деформации сжатия-растяжения:
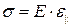 , или
, или 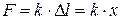 .
.
Здесь 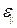 – относительное удлинение, E – модуль Юнга материала, k – жёсткость (коэффициент жёсткости), равный для стержня величине
– относительное удлинение, E – модуль Юнга материала, k – жёсткость (коэффициент жёсткости), равный для стержня величине 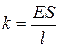 .
.
· Тангенциальное механическое напряжение
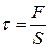 ,
,
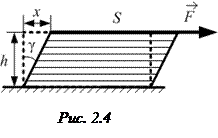 где F – касательная сила, действующая вдоль слоя тела площадью S (рис. 2.4).
где F – касательная сила, действующая вдоль слоя тела площадью S (рис. 2.4).
· Относительная деформация при сдвиге (относительный сдвиг) для малых деформаций (рис. 2.4):
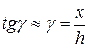 .
.
Здесь x – абсолютный сдвиг параллельных слоев тела относительно друг друга; h – расстояние между слоями.
· Закон Гука для деформации сдвига:
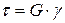 ,
,
где G – модуль модуль сдвига.
· Связь между модулем Юнга E и модулем сдвига G:
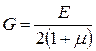 ,
,
где 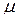 – коэффициент Пуассона материала.
– коэффициент Пуассона материала.
· Закон Гука для деформации кручения:
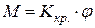 ,
,
где М – момент силы, закручивающий однородный круглый стержень на угол φ; 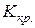 – постоянная кручения.
– постоянная кручения.
· Потенциальная энергия растянутого или сжатого стержня
- при однородной деформации:
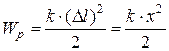 ;
;
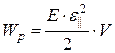
- при неоднородной деформации:
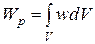 ,
,
где 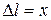 – абсолютное удлинение; k – жёсткость; Е – модуль Юнга;
– абсолютное удлинение; k – жёсткость; Е – модуль Юнга; 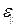 – относительная продольная деформация; V – объём тела; w – объёмная плотность энергии, равная, по определению, энергии, приходящейся на единичный объём:
– относительная продольная деформация; V – объём тела; w – объёмная плотность энергии, равная, по определению, энергии, приходящейся на единичный объём: 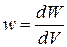 .
.
· Объёмная плотность энергии упругой деформации
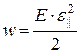 ,
,
где Е – модуль Юнга; 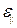 – относительная продольная деформация.
– относительная продольная деформация.
Молекулярная физика
· Относительная атомная масса элемента (они приводятся в таблице Д. И. Менделеева) – это масса 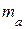 атома данного элемента, отнесённая к
атома данного элемента, отнесённая к 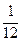 массы
массы 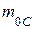 атома изотопа углерода
атома изотопа углерода 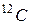 :
:
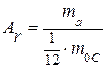
· Относительная молекулярная масса вещества – это масса 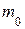 молекулы данного вещества, отнесённая к
молекулы данного вещества, отнесённая к 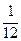 массы
массы 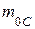 атома изотопа углерода
атома изотопа углерода 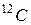 :
:
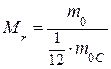 , или
, или 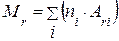
где 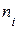 – число атомов i-го химического элемента, входящего в состав молекулы данного вещества;
– число атомов i-го химического элемента, входящего в состав молекулы данного вещества; 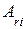 – относительная атомная масса этого элемента.
– относительная атомная масса этого элемента.
· Количество вещества определяется числом структурных элементов (молекул, атомов, ионов и т. п.), содержащихся в системе или теле. Количество вещества выражается в молях ( 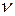 ). По закону Авогадро, один моль вещества содержит столько же структурных элементов, сколько содержится атомов в 12 граммах изотопа углерода
). По закону Авогадро, один моль вещества содержит столько же структурных элементов, сколько содержится атомов в 12 граммах изотопа углерода 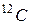 . Один моль вещества содержит число структурных элементов N, равное числу Авогадро
. Один моль вещества содержит число структурных элементов N, равное числу Авогадро 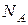 . Количество вещества равно
. Количество вещества равно
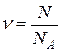 , или
, или 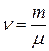 ,
,
где m – масса тела (системы); 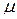 – молярная масса (масса моля вещества).
– молярная масса (масса моля вещества).
· Молярная масса вещества (масса моля):
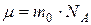 , или
, или 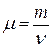 ,
,
где 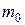 – масса одной молекулы;
– масса одной молекулы; 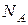 – число Авогадро, m – масса вещества,
– число Авогадро, m – масса вещества, 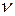 – количество вещества.
– количество вещества.
· Связь молярной массы 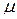 с относительной молекулярной массой
с относительной молекулярной массой 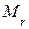 :
:
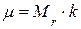 ,
,
где 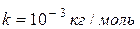 .
.
· Масса m вещества равна связана с числом молекул N:
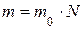 ,
,
где 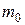 – масса одной молекулы.
– масса одной молекулы.
· Массовая доля смеси газов:
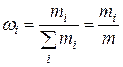 ,
,
где 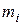 – масса i-го компонента смеси,
– масса i-го компонента смеси, 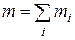 – масса всей смеси.
– масса всей смеси.
· Средняя молярная масса смеси газов:
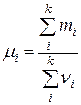 ,
,
где 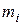 – масса,
– масса, 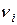 – количество вещества i-го компонента смеси; k – число компонентов смеси.
– количество вещества i-го компонента смеси; k – число компонентов смеси.
· Уравнение состояния идеального газа (уравнение Менделеева-Клапейрона) связывает параметры газа – давление p, объём 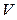 и термодинамическую температуру
и термодинамическую температуру 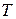 :
:
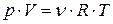 , или
, или 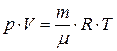 , или
, или 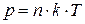 ,
,
где m – масса газа; 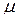 – его молярная масса;
– его молярная масса; 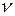 – количество вещества;
– количество вещества; 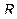 – универсальная газовая постоянная,
– универсальная газовая постоянная, 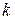 – постоянная Больцмана,
– постоянная Больцмана, 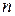 – концентрация молекул газа.
– концентрация молекул газа.
· Универсальная газовая постоянная 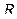 связана с постоянной Больцмана (
связана с постоянной Больцмана ( 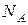 – число Авогадро):
– число Авогадро):
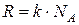 .
.
· Концентрация частиц (молекул, атомов и т. п.) однородной системы – это число частиц в единице объёма:
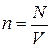 .
.
Здесь N – число частиц; V – объём.
· Закон Дальтона для смеси газов. Давление p смеси равно сумме парциальных давлений 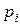 всех компонент смеси:
всех компонент смеси:
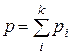 ,
,
где k – число компонент смеси.
Основы термодинамики
· П ервое начало термодинамики. Количество теплоты δQ, сообщённое системе, идёт на приращение её внутренней энергии и dU на работу δA системы против внешних сил:
δQ=dU+δA, или 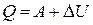 .
.
· Теплоёмкость тела:
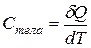 ,
,
где 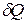 – количество теплоты, сообщённое телу,
– количество теплоты, сообщённое телу, 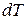 – соответствующее изменение температуры тела.
– соответствующее изменение температуры тела.
· Удельная теплоёмкость вещества – это теплоёмкость единицы массы:
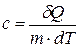 ,
,
где 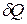 – количество теплоты;
– количество теплоты; 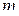 – масса вещества;
– масса вещества; 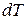 – соответствующее изменение его температуры.
– соответствующее изменение его температуры.
· Молярная теплоёмкость вещества – это теплоёмкость одного моля:
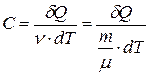 ,
,
где 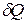 – количество теплоты;
– количество теплоты; 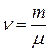 – количество вещества;
– количество вещества; 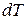 – соответствующее изменение его температуры.
– соответствующее изменение его температуры.
· Связь между молярной 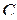 и удельной
и удельной 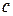 теплоёмкостями:
теплоёмкостями:
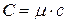 ,
,
где 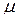 – молярная масса.
– молярная масса.
· Молярная теплоемкость идеального газа при постоянном объёме 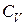 и при постоянном давлении
и при постоянном давлении 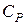 (по определению):
(по определению):
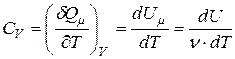 ;
; 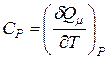 .
.
Здесь 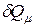 – теплота, сообщённая одному молю газа в соответствующем процессе;
– теплота, сообщённая одному молю газа в соответствующем процессе; 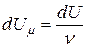 – изменение внутренней энергии одного моля газа;
– изменение внутренней энергии одного моля газа; 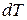 – изменение его температуры.
– изменение его температуры.
· Степени свободы; число степеней свободыi – это число независимых координат, однозначно определяющих положение тела (или молекулы) в пространстве. Для одноатомных молекулi =3, так как трёх координат (x, y, z) достаточно для того, чтобы однозначно задать положение материальной точки в трёхмерном пространстве. При температурах, не слишком низких и не слишком высоких, для двухатомных молекул i = 5; для многоатомных – i = 6 (с учётом вращательных степеней свободы).
· Показатель Пуассона (показатель адиабаты) – это отношение теплоёмкости 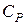 при постоянном давлении к теплоёмкости
при постоянном давлении к теплоёмкости 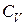 при постоянном объёме (здесь i – число степеней свободы молекул):
при постоянном объёме (здесь i – число степеней свободы молекул):
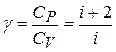 .
.
· Молярные теплоемкости идеального газа при постоянном объёме 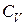 и постоянном давлении
и постоянном давлении 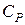 можно выразить через число степеней свободы молекулы i или через показатель Пуассона
можно выразить через число степеней свободы молекулы i или через показатель Пуассона 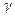 (
( 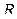 – универсальная газовая постоянная):
– универсальная газовая постоянная):
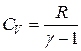 , или
, или 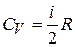 ;
;
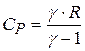 , или
, или 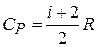 .
.
· Уравнение Майера
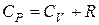 .
.
· Внутренняя энергия идеального газа
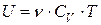 ,
,
где 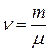 – количество вещества.
– количество вещества.
· Работа, связанная с изменением объёма газа, в общем случае:
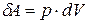 ;
; 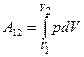 ,
,
где V1 – начальный объём газа; V2 – его конечный объём.
 · Термический коэффициент полезного действия (КПД) в общем случае:
· Термический коэффициент полезного действия (КПД) в общем случае:
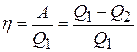 ,
,
где Q1 – количество теплоты, полученное рабочим телом (газом) от нагревателя; Q2 – количество теплоты, переданное рабочим телом охладителю, А – работа за цикл.
· КПД цикла Карно (рис. 2.5):
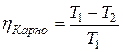 ,
,
где T1 – температура нагревателя; T2 – температура охладителя.
· Энтропия по определению Клаузиуса. Функция состояния системы, дифференциал 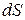 которой в обратимом процессе равен приведённой теплоте, является энтропией:
которой в обратимом процессе равен приведённой теплоте, является энтропией:
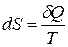 .
.
Здесь δQ – теплота, полученная системой; Т – её температура.
· Изменение энтропии в общем случае:
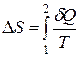 ,
,
где 1 и 2 – пределы интегрирования, соответствующие начальному и конечному состояниям системы. Так как процесс равновесный, то интегрирование проводится по любому пути.
· Изменение энтропии для процессов с идеальным газом (см. также табл. 3):
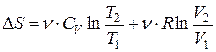 .
.
Таблица 2
Дата: 2019-02-25, просмотров: 310.