Определение числа станций на заданном участке трубопровода связано с балансом напоров насосных агрегатов станций и трубопровода, и при этом принято, что напоры и типы насосов всех станций одинаковы [7]:
Nэhп + nHст = (Z2 – Z1) + hпот + Nэhк , (5.13)
где Nэ – число эксплуатационных участков;
hп – напор подпорных агрегатов головной ЛПДС, м;
Hст – напор основных агрегатов одной ПС, м; Hст = m∙ Hосн
m – число работающих агрегатов одной ПС;
Hосн – напор основного агрегата, м;
Z1, Z2 – геодезические отметки начала и конца трубопровода, м;
hпот – потери напора в трубопроводе, определяются по уравнениям 5.7, 5.8, м;
hк – напор в конечной точке заданного участка трубопровода, м.
Эксплуатационный участок – это расстояние между станциями, имеющими в своем составе резервуарные парки, причем промежуточная ПС в этом случае должна быть конечным пунктом для предыдущего участка трубопровода и головной ПС для последующего.
Число станций из уравнения 5.13 равно
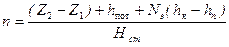 . (5.14)
. (5.14)
Получаемое по уравнению 5.14 расчетное число станций, как правило, дробное, его необходимо округлять до целого. Если округление произведено в меньшую сторону, то напор станции будет меньше напора трубопровода и фактическая производительность при меньшем числе станций будет снижаться по сравнению с принятой для расчета. При округлении в большую сторону зависимость противоположная, фактический напор станций и фактическая производительность будут превышать принятые для расчета. Сказанное выше хорошо иллюстрируется графиком на рис. 5.5 [2].
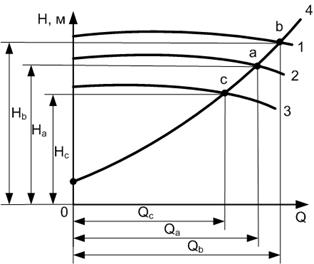
Рис. 5.5 Совмещенная характеристика насосных агрегатов и трубопровода при разном числе ПС
1 – напор, создаваемый всеми агрегатами станции, при округлении их числа в большую сторону;
2 – напор станций, если их число равно расчетному;
3 – напор станций при округлении их числа в меньшую сторону;
4 – характеристика трубопровода
По графику видно, что Hb > Ha > Hc и соответственно Qb > Qa > Qc. Однако в обоих случаях фактический напор и фактическую производительность можно оставить равными принятым к расчету, если при округлении в меньшую сторону использовать вставки большего диаметра, лупинги, или антитурбулентные присадки, при округлении в большую сторону применить агрегаты с меньшим напором за счет обточки рабочих колес или сменных роторов.
После уточнения числа станций, используя линии гидравлического уклона для каждого участка, можно на графике показать расстановку станций на заданном участке МТП (рис. 5.6). График строится в координатах H-L, горизонтальная ось соответствует длине трубопровода, по вертикальной оси откладываются геодезические отметки профиля трубопровода и напоры действующих на каждой ПС насосных агрегатов [7, 8].
Данное графическое построение удобно выполнить, используя масштабный треугольник АВС, у которого отношение сторон АВ/АС = tgα = iтр. При этом масштаб по оси L должен соответствовать катету АС, масштаб по оси Н – катету АВ треугольника АВС, линии гидравлического уклона А′А′′, В′В′′, К′К строятся параллельно гипотенузе ВС и тогда точки А, В, К соответствуют местам расположения перекачивающих станций ПС-2, ПС-3 и конечного пункта КП.
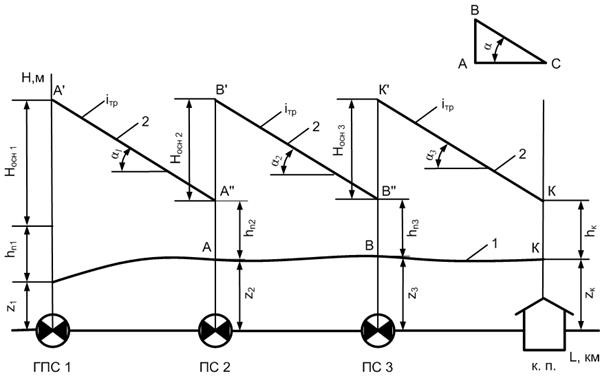
Рис. 5.6 – Графический метод расстановки станций на участке
магистрального трубопровода:
1 – профиль трубопровода; 2 - линии гидравлического уклона между станциями
Если принято решение использовать лупинг, то гидравлический уклон лупинга и производительность по лупингу определяются по уравнениям [8]:
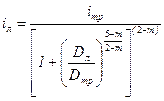 ; (5.15)
; (5.15)
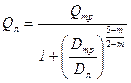 , (5.16)
, (5.16)
где
m – коэффициент, зависящий от режима движения потока в трубопроводе и равный [7]:
m = 1 - ламинарный режим;
m = 0,25 - зона гладких труб;
m = 0,123 - зона смешанного трения;
m = 0 - зона квадратичного трения.
Линия гидравлического уклона в этом случае строится с применением масштабного треугольника АВС, рис. 5.7, у которого отношение сторон
АВ/АС = tgα = iтр, а отношение сторон АВ'/АС = tgαл = iл.
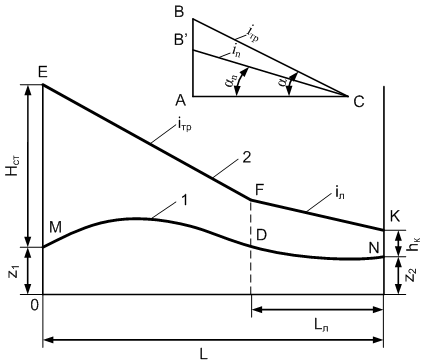
Рис. 5.7 – Линия гидравлического уклона для участка, имеющего лупинг:
∆ АВС – масштабный треугольник;
1 – профиль трубопровода;
2 – линия гидравлического уклона при наличии лупинга
При построении: линия EF || BC, FK || CB′, Lл – расчетная длина лупинга.
Общие потери напора на заданном участке трубопровода при производительности, принятой к расчету, и записываются в виде уравнения:
hпот = iтр(L – Lл) + iлLл (5.17)
Вместо лупингов возможно использование антитурбулентных присадок.
В середине двадцатого столетия английский ученый Томсон открыл эффект снижения гидравлических сопротивлений при введении в турбулентный поток жидкости высокомолекулярных присадок. Механизм действия таких присадок основан на гашении турбулентных пульсаций вблизи внутренней поверхности трубопровода за счет взаимодействия длинномерных молекул присадки с турбулентными вихрями, зарождающимися вблизи стенок трубопровода при чрезвычайно малых концентрациях присадки в потоке.
Так как введение присадки снижает коэффициент гидравлических сопротивлений, то с помощью эффекта Томсона можно изменить напор трубопровода при постоянной производительности, либо увеличивать производительность перекачки, не изменяя перепады давления на участке трубопровода. В зависимости от концентрации вводимой присадки эффект снижения величины "λ" может достигать 30 – 50 % от первоначального значения.
Ограничения в применении присадки – это: возможное изменение качества перекачиваемых нефтепродуктов и разрушение присадки при прохождении через насосные агрегаты.
В гидравлических расчетах величину "λ" определяют по универсальному закону сопротивления [9]:
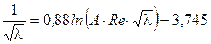 (5.18)
(5.18)
где А – коэффициент, зависящий от типа присадки и её концентрации в потоке, величина справочная [9].
Наиболее известные типы присадок – присадки "CDR-102" американской фирмы "Dupon-Conoco" и присадка "NECCAD-547" финской фирмы "Neste".
Расчет по данному уравнению величины коэффициента гидравлических сопротивлений ведется методом постепенных приближений, т.е. задаваясь величиной "λ", добиваются равенства обеих частей уравнения.
Задача №5
Дата: 2019-02-18, просмотров: 961.