Температура в любой точке трубопровода при перекачке нагретой нефти определяется на основе решения уравнений теплопередачи для б/м участков. Потери тепла по уравнению теплопередачи равны [3]

dq = KπD_Hdx(T-T₀), кДж/час,                                  (6.1)

где

dq – тепло, теряемое в окружающую среду через б/м поверхность πD_Hdx в единицу времени;

K – коэффициент теплопередачи от нефтепродукта к внешней среде, ;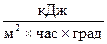

T-T₀– средний температурный напор или средняя движущая сила данного теплообменного процесса равна разности температур нефтепродукта t и окружающей среды t₀, ºК;

dx – длина участка, м.

Коэффициент теплопередачи К, входящий в данное уравнение, характеризует общий перенос тепла от потока к стенке трубопровода, через стенку и от стенки через грунт в окружающую среду, либо учитывают только теплоотдачу от стенки к грунту. Из курса термодинамики коэффициент К равен:

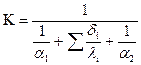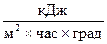, ,                             (6.2)

где

α₁, α₂ – частные коэффициенты теплоотдачи от потока к стенке и от стенки в окружающую среду или грунт, ;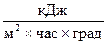

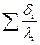 – сумма отношений толщины загрязнений стенки к коэффициенту теплопроводности загрязнений, толщины изоляции к коэффициенту теплопроводности изоляции, толщины стенки трубопровода к коэффициенту теплопроводности стенки.

α₁»α₂, поэтому часто принимают К ≈ α₂.

Обычно К ≈ 2 ÷ 3,5 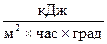 [10].

Непосредственно для нефти отдачу тепла можно представить уравнением

dq_H = - GcdТ, кДж/час,                                           (6.3)

где

G – массовый расход перекачки, кг/час;

c – средняя теплоемкость потока, кДж/кг×град;

dТ – разность температур потока и стенки трубопровода, ºК.

Для тепловых процессов, имеющих место в трубопроводе, dq = dq_н. Таким образом, можно записать уравнение:  

KπD_H(T – T₀) dx = – GcdT                                                    (6.4)

Знак минус говорит о потери тепла в данном тепловом процессе.

Разделив переменные, имеем уравнение

KπD_H dx = – GcdT/(T – T₀)                                                         (6.5)

Интегрирование данного уравнения в координатах 0 – Х и T_н – T приводит к уравнению В. П. Шухова (см. приложение А)

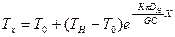,                                    (6.6)

где

T_х – текущая температура нефти по длине участка, ºК;

T₀ – температура окружающей среды, ºК;

T_н – начальная температура нефти, ºК;

е – основание натурального логарифма, равно 2,7.

Уравнение позволяет определить температуру продукта в любой точке трубопровода.

Так как при движении продукта по длине трубопровода температура его понижается, то и вязкость в данном случае не является величиной постоянной, вязкость растет вместе с понижением температуры потока. Увеличение вязкости, в свою очередь, приводит к снижению численного значения критерия Рейнольдса. Если критерий Рейнольдса достигает значения 2320, то в этот момент происходит полное изменение режима течения потока, турбулентный режим переходит в ламинарный.

Температуру перехода от турбулентного режима к ламинарному группа авторов [10] предлагает определять по уравнению:

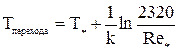       ,                                          (6.7)

где Т_{перехода} – температура перехода при cмене режима движения жидкости, °К;

Т_*, Re_* – произвольно выбранная температура, °К, и критерий Рейнольдса, рассчитанный на основании значения кинематической вязкости потока, соответствующей данной температуре;

k – вязкостная константа, определяемая по уравнению 3.8:

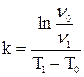    ,                                                                                 (6.8)

где Т₀, Т₁ – произвольные температуры, °К, при которых известны кинематические вязкости ν₀, ν₁.

Зная температуру перехода и вновь применяя уравнение В.П. Шухова, можно рассчитать длину турбулентной зоны при заданных условиях перекачки:

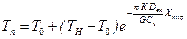                                    (6.9)

где

Т_п – температура перехода, соответствующая смене режима движения потока в трубопроводе, °К;

Х_тур – длина турбулентной зоны.

Исходя из уравнения 6.9, можно записать уравнение 6.10:

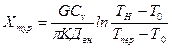                                      (6.10)

Использование в уравнениях 6.9, 6.10 внутреннего диаметра вместо наружного по уравнению 6.6 к какой-либо ошибке при оценке турбулентной зоны не приводит.

С помощью уравнения В.П. Шухова можно графически изобразить линию изменения температуры по длине участка, что позволяет наглядно показать характер её изменения и дает возможность определить температуру в любой точке трубопровода независимо от режима движения потока. Для этого, подставляя в уравнение 6.6 значения L, равные Х₁, Х₂ и т.д., получают текущие значения температуры Т₁, Т₂ и т.д. в заданных точках и наносят их на график в координатах T-L (рис.6.2):

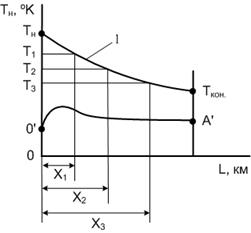
Рис. 6.2 Изменение температуры по длине участка трубопровода

Полученная линия 1 характеризует изменение температуры на заданной длине трубопровода.

Задача № 2