В связи с неизотермичностью процесса перекачки высокопарафинистых нефтей линия гидравлического уклона для заданных участков трубопровода не является прямой линией, которая характерна для ньютоновских жидкостей.
Суть построения линии гидравлического уклона в этом случае в следующем:
1. трубопровод разбивается на ряд подучастков, причем начало каждого – это начальная точка трубопровода;
2. для каждого i-того подучастка определяются потери напора;
3. полученные численные значения hпот i откладываются по оси Н от точки, соответствующей начальному напору станции;
4. по полученным точкам строится линия (рис. 6.4)
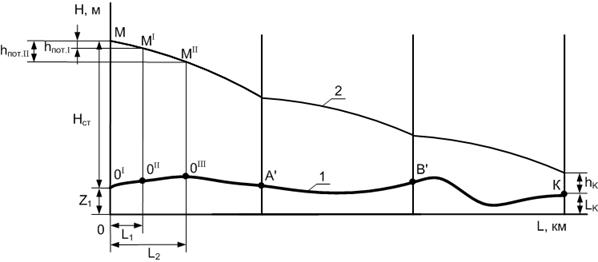
Рис. 6.4 Линия гидравлического уклона для участка МНП
с неизотермическим режимом перекачки:
1 – профиль трубопровода;
2 - линии гидравлического уклона
На рис. 3.4 т.А′, т.В′ - места расположения промежуточных станций подогрева, определенные по уравнению 3.11, участки ОI – OII, ОI – OIII – это подучастки при разбивке трубопровода, им соответствуют hпот I, hпот II, т. К – место расположения следующей НПС или конечного пункта.
Определение потерь напора на каждом подучастке при турбулентном режиме ведется по уравнению Дарси-Вейсбаха, в котором коэффициент гидравлических потерь определяется с учетом неизотермичности потока по длине трубопровода [10].
Уравнения для расчета можно записать:
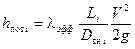, м (6.15)
; 
,
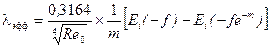
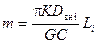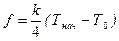где
Li, Dвн I – длина и диаметр подучастков трубопровода, м;
Re0 – критерий Рейнольдса, в котором коэффициент динамической вязкости принимается при температуре окружающей среды;
G – массовый расход потока, кг/с;
С – теплоемкость нефти, Дж/кг·град;
k – вязкостная константа;
Тн – начальная температура нефти, °К;
Т0 – температура окружающей среды, °К;
Еi – функция Эйлера, численные значения функции определяются по справочным таблицам [10].
Если в трубопроводе имеют место участки с разными режимами движения потока, то потери напора можно определить по схеме расчета с учетом турбулентной и ламинарной зон [6. 7]:
1. Для определения гидравлического уклона при изотермическом режиме перекачки принято уравнение (вывод уравнения приведён в приложении Б):
i = b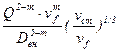 
, (6.16)
где Q - объемный расход, м3/сек;
n f - кинематический коэффициент вязкости при средней температуре потока, м2/сек;
Tcр =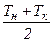 
;
nст - кинематический коэффициент вязкости при температуре стенки, м2/с;
Tн, Tк - начальная и конечная температуры потока на рассматриваемом участке трубопровода, °С;
m, b - коэффициенты, зависящие от режима движения жидкости.
Для ламинарного режима m = 1, b = 128/ p g.
Для зоны гладких труб m = 0,25, b = 0,214/ g.
2. Для изотермического режима рассчитывают hпот по уравнению:
hпот и. р= iL =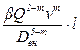 
, (6.17)
отношение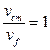 
.
3. Для неизотермического режима hпот н.р определяется как сумма hпот н. р на турбулентном участке и hпот н. р на ламинарном участке по уравнению:
hпот н. р = hпот и.р Dтур + hпот и.р Dл, (6.18)
где Dтур, Dл - поправки на неизотермичность режима при турбулентном и ламинарном режимах движения жидкости.
Аналогично вышесказанному поправка D определяется через функцию Эйлера и для нее получено уравнение:
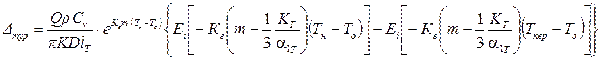
(6.19)
,
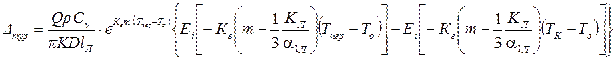где r - плотность жидкости, кг/м3;
С v - теплоемкость жидкости, кдж/кг×град;
D - внутренний диаметр, м;
К - коэффициент теплопередачи от потока к окружающей среде,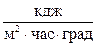 
;
Tн, Tкон - начальная и конечная температуры потока, °С;
Tо - температура окружающей среды, °С;
Кв - вязкостный коэффициент, позволяющий осуществлять пересчет вязкостей при разных температурах, вычисляется по формуле:
Кв =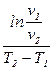 
, (6.20)
l - длина трубопровода между станциями подогрева, м;
Е i - функция Эйлера (справочная величина, данные приведены: Лурье М.В. «Трубопроводный транспорт нефтепродуктов»);
a1 - коэффициент теплоотдачи от потока к стенке трубы, ;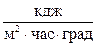
Tпер – температура смены режима, °С.
Обычно a1 » K, поэтому величина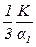 
стремится к нулю.
Коэффициент m при турбулентных режимах равен 0,25, при ламинарном режиме m=1.
Тема 6.3
Дата: 2019-02-18, просмотров: 655.
