Метод неопределенных коэффициентов (системы уравнений). Универсальный, хотя и громоздкий, метод, пригодный для любых корней характеристического полинома.
Левую и правую часть разложения на простые дроби приводят к общему знаменателю, который отбрасывается. Приравнивая коэффициенты при одинаковых степенях s левой и правой частей равенства, составляют систему линейных алгебраических уравнений и решают ее любым известным методом.
Пример. Изображение  разлагается на две дроби
разлагается на две дроби
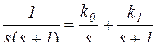
в соответствии с полюсами s 1 = 0; s 2 = -1. Приводим левую и правую части к общему знаменателю, отбрасывая его, группируем коэффициенты, приравниваем коэффициенты при одинаковых степенях s слева и справа
1= k0s +k0 + k1s = (k0 + k1)s + k0
| при s 0 → при s1 → | 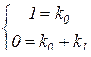
| откуда | k0 = 1 k1 = -1 |
Подставляем значения коэффициентов числителей
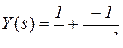
и переходим по таблице соответствия от изображений к оригиналам
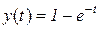 .
.
Метод подстановки полюсов (пригоден только для простых полюсов или дроби с полюсом максимальной кратности).
Формула: 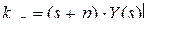
Пример: возьмем ту же функцию 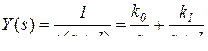 .
.
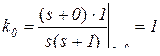 ;
; 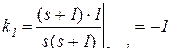 ,
,
получили аналогичный результат. Действия сводятся к тому, что в знаменателе левой части равенства исключают полином с соответствующим полюсом, а в оставшуюся часть подставляют его значение.
Метод вычисления производной (для простых полюсов).
Формула: 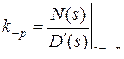 .
.
Пример: возьмем ту же функцию 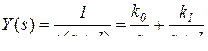 .
.
От знаменателя изображения D ( s ) = s 2 + s вычисляем производную 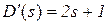 и находим коэффициенты
и находим коэффициенты
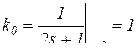 ;
; 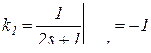 .
.
Метод вычисления производной (для кратных полюсов). Исходное изображение необходимо разделить на две части – часть, содержащую кратные корни, и оставшуюся часть F ( s ). Кратные корни в правой части выражения записывают по убыванию кратности (степени s). Пусть разложение функции имеет вид, где 
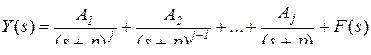 ,
,
тогда формула для вычисления коэффициента числителя Ar (1< r ≤ j ) дроби с кратным корнем
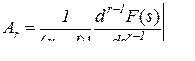 .
.
Пример: дана функция с простым корнем s = -1 и корнем s = 0 с кратностью 3
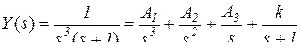 .
.
Остаток после удаления кратных корней равен F ( s ) = 1/( s +1) = ( s +1)-1. Коэффициенты А1 и k определяем другим способом, например, подстановкой полюсов
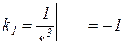 ;
; 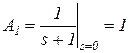 .
.
Остальные коэффициенты
r = 2 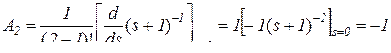 ,
,
r = 3 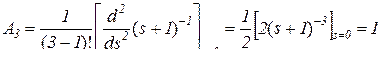
и реакция в целом
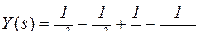 (изображение),
(изображение),
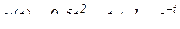 (оригинал).
(оригинал).
Метод вычитания найденной дроби (для кратных полюсов). Пример: дана функция с простым корнем s = -1 и корнем s = 0 с кратностью 3
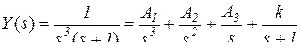 .
.
Находим сразу А1 = 1 любым методом, например, подстановкой полюсов. Вычитаем найденную дробь из левой части
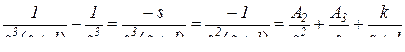
и определяем А2 каким-либо методом, например, подстановкой полюсов
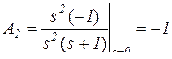 .
.
Снова вычитаем найденную дробь
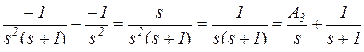 .
.
Осталось найти методом подстановки полюсов А3 = 1 и k = -1, т.е. получены те же результаты, что и в предыдущем примере.
Приложение В
(справочное)
Основы алгебры матриц
Матрицей называется упорядоченный двумерный массив элементов. Матрица обозначается в тексте полужирным шрифтом прописным символом (вектор – строчным), ограничивается скобками вида ( ), [ ], || || и ни в коем случае не одинарными вертикальными линиями | |, т.к. это обозначение соответствует числу (определителю).
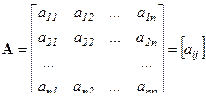 , где , где
| 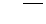 – индекс строки, – индекс строки,
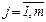 – индекс столбца, – индекс столбца,
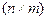 – размер матрицы,
n – число строк,
m – число столбцов. – размер матрицы,
n – число строк,
m – число столбцов.
|
Индексы, представляющие собой число более девяти или выражение, записываются через запятую, например ai , k +1 . Элементы aij | i = j образуют главную диагональ матрицы. Множество элементов, принадлежащее отрезку, соединяющему правый верхний угол с левым нижним, называется побочной диагональю.
Матрица называется:
- противоположной А, если она равна –А;
- транспонированной относительно А, если ее столбцы равны строкам, а строки – столбцам исходной матрицы А (если 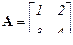 , то
, то 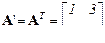 ). Свойства операции транспонирования:
). Свойства операции транспонирования:
(Ak)T=kAT; (A + B)T = AT + BT; (BA)T = ATBT; (AT)T = A;
- квадратной, если n = m, тогда n – порядок матрицы; вектором-столбцом, если m = 1; вектором-строкой, если n = 1; скаляром, если
m = n =1.
Квадратная матрица называется:
- нулевой, если aij = 0, например 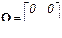 ;
;
- верхней треугольной, если 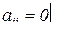 , например
, например 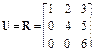 ;
;
- нижней треугольной, если 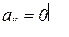 , например
, например 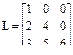 ;
;
- симметричной, если 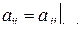 ;
;
- диагональной, если 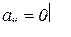 , обозначается
, обозначается  ;
;
- единичной, если 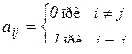 , обозначается E, I, 1, пример
, обозначается E, I, 1, пример 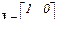 .
.
Размер единичной и нулевой матриц всегда может быть выбран в соответствии с выполняемой операцией.
Матрице можно поставить в соответствие специальные числа: определитель, след, ранг, норму, собственное значение и т.п.
След матрицы равен сумме ее диагональных элементов. Обозначение SpA или TrA, пример: 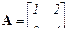 ,
, 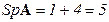 .
.
Правильным называется произведение n элементов квадратной матрицы с последовательно возрастающими индексами строк и столбцов. При нарушении последовательности индексов строк или столбцов произведение берется с минусом.
Определителем матрицы называется алгебраическая сумма всех ее правильных произведений с учетом знака. Определитель (детерминант) обозначается D, Δ, detA, |A|. Пример: 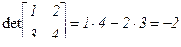 .
.
Определитель существует только для квадратной матрицы, он не изменяется при транспонировании матрицы. Определитель произведения матриц равен произведению их определителей. Матрица, определитель которой равен нулю, называется особой (вырожденной, сингулярной), матрица с ненулевым определителем соответственно регулярной (неособой, невырожденной).
Вычеркнем в матрице А i-строку и j-столбец. Определитель полученной матрицы (n-1)-го порядка называют минором элемента aij в определителе матрицы А и обозначают через Mij. Алгебраическое дополнение элемента aij равно 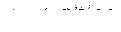 .
.
Порядок наибольшей подматрицы, минор которой не равен нулю, называется рангом матрицы А (обозначается RangA или RankA). Матрица является неособой, если имеет полный ранг, равный ее порядку. Ранг матрицы не изменяется при транспонировании. Пример: определитель матрицы 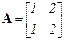 равен Δ2 = 0, однако есть минор первого порядка Δ1 = 2 ≠ 0, поэтому ранг матрицы RankA = 1.
равен Δ2 = 0, однако есть минор первого порядка Δ1 = 2 ≠ 0, поэтому ранг матрицы RankA = 1.
Если матрица приведена к трапецеидальному виду, ранг матрицы равен числу ее диагональных элементов. Пример:


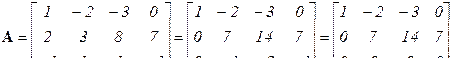
Ненулевых диагональных элементов триангулированной матрицы два (1 и 7), поэтому RankA = 2.
Матрицы равны при равенстве их размерностей и соответственных элементов. Складывать можно лишь матрицы с одинаковым числом строк и столбцов. Суммой двух матриц является матрица, каждый элемент которой равен сумме их соответственных элементов. Чтобы умножить матрицу на число, нужно каждый ее элемент умножить на это число. Произведение двух матриц определено, если число столбцов левой матрицы равно числу строк правой матрицы. Число строк результирующей матрицы равно числу строк левой матрицы, а число столбцов – числу столбцов правой матрицы. Матрицы называются сцепленными, если их произведение существует, и перестановочными, если результат их перемножения как слева, так и справа одинаков. Результат умножения как слева, так и справа любой матрицы на единичную всегда равен исходной матрице, на нулевую – нулевой. Операция деления соответствует умножению на обратную матрицу.
Квадратная матрица А называется обратимой, если существует такая матрица А-1, для которой АА-1 = А-1А = 1. Матрица А-1 называется обратной к А. Матрица обратима только тогда, когда не является особой (когда ее определитель не равен нулю). Свойства обратной матрицы: (А-1)-1 = А, (АВ)-1 = А-1В-1.
Поскольку 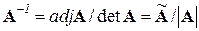 , где в числителе дроби находится присоединенная матрица, один из методов определения обратной матрицы связан с вычислением присоединенной матрицы (матрицы алгебраических дополнений). Присоединенной к матрице А называется матрица, полученная путем замены каждого элемента исходной матрицы его алгебраическим дополнением и транспонирования полученной матрицы.
, где в числителе дроби находится присоединенная матрица, один из методов определения обратной матрицы связан с вычислением присоединенной матрицы (матрицы алгебраических дополнений). Присоединенной к матрице А называется матрица, полученная путем замены каждого элемента исходной матрицы его алгебраическим дополнением и транспонирования полученной матрицы.
Пример: 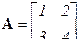 ,
, 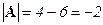 ,
,
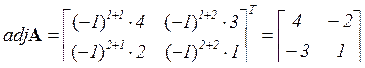 ,
,
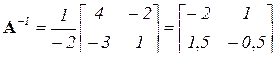 .
.
Существует простое мнемоническое правило учета знака алгебраических дополнений (шахматка): после вычисления миноров знаки элементов матрицы изменяются в шахматном порядке, начиная с (+) у левого диагонального элемента. Кроме того, для вычисления присоединенной матрицы второго порядка достаточно в исходной матрице элементы главной диагонали поменять местами, а у элементов побочной диагонали поменять знаки.
Число λ называется собственным значением (характеристическим числом) квадратной матрицы А порядка n, если можно подобрать такой n-мерный ненулевой вектор х, что Ах = λх. Если раскрыть определитель матрицы [λ·1 - A], то получится многочлен n-ой степени относительно λ
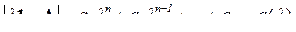 ,
,
называемый характеристическим многочленом матрицы А, у которого а0 = 1, а an = |A|. Уравнение 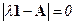 называется характеристическим уравнением матрицы А. Иногда для него используется запись
называется характеристическим уравнением матрицы А. Иногда для него используется запись 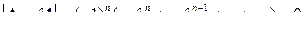 .
.
Пример: матрица 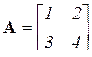 ,
,
характеристическая матрица
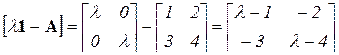 ,
,
характеристический полином 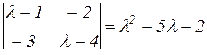 ,
,
собственные значения λ1 = 5,415; λ2 = -0,415.
Матрицы А и А* подобны, если равны их характеристические полиномы a(λ) и собственные значения si
det(λ1 - A) = det(λ1 - A*) = a(λ);
λi {A} = λi {A*} = si.
Приложение Г
(справочное)
Типовые полиномы
В процессе синтеза систем управления используют характеристические полиномы, образуемые по известному закону, для которых заранее определены показатели качества (время регулирования, перерегулирование). Не следует лишь забывать, что нули передаточной функции при этом должны отсутствовать, в противном случае все показатели изменяются.
Полином Баттерворта определяется формулой
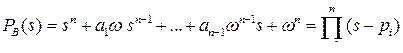 ,
,
где p i – корни полинома, расположенные слева от мнимой оси комплексной плоскости в вершинах правильного 2n-угольника, ω – положительное число, задаёт радиус распределения корней. Полиномы первого-шестого порядка приведены в таблице Г.1.
Таблица Г.1
| n | Вид полинома Баттерворта | tрег, с | σ, % |
| 1 | 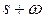
| 3,0 | 0,0 |
| 2 | 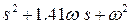
| 2,9 | 4,5 |
| 3 | 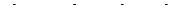
| 6,0 | 8,0 |
| 4 | 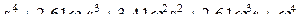
| 6,8 | 11,0 |
| 5 | 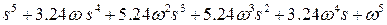
| 7,7 | 13,5 |
| 6 | 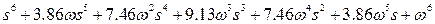
| 10,8 | 14,3 |
Нормированные полиномы Баттерворта получаются при ω = 1, для них основные показатели качества даны в таблице. Для ненормированных полиномов перерегулирование не изменяется, а время регулирования нужно разделить на ω.
Полином Ньютона определяется формулой биномиального разложения
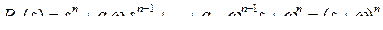 ,
,
где ω – положительное число, ai – биномиальные коэффициенты. Полиномы первого-шестого порядка на основе бинома Ньютона приведены в таблице Г.2. Полиномы имеют кратные вещественные отрицательные корни, равные –ω, поэтому перерегулирование для них равно нулю. Нормированные полиномы Ньютона получаются при ω = 1, время регулирования для них указано в таблице. Для ненормированных полиномов время регулирования нужно разделить на ω.
Таблица Г.2
| n | Вид полинома Ньютона | tрег, с |
| 1 | 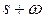
| 3,0 |
| 2 | 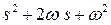
| 4,8 |
| 3 | 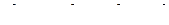
| 6,3 |
| 4 | 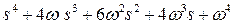
| 7,8 |
| 5 | 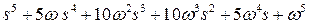
| 9,2 |
| 6 | 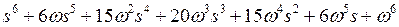
| 10,5 |
Выбор числа ω для полиномов Баттерворта или Ньютона соответствующей степени производится по формуле ω = tтаб/tзад, где tтаб – время регулирования нормированного полинома, взятое из таблицы, tзад – заданное время регулирования.
Содержание
| Введение | 3 |
| 1 Одномерные линейные непрерывные системы | 4 |
| 1.1 Передаточная функция | 4 |
| 1.2 Временные характеристики | 14 |
| 1.3 Частотные характеристики | 22 |
| 1.4 Устойчивость непрерывных стационарных систем | 30 |
| 1.5 Качество непрерывных стационарных систем | 45 |
| 2 Многомерные системы регулирования | 60 |
| 2.1 Переход к пространству состояний | 60 |
| 2.2 Канонические представления | 62 |
| 2.3 Описание по структурной схеме | 65 |
| 2.4 Синтез структурной схемы | 69 |
| 2.5 Основные матричные функции | 72 |
| 2.6 Решение уравнения движения | 74 |
| 2.7 Вычисление фундаментальной матрицы | 77 |
| 2.8 Управляемость и наблюдаемость систем | 81 |
| 2.9 Наблюдатели состояния | 84 |
| 2.10 Проектирование модального регулятора | 88 |
| 2.11 Преобразования подобия | 92 |
| 3 Ответы | 96 |
| Литература | 102 |
| Приложение А Таблица соответствия оригиналов и изображений | 103 |
| Приложение Б Расчет числителей простых дробей | 104 |
| Приложение В Основы алгебры матриц | 107 |
| Приложение Г Типовые полиномы | 111 |
Дата: 2019-02-19, просмотров: 503.