Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

1.5.1 Прямые оценки качества регулирования

Прямые оценки качества определяются по переходной характе­ристике, т.е. реакции системы на единичный скачок при нулевых начальных условиях (рисунок 1.55).

Время регулирования t_рег  измеряется от начала переходного процесса до момента, после которого характеристика не отклоняется от установившегося значения более, чем на величину допустимой ошибки ∆ (обычно 5 %, реже 2 % от установившегося значения). Следует указывать, при какой зоне Δ получено время регулирования.

Перерегулирование σ – величина максимального относительного заброса переходной характеристики от начальной величины за линию установившегося значения (в относительных единицах 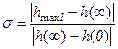или %)

 

 или .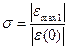

 

 

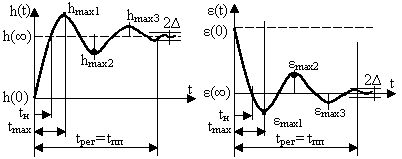
а) – выходная величина y(t) б) – ошибка регулирования ε(t)

или h(t)                              или отклонение δ(t)

Рисунок 1.55

 

Если начальное и конечное значения характеристики равны нулю или одинаковы (и приняты условно за 0), возможны два способа оценки. При наличии разнополярных значений перерегулирование равно отношению величины второго экстремума к величине первого (рисунок 1.56, а), а если колебание одно (рисунок 1.56, б), то перерегулирование равно отношению величины максимального отклонения к величине входного воздействия (обычно это единица). Зону Δ для оценки времени регулирования в первом случае определяют от значения первого максимума, во втором случае – от величины входного воздействия.

 

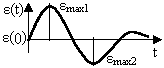
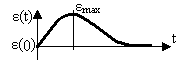
а                                                  б

Рисунок 1.56

 

Время нарастания t_н определяется: для процессов с перерегулированием как время от начала процесса до момента пересечения кривой линии установившегося значения; для любых процессов как время между моментами достижения заданных уровней установившегося значения (например, 10 и 90 %). Поэтому при оценке времени нарастания следует указывать, каким способом оно получено.

Время достижения первого максимума t_max (подразумевается, что первый максимум кривой является и наибольшим из всех).

Коэффициент колебательности N – число забросов переходной характеристики через линию установившегося значения за время ре­гулирования, рекомендуется не более одного-двух забросов.

Степень затухания (демпфирования) – величина относительного уменьшения ψ = (h_{max 1} - h_{max 3})/(h_{max 1} – h(∞)) амплитуды максимальных забросов выходной величины за один период Т_к, удовлетворительной считают систему с ψ = 0,75...0,95.

Установившаяся ошибка ε(∞) равна разнице между предписанным и действительным значениями выходной величины после окончания переходного процесса.

Пример 1. Оценить время регулирования и перерегулирование для системы с передаточной функцией k/(s + 2).

Поскольку полюс α = -2 действительный, без мнимой части, колебаний не будет и перерегулирование σ = 0. Переходный процесс описывается зависимостью k(1 - e^αt) и заканчивается при достижении величины 0,95k, т.е. когда выполняется условие e^αt = Δ = 0,05. Отсюда t_рег =ln(Δ)/α = ln(0,05)/(-2) = 1,498 с.

Пример 2. Определить величину перерегулирования и времени регулирования (рисунок 1.57)

 

 

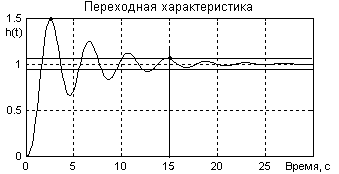
Рисунок 1.57

 

Перерегулирование σ = (1,5 – 1,0)/1,0 = 0,5 или 50 %. Для определения времени регулирования проводим параллельно линии установившегося значения две прямые на уровне h_уст ±Δ = 1±0,05×1 = 1±0,05. По точке последнего вхождения кривой в зону 2Δ получаем t_рег = 15 с.

Задания для самостоятельного решения.

1.5.1.1 Оценить качество регулирования для звена с передаточной функцией .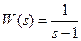

1.5.1.2 Сформулировать условия отсутствия перерегулирования в системе с дифференциальным уравнением .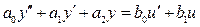

1.5.1.3 Определить величину перерегулирования системы (рисунок 1.58) от скачка задания

 

 

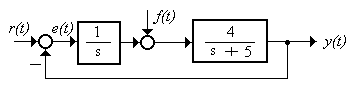
Рисунок 1.58

 

1.5.1.4 Найти все показатели качества регулирования (рисунок 1.59)

 

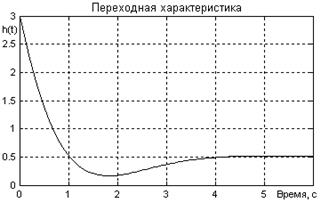
Рисунок 1.59

 

1.5.1.5 Оценить основные показатели качества регулирования (рисунок 1.60) относительно возмущения

 

 

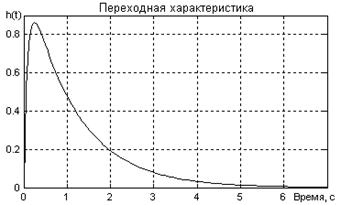
Рисунок 1.60

 

1.5.1.6 Найти время регулирования t_рег, степень демпфирования и величину перерегулирования σ по переходной характеристике выхода системы относительно возмущения (рисунок 1.61)

 

 

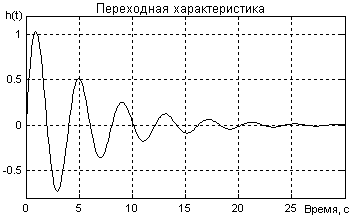
Рисунок 1.61

 

1.5.2 Корневые методы оценки качества регулирования

Доминирующими называются левые полюса системы, ближайшие к мнимой оси. Степень устойчивости α_min (или η) равна модулю их действительной части (рисунок 1.62). Для оценки времени регулирования t_рег находят сначала степень устойчивости системы, откуда при ошибке ∆=5 % t_рег ≈ 3/|α_min|. При заданной зоне ошибки 2 % вместо коэффициента 3 берут приблизительно 4.

 

 

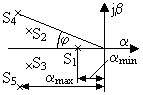
Рисунок 1.62

 

Найдя степень колебательности системы 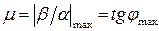, определяют значение перерегулирования 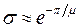. Для расчета μ выбирают комплексный корень (полюс), у которого отношение мнимой части к действительной максимально. При единственной паре комплексных корней необходимость выбора отпадает. При нескольких парах комплексных корней максимальное значение μ у того корня, который первым встречается лучу, проведенному из начала координат по положительной мнимой полуоси и поворачиваемому против часовой стрелки.

Показатели качества определяют только для устойчивых систем. Если система имеет нуль, равный полюсу, то они взаимно компенсируются и данная составляющая не учитывается (выпадает из переходного процесса).

Пример 1. Оценить показатели качества регулирования системы, имеющей нуль -0,125, полюса -1,5 ± 6j; -0,125 и коэффициент передачи 1,2.

Коэффициент передачи на относительные показатели не влияет. Нуль -0,125, равный полюсу, взаимно с ним компенсируется. Следовательно, доминирующими являются комплексно-сопряженные полюса -1,5 ± 6j, откуда t_рег ≈ 3/|α_min| = 3/1,5 = 2 с, степень колебательности системы 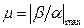 = 6/1,5 = 4 и перерегулирование  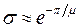= 0,456 или 45,6 %.

Пример 2. Оценить перерегулирование и время регулирования системы 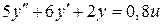 с законом управления u = 2(r – y).

Подставляя значение u в соответствии с законом регулирования, получим дифференциальное уравнение 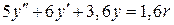. Нули отсутствуют, из характеристического уравнения  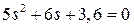находим полюса -0,6 ± j0,6. Отсюда t_рег ≈ 3/|α_min| = 3/0,6 = 5 c, а перерегулирование  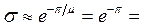0,043 или 4,3 %.

Задания для самостоятельного решения.

1.5.2.1 Оценить степень устойчивости и степень колебательности системы с D(s) = (s + 1)(s² + 2s + 2).

1.5.2.2 Найти показатели качества системы с характеристическим уравнением D(s) = s³ + s² + 2s + 3 = 0.

1.5.2.3 Оценить степень устойчивости и степень колебательности системы (рисунок 1.63)

 

 

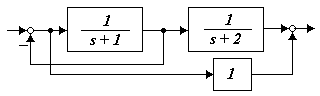
Рисунок 1.63

 

1.5.2.4 Найти время регулирования системы (рисунок 1.64)

 

 

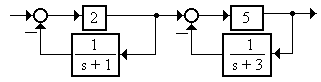
Рисунок 1.64

 

1.5.2.5 Найти t_рег и σ системы (рисунок 1.65), если k = 3

 

 

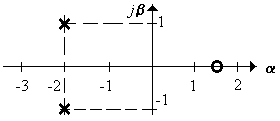
Рисунок 1.65

 

1.5.2.6 Рассчитать перерегулирование и время регулирования для системы (рисунок 1.66)

 

 

Рисунок 1.66

 

1.5.2.7 Оценить приблизительно t_рег и σ системы (рисунок 1.67) для произвольного значения k

 

 

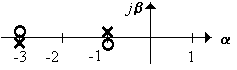
Рисунок 1.67

 

1.5.3 Частотные методы оценки качества регулирования

Особые частоты: ω₊ – граница интервала частот положительности ВЧХ, ω₀ – частота собственных колебаний, ω_сущ – граница интервала существенных частот, вне которого текущее значение функции уже не превышает (0,05…0,1)P(0).

Общие принципы оценки качества по вещественной частотной характеристике P ( ω ):

- P (0) = h (∞) = k _уст – конечное значение переходной характеристики численно равно начальному значению ВЧХ;

- P (∞) = h (0) – начальное значение переходной характеристики численно равно конечному значению ВЧХ;

- a · P (ω) ÷ a · h ( t ) – кратность изменения масштаба ВЧХ и переходной характеристики одинакова;

- P ( a ·ω) ÷ h ( t / a ) – расширение полосы рабочих частот ведет к соразмерному повышению быстродействия системы;

- время регулирования π/ω₊ < t _рег < 4π/ω₊,

- перерегулирование σ определяется по форме ВЧХ:

а) если ВЧХ монотонно убывает, то перерегулирование σ = 0;

б) если ВЧХ является положительной невозрастающей функцией, то перерегулирование σ < 18 %;

в) если ВЧХ имеет подъем от P (0), то ;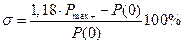

г) если ВЧХ имеет отрицательный минимум со значением более 0,1 P (0), то с его учетом ;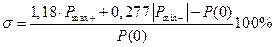

д) если ВЧХ терпит разрыв при ω=ω₀, система совершает незатухающие колебания, t_рег → ∞ и показатели качества не определяются.

При оценке качества регулирования по АЧХ обычно вычисляют значение частотного показателя колебательности, равное отношению максимума характеристики к ее начальному значению М = А_м/А(0). При М = 1 переходная характеристика системы не колебательна, при М → ∞ система находится на границе устойчивости, наблюдаются незатухающие колебания с частотой ω₀. Оптимальными считаются значения М = 1,1..1,5, которым соответствует перерегулирование 10-30 % и запас по фазе 30-50°.

Пример 1. Оценить значение частотного показателя колебательности системы по её АЧХ (рисунок 1.68).

 

 

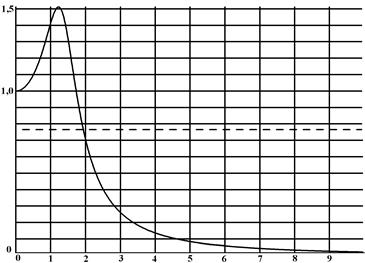
Рисунок 1.68

 

Максимальное значение АЧХ равно 1,51, следовательно, показатель колебательности М = 1,51/1,0 = 1,51, что ещё удовлетворяет минимальному запасу по фазе 30° и перерегулированию 30 %.

Пример 2. Найти значение перерегулирования и времени регулирования системы по заданной АФЧХ (рисунок 1.69)

 

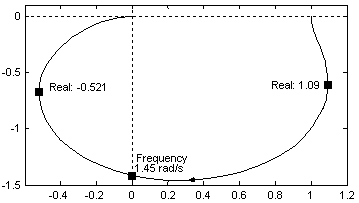
Рисунок 1.69

 

Частота ω₊ = 1,45 рад/с, положительный максимум ВЧХ равен 1,09 при начальном значении Р(0) = 1,0, отрицательный минимум 0,521. Отсюда получаем перерегулирование

 

 =

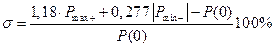= (1,18*1,09 + 0,277*0,521 – 1,0)*100 = 43,1 %

 

и время регулирования не более 4π/ω₊ = 4*3,1415926/1,45 = 8,67 с.

Задания для самостоятельного решения.

1.5.3.1 Оценить t_рег и σ системы с ПФ W(s) = 4/(s² + 6s +8), используя частотный метод.

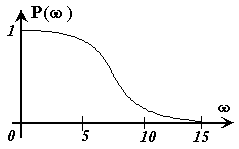
1.5.3.2 Найти оценки показателей качества по ВЧХ (рисунок 1.70), считая ω₊ = ω_сущ

 

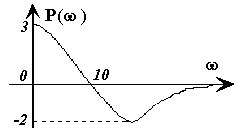
Рисунок 1.70	Рисунок 1.71

 

1.5.3.3 Найти по вещественной частотной характеристике P(w) показатели качества переходного процесса s, t_рег (рисунок 1.71)

1.5.3.4 Найти частотным методом показатели качества s и t_рег после замыкания системы, если передаточная функция разомкнутой системы равна W(s) = 9/(s² +11s + 1).

1.5.3.5 Оценить частотным методом установившуюся ошибку системы с передаточной функцией W(s) = 9/(s³ +2s² +6s + 10).

1.5.4 Интегральные оценки качества переходных процессов

Интегральные показатели качества регулирования дают совокупную оценку быстродействия и колебательности без вычисления их значений. Они характеризуют отклонение реального переходного процесса от заданного идеального.

Интегральная линейная оценка (ИЛО) определяется площадью отклонения реального процесса от идеального ступенчатого. Для обеспечения требуемых динамических свойств САУ необходимо выразить величину J₁ через коэффициенты передаточной функции системы

,

 

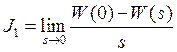где W(0) – значение передаточной функции в установившемся режиме (при s = 0), а затем найти оптимальные значения варьируемых параметров, соответствующих минимуму J₁.

Пример 1. Для системы с передаточной функцией

 

 

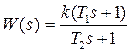
линейная интегральная оценка

 

 

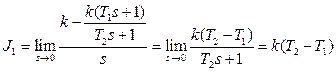
зависит от соотношения постоянных времени Т₁ и Т₂. Минимум оценки достигается при их равенстве.

Задания для самостоятельного решения.

1.5.4.1 При каком значении k интегральная линейная оценка минимальна, если ПФ системы равна W(s) = ks/(T s + 1).

1.5.4.2 Оценить вид интегральной линейной оценки для системы с передаточной функцией W(s) = (b₀s + b₁)/(a₀s² + a₁s + a₂).

1.5.4.3 Найти интегральную линейную оценку для системы с передаточной функцией W(s) = (s + 1)/(s² +2s + 1).

1.5.4.4 Чему равна интегральная оценка J ₁ для системы с передаточной функцией W(s) = k/(T s + 1).

1.5.4.5 Оценить влияние T на величину J ₁, если передаточная функция системы равна W(s) = 2s/(Т s² +2s + 2).

 

1.5.5 Точность в установившемся режиме

Установившаяся ошибка характеризует точность системы в ста­тическом режиме и равна отклонению действительного значения ре­гулируемой величины от заданного. Система с нулевой установившейся ошибкой ε(∞) = 0 называется астатической, а при ε(∞) ≠ 0 и система и ошибка называются статическими.

Ошибка зависит от вида входного воздействия, места его при­ложения и степени астатизма ν (числа нулевых полюсов) разомкнутой системы. По умолчанию подразумевают вход задания r(t) и вид воздействия скачок 1(t) при нулевых начальных условиях, в ином случае условия получения ошибки должны оговариваться специально.

Передаточная функция ошибки воспроизведения задания определяется по ПФ разомкнутой системы как W_ε(s) = 1/(1 + W_раз(s)), по передаточной функции замкнутой системы как W_ε(s) = 1 – W_зам(s).

Относительная величина установившейся ошибки называется коэффициентом статизма (статизмом) системы по соответствующему каналу:

 

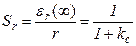– статизм от задания r ( t ),

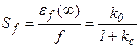– статизм от возмущения f( t ).

 

Здесь k ₀ – коэффициент усиления объекта регулирования. Ошибку регулирования и статизм можно уменьшить, увеличивая общий коэффициент усиления системы k _c, а по заданной величине статизма (относительной статической ошибки) системы можно выбрать требуемый коэффициент усиления.

Интеграторы с ПФ вида k/s, добавляемые вне цепи прямой связи сигнала ошибки, увеличивая порядок астатизма разомкнутой системы, позволяют полностью устранить ошибки статическую, по скорости, по ускорению.

Установившийся динамический режим имеет место при возму­щенном движении системы с момента затухания свободной состав­ляющей переходного процесса. Если входное воздействие аппроксимируется полиномом от t, т.е. разлагается в степенной ряд

 

,

 

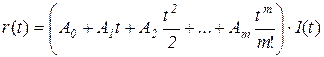для расчета вынужденной составляющей ошибки используют метод коэффициентов ошибок. По этому методу передаточную функцию ошибки представляют в виде аналогичного ряда

 

,

 

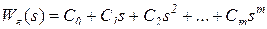где С₀ – коэффициент статической (позиционной) ошибки от k×1(t);

С₁ – коэффициент ошибки по скорости от линейной функции kt,

С₂ – коэффициент ошибки по ускорению от функции kt².

Сравнивая две формы записи передаточной функции ошибки, находят значения коэффициентов ошибок (в обоих случаях полиномы нужно начать со свободного члена, а дробь пронормировать по свободному члену знаменателя)

;

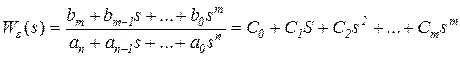s⁰ → b_m=a_nC₀  → ,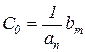

s¹ →                 → ,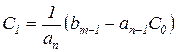

s² →  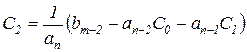               →  и т.д.

Обычно вычисляют не более трех первых коэффициентов оши­бок. Коэффициенты передачи составляющих входного воздействия вычисляются по ПФ разомкнутой системы и называются:

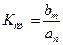                                – позиционная добротность;

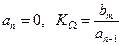                    – добротность по скорости;

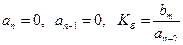       – добротность по ускорению.

Пример 1. Пусть допустимая статическая ошибка воспроизведения скачка задания не должна превышать значения ε(∞) = 2 % или ε(∞) = 0,02. Для этого необходимо иметь полный коэффициент усиления системы не менее

 

.

 

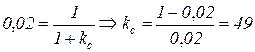Пример 2. Определить полную статическую ошибку для системы (рисунок 1.72), полагая, что r ( t ) = 1(t), f ( t ) = 2,2(t).

 

 

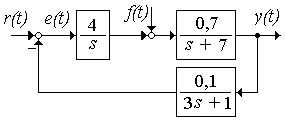
Рисунок 1.72

 

Выражение для суммарной ошибки в операторной форме

 

.

 

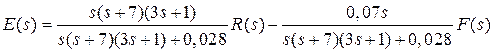Поскольку изображения входных сигналов равны 1/s и 2,2/s, полная статическая ошибка будет равна 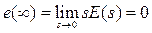. Благодаря интегратору 4/s, значение ошибки от величины задания r(t) и возмущения f(t) не зависит. Система является астатической относительно обоих воздействий.

Пример 3. Определить три первых коэффициента ошибки, вынужденную составляющую ошибки от воздействия 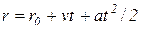 и добротность по скорости для системы, имеющей в разомкнутом состоянии ПФ .

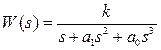Находим передаточную функцию по каналу ошибки

 

.

 

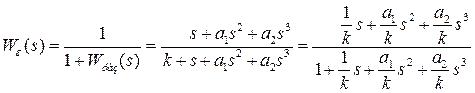Используя нормированную по k передаточную функцию, найдем три первых коэффициента ошибок

 

,         ,      .

 

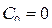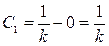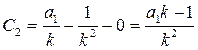В общем виде вынужденная составляющая ошибки воспроизведения задающего воздействия равна 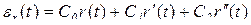. Для задающего воздействия  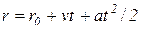находим производные 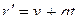,  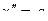и установившуюся динамическую ошибку в любой момент времени 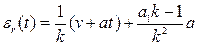. Добротность по скорости вычисляем по ПФ разомкнутой системы .

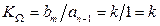Задания для самостоятельного решения.

1.5.5.1 Для системы (рисунок 1.73) определить относительную статическую и скоростную ошибки при r(t)=5t×1(t)

 

 

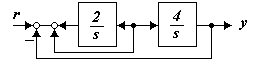
Рисунок 1.73

 

1.5.5.2 Оценить статизм системы (рисунок 1.74) после замыкания (k = 2)

 

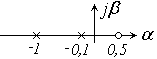
Рисунок 1.74

 

1.5.5.3 Рассчитать коэффициенты ошибок системы (рисунок 1.75) относительно задания

 

 

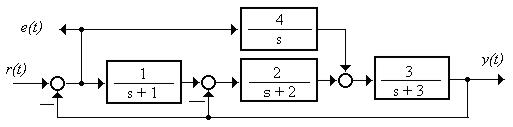
Рисунок 1.75

 

1.5.5.4 Найти коэффициенты ошибок по заданию С₀, С₁, С₂ системы (рисунок 1.76)

 

 

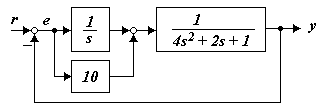
Рисунок 1.76

 

1.5.5.5 Определить величину установившейся ошибки в системе (рисунок 1.77)

 

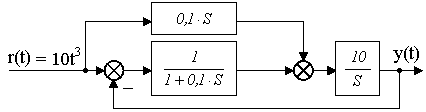
Рисунок 1.77

 

1.5.5.6 Для САУ с передаточной функцией разомкнутой системы 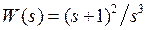 вычислить три первых коэффициента ошибок и оценить величину установившейся ошибки, если r(t)=2t².

1.5.5.7 Определить величину установившейся ошибки в системе (рисунок 1.78) при входном воздействии r(t)=10t².

 

 

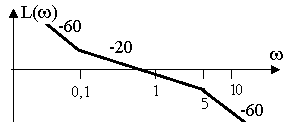
Рисунок 1.78

 

1.5.5.8 Определить величину установившейся ошибки в системе, если r(t)=10t и передаточная функция разомкнутой системы равна

 

.

 

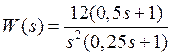1.5.5.9 Написать общую формулу для определения при полиномиальном входном воздействии статической ошибки системы (рисунок 1.79). Определить статическую ошибку данной системы при r(t)=1+2t.

 

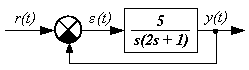
Рисунок 1.79