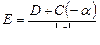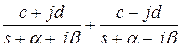Модальным называется регулятор, параметры которого выбраны по желаемому характеристическому многочлену замкнутой системы управления. Полагаем, что все переменные состояния объекта управления доступны для измерения, и рассмотрим случай, когда используется П-регулятор. Модель объекта управления
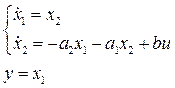
Закон управления для объекта второго порядка имеет вид
u = Kr – k 1 x 2 – k 2 x 1
где K – коэффициент усиления П-регулятора, r – задание, k 1 , k2 – коэффициенты обратных связей регулятора по переменным состояния.
Подставив значение u в уравнение состояния, получим систему уравнений, которая описывает замкнутую систему управления
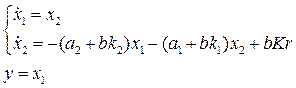 ,
,
и характеристический полином замкнутой системы
D(s) = s2 + (a1 + bk1)s + (a2 + bk2).
Неизвестные коэффициенты k1 и k2 обратных связей по переменным состояния объекта можно определить из равенства полиному желаемого вида Dж(s). Последний либо выбирают на основе заданных значений перерегулирования s % и времени регулирования tп. из типовых (приложение Г), либо рассчитывают самостоятельно. Например, параметры качества регулирования σ = 4,5 %, tр = 2,9 с при отсутствии нулей обеспечит нормированный полином Баттерворта второго порядка
D ж ( s ) = s2 + d 1 s + d 2 = s 2 + 1,14 s + 1.
Приравняв коэффициенты полиномов при одинаковых степенях s, получим k1 = ( d 1 – a 1 )/ b , k 2 = ( d 2 – a 2 )/ b. Расчет существенно упрощается, если объект представлен в канонической форме управляемости с b = 1.
Коэффициент усиления K обычно находят из условия нулевой статической ошибки: либо по коэффициентам передаточной функции bK/( a 2 + k 2 ) = 1, откуда K = (a2 + k 2 )/ b = dn / bm, либо из инверсии матричной передаточной функции K = (c(-A)-1b)-1 при s = 0.
Если для измерения доступна только одна величина на выходе y ( t ), для создания обратных связей по переменным состояния устанавливают наблюдатель, либо в цепи главной обратной связи системы используют ПД-регулятор (форсирующее звено) с эквивалентной передаточной функцией Heq ( s ).
Пример 1. Рассчитать параметры модального регулятора для объекта
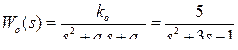
при требованиях к качеству регулирования tп £ 3 с; s = 0 % , е(∞) =0. Регулятор состоит из двух частей: обеспечивающей статические характеристики системы W s ( s ) и обеспечивающей динамические характеристики Wd ( s ) (рисунок 2.25), для измерения доступна только выходная переменная y объекта.
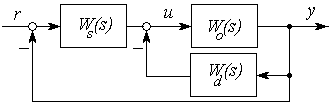
Рисунок 2.25
Выберем интегратор (И-регулятор) в качестве Ws = k/ s, чтобы обеспечить нулевую статическую ошибку е(∞) = 0; пусть составляющая регулятора, обеспечивающая заданные динамические свойства равна Wd( s ) = (d1s +d2)/ko; здесь k, d1, d2 – неизвестные коэффициенты, ko – коэффициент передачи объекта регулирования.
Тогда характеристическое уравнение замкнутой системы равно
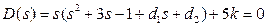
или
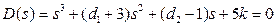
Выберем распределение корней, обеспечивающее заданное качество процессов, например, λ1 = -2; λ2 = -2,5; λ3 = -3 (все действительные полюса обеспечат нулевое перерегулирование и время регулирования не более 3/2 = 1,5 с). Сформируем желаемое характеристическое уравнение третьего порядка
D(s) = (s - λ1)(s - λ2)(s - λ3) = s3 + 7,5s2 + 18,5s + 15 = 0.
Приравнивая коэффициенты при соответствующих степенях s, получим расчетные соотношения d1 + 3 = 7,5; d2 – 1 = 18,5; 5k = 15. Отсюда находим параметры регулятора d1 = 4,5; d2 = 19,5; k = 3.
Пример 2. ПФ объекта регулирования после нормирования имеет вид
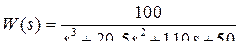 ,
,
заданные показатели качества: время регулирования 6 с, перерегулирование 0,02, выбрать параметры модального регулятора. Поскольку объект представлен передаточной функцией и не все переменные состояния измеряются, формируем наблюдатель состояния с параметрами b = 100, a10 = 20,5, a20 = 110, a30 = 50.
Исходя из требований к процессу регулирования замкнутой системы, выбираем корни s 1 , s 2 ... sn и определяем эталонный (желаемый) характеристический полином с коэффициентами a 1 ... an. Характеристический полином третьей степени содержит один действительный корень и два комплексных сопряженных, по последним, полагая их доминирующими, и будем формировать показатели качества регулирования.
При заданном времени регулирования tрег = 6 с степень устойчивости для ошибки Δ = 5 % равна αmin = 3/6 = 0,5, отсюда действительная часть комплексного корня будет равна -0,5. Действительный корень принимаем в 10 раз большим, т.е. -5, чтобы исключить его влияние на переходный процесс. По заданной величине перерегулирования σ = 0,02 вычисляем степень колебательности μ = -π/ln(σ) =
= -3,1415926/ln(0,02) = 0,803, после чего можно вычислить мнимую часть комплексного корня β = μ∙αmin = 0,803∙0,5 = 0,401.
По значениям корней -5 и -0,5 ± j0,401 находим вид желаемого характеристического полинома
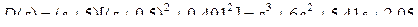 .
.
Из условия нулевой ошибки регулирования значение коэффициента усиления регулятора K = an / b = 2,05/100 = 0,0205. Значения коэффициентов обратной связи по переменным состояния равны
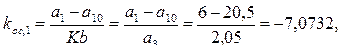
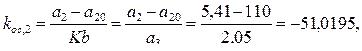
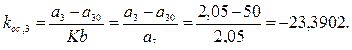
Замкнутая система регулирования (рисунок 2.26) содержит объект управления на выходе U ( t ), наблюдатель в форме, соответствующей каноническому управляемому представлению, П-регулятор с коэффициентом усиления К и обратными связями koc по переменным состояния, формируемым наблюдателем.
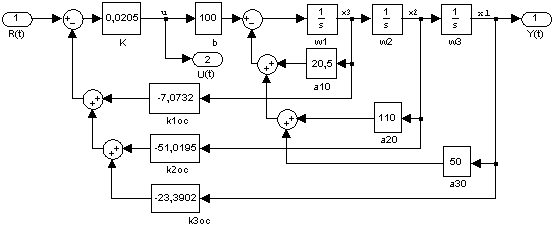
Рисунок 2.26
Передаточная функция замкнутой системы регулирования равна
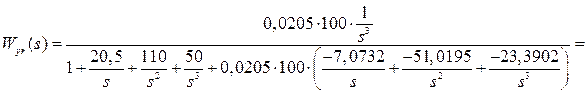
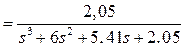 .
.
Расчет подтверждает, что установившаяся ошибка отсутствует, так как коэффициент передачи в установившемся режиме равен 2,05/2,05 = 1, а полученный характеристический полином системы регулирования равен желаемому. При единственной обратной связи
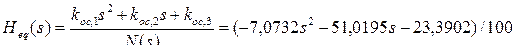 .
.
Задания для самостоятельного решения.
2.10.1 Выбрать значения параметров регулятора для объекта с передаточной функцией 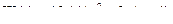 при следующих требованиях к качеству регулирования ε(∞) = 0; σ ≤ 20 %; tрег ≈ 1 с.
при следующих требованиях к качеству регулирования ε(∞) = 0; σ ≤ 20 %; tрег ≈ 1 с.
2.10.2 Выбрать регулятор при заданных показателях качества регулирования ε(∞) = 0; σ ≤ 30 %; tрег ≈ 1 с для объекта
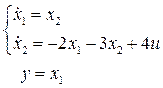
2.10.3 Выбрать регулятор при заданных показателях качества регулирования ε(∞) = 2 % от r(t); σ = 0 %; tрег ≤ 3 с для объекта с передаточной функцией 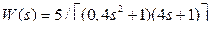 .
.
2.10.4 Выбрать регулятор при заданных показателях качества регулирования ε(∞) = 5 % от r(t); σ = 0 %; tрег ≤ 5 с для объекта с передаточной функцией 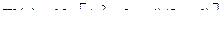 .
.
2.10.5 Выбрать регулятор при заданных показателях качества регулирования ε(∞) = 0; σ ≤ 20 %; tрег ≈ 3 с для объекта
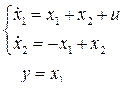
2.10.6 Записать желаемый характеристический полином третьего порядка по требованиям к качеству регулирования tрег ≤ 3 с; μ ≤ 1,5.
2.11 Преобразования подобия
При анализе и синтезе многомерных систем необходимо уметь переходить от одной формы к другой – поскольку все эти системы подобные, такой переход называется преобразованием подобия или базиса.
Один из путей перехода, приемлемый для одномерной системы – составить по матрицам A, b, c передаточную функцию системы, а по ней записать требуемое представление в пространстве состояний.
В общем же случае используют матрицу перехода или преобразования базиса Р размера n×n, тогда новая система уравнений состояния и наблюдения объекта имеет вид
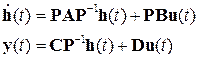
откуда следует, что матрицы коэффициентов новой системы равны Ah=PAP-1, Bh=PB, Ch=С P-1 (матрица D, при ее наличии, не претерпевает изменений, поскольку не связана с вектором состояний). Задаваясь произвольной матрицей Р необходимого размера, можно получить бесконечное множество описаний одной и той же системы в пространстве состояний. Однако при любых преобразованиях должны выполняться два важных условия:
- исходная и преобразованная система должны иметь одинаковые собственные значения (характеристические многочлены и их корни);
- преобразование базиса не меняет передаточную функцию системы.
Приведение к канонической управляемой форме: матрица преобразования в этом случае равна отношению матрицы управляемости новой системы к матрице управляемости исходной, т.е. P = QcQ-1. Необходимо найти характеристический полином системы, записать матрицы Ас и bс системы в канонической управляемой форме, вычислить матрицы управляемости обеих систем и по ним матрицу преобразования Р, с помощью которой осуществляется переход.
Переход к канонической наблюдаемой форме отличается лишь тем, что используются матрицы наблюдаемости, причем матрица преобразования базиса вычисляется по отношению матрицы наблюдаемости исходной системы к матрице наблюдаемости новой P = NN о-1 (обе матрицы составляются в виде столбца).
Для перехода к управляемой форме должна быть полностью наблюдаема пара (А, b), для перехода к наблюдаемой форме должна быть полностью наблюдаема пара (A, c).
Обратный переход, т.е. возвращение к исходной системе, например, после выбора параметров модального регулятора, во всех случаях осуществляется применением матрицы Р в обратном порядке, т.е. A = P-1AhP, B = P-1Bh, C = ChP, k = khP, где kh – матрица обратных связей замкнутой системы по переменным состояния.
К диагональной форме Ah = Λ приводятся системы с некратными вещественными полюсами, при этом матрицы исходной и преобразованной систем связаны соотношением A = TΛT-1 и матрица преобразования базиса равна P = T-1.
Пример 1. Пусть преобразуемый к канонической управляемой форме объект третьего порядка описывается системой уравнений
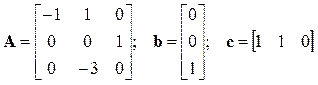 .
.
Характеристический полином объекта равен D ( s )= s 3 + s 2 +3s +3, матрица управляемости
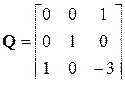 .
.
Используя вычисленный характеристический многочлен, записываем сопровождающую матрицу Ас, затем для пары (Ас, bc) найдем матрицу управляемости Q с новой системы и матрицу преобразования Р= QcQ -1
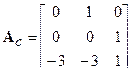 ;
; 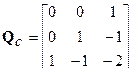 ;
; 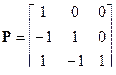 .
.
Применяя формулы Ас=РАР-1, bc=Pb, cc=cP-1, найдем описание системы в канонической форме управляемости (учитывая, что две матрицы были нам уже известны, оставалось вычислить лишь сс)
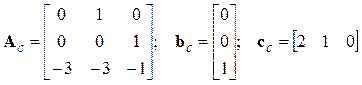 .
.
Задания для самостоятельного решения.
2.11.1 Восстановить исходное описание системы, если известны использованная матрица преобразования Р и новое описание
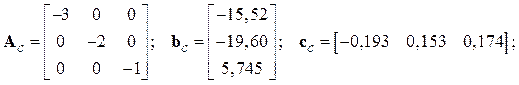
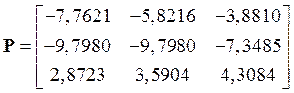
2.11.2 Перейти к канонической управляемой форме от системы
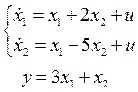
2.11.3 Перейти к канонической наблюдаемой форме от системы
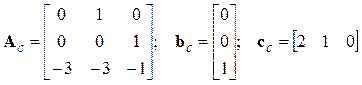
2.11.4 Перевести наблюдаемое представление в управляемое
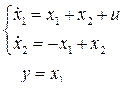
2.11.5 Перейти к канонической управляемой форме от системы
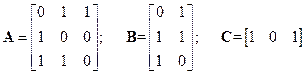
Ответы
1.1.1.2 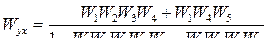 .
.
1.1.1.6 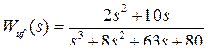 .
.
1.1.2.2 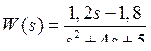 .
.
1.1.2.5 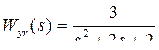 .
.
1.1.3.1 k(∞) = ∞.
1.1.3.5 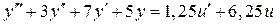 .
.
1.2.1.1  .
.
1.2.1.5  .
.
1.2.2.2 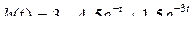 .
.
1.2.2.4 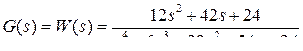 .
.
1.2.3.2 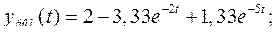
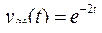 .
.
1.2.3.6  .
.
1.3.1.2 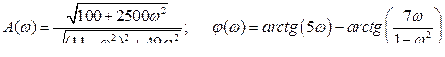 .
.
1.3.1.4 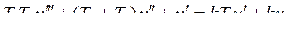 .
.
1.3.2.1 ωср,1 = 0,01 рад/с, ωср,2 = 100 рад/с.
1.3.2.4 –20 дБ/дек.
1.4.1.2 При остальных левых полюсах система имеет один полюс s = 0 и находится на апериодической границе устойчивости.
1.4.1.4 Частота незатухающих колебаний ωгран = 1,41 рад/с.
1.4.2.3 Система устойчива.
1.4.2.10 Система на колебательной границе устойчивости.
1.4.3.2 Предельное значение kc = k1k2k3 = 12,6.
1.4.3.5 Система неустойчива, имеет два правых корня (рисунок 3.1, а).
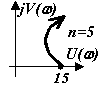
| 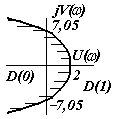
| 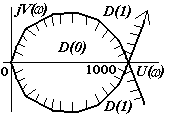
|
а б в
Рисунок 3.1
1.4.4.1 Система устойчива при k < 2 (риснок 3.1, б).
1.4.4.3 Система устойчива при 0 < k < 1000 (рисунок 3.1, в).
1.4.5.2 Запас по амплитуде АМ = 1, запас по фазе φМ = 180°.
1.4.5.9 Запас по амплитуде АМ = 1.
1.5.1.3 Перерегулирование σ = 0.
1.5.1.6 Перерегулирование σ = 0,7/1,05 = 0,667; коэффициент демпфирования ψ = (1,05 – 0,5)/(1,05 – 0) = 0,524; время регулирования на уровне Δ = 0,05×1,05 = 0,052 равно примерно 22 с.
1.5.2.6 Время регулирования tрег = 3/0,5 = 6 с; перерегулирование σ = exp(–π/3,88) = 0,445 или 44,5 %.
1.5.2.7 tрег = 0 с, σ = 0.
1.5.3.3 Время регулирования 0,314 < tрег < 1,256 с; перерегулирование σ = (1,18*3 + 0,277*2 – 3)/3 = 0,365 или 36,5 %.
1.5.3.5 Р(0) = 0,9 = h(∞), следовательно ε(∞) = 1 – 0,9 = 0,1.
1.5.4.1 J1 = k.
1.5.4.3 J1 = 1.
1.5.5.2 ε(∞) = 1 – 0,909 = 0,091 или 9,1 %.
1.5.5.4 С0 = 0, С1 = 1, С2 = -9.
2.1.2 k(∞) = ∞.
2.1.6 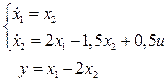 .
.
2.2.3 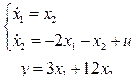 .
.
2.2.4 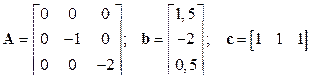 .
.
2.3.2 d = [10].
2.3.5 После подготовки схемы (рисунок 3.2) получаем систему уравнений
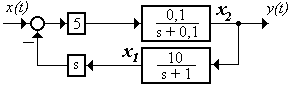
Рисунок 3.2
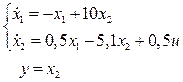
2.4.1 Схема на интеграторах (рисунок 3.3)
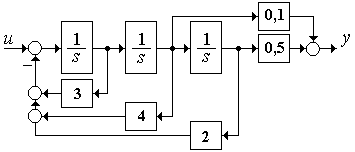
Рисунок 3.3
2.4.2 Построенная схема (рисунок 3.4)
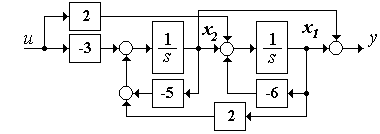
Рисунок 3.4
2.5.3 Присоединенную матрицу проще вычислить для системы с диагональной матрицей А
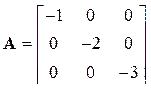 ;
;
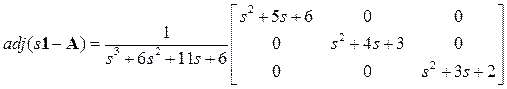 .
.
2.5.5 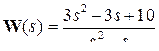 .
.
2.6.1 Реакция на начальные условия равна
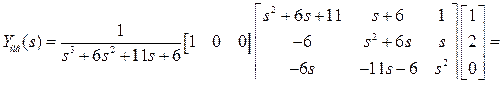
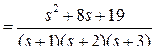 ;
;
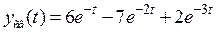 .
.
2.6.5 Система неустойчива, так как имеет правый полюс +3.
2.7.1 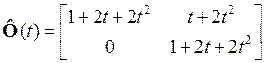 .
.
2.7.5 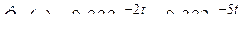 .
.
2.8.3 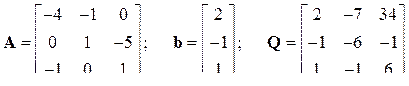 .
.
Система полностью управляема, так как ранг матрицы управляемости Q равен порядку системы n = 3.
2.8.7 Матрица наблюдаемости системы 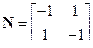 , ранг матрины N равен 1, поэтому система наблюдаема частично, порядок наблюдаемости равен 1.
, ранг матрины N равен 1, поэтому система наблюдаема частично, порядок наблюдаемости равен 1.
2.9.2 При заданных передаточной функции объекта и схеме наблюдателя величина К на значение отрицательного коэффициента 2 при s1 не влияет.
2.9.3 Схема наблюдателя приведена на рисунке 3.5.
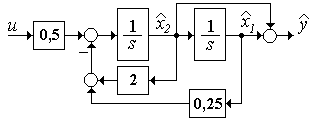
Рисунок 3.5
2.10.3 Исходя из показателей регулирования выбираем три действительных одинаковых корня – типовой полином Ньютона третьего порядка (Приложение Г) с величиной ω = tтаб/tзад = 6,3/3 = 2,1. Тогда желаемый вид полинома s3 + 6,3s2 + 13,23s + 9,26 обеспечит время регулирования 3 с и перерегулирование σ = 0. Приведенная передаточная функция объекта 3,125/(s3 + 0,25s2 + 2,5s + 0,625). По величине статизма выбираем коэффициент усиления регулятора, размещаемого вне контура обратных связей K = 0,98×9,26/3,125 = 2,9039.
Сравнивая общий вид желаемого характеристического полинома 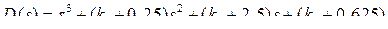 и его расчетный вид, находим значения коэффициентов обратных связей по переменным состояния k1 = 6,3 – 0,25 = 6,05; k2 = 13,23 – 2,5 = 10,73; k3 =
и его расчетный вид, находим значения коэффициентов обратных связей по переменным состояния k1 = 6,3 – 0,25 = 6,05; k2 = 13,23 – 2,5 = 10,73; k3 =
= 9,26 – 0,625 = 8,635 и общий вид структурной схемы замкнутой системы регулирования (рисунок 3.6).
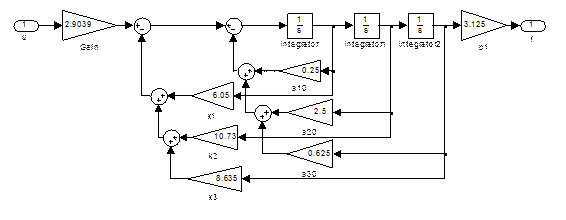
Рисунок 3.6
2.11.2 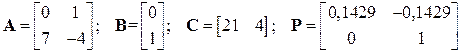 .
.
Литература
1 Бороденко В.А. Практический курс теории линейных систем автоматического регулирования : учеб. пособие. – Павлодар : Кереку, 2006. – 260 с.
2 Сборник задач по теории автоматического регулирования и управления / под ред. В.А. Бесекерского. – 5-е изд., перераб. – М. : Наука, 1978. – 512 с.
3 Топчеев Ю.И. Задачник по теории автоматического регулирования : учеб. пособие для вузов / Ю.И. Топчеев, А.П. Цыпляков. – М. : Машиностроение, 1977. – 592 с.
4 Задачник по теории автоматического управления / под общей ред. А.С. Шаталова. – М. : Энергия, 1971. – 496 с.
5 Французова Г.А. Сборник задач по теории автоматического управления : учебное пособие. Ч. 2. / Г.А. Французова, О.Я. Шпилевая, В.Д. Юркевич. – Новосибирск : Изд-во НГТУ, 2001. – 51 с.
6 Клавдиев А.А. Теория автоматического управления в примерах и задачах. Часть 1. Анализ линейных непрерывных систем автоматики : учебное пособие. – СПб. : СЗТУ, 2005. – 74 с.
7 Ким Д.П. Сборник задач по теории автоматического управления. Многомерные, нелинейные, оптимальные и адаптивные системы. – М. : Физматлит, 2008. – 328 с.
8 Мирошник И.В. Теория автоматического управления. Линейные системы. – СПб. : Питер, 2005. – 336 с.
Приложение А
(справочное)
Таблица соответствия оригиналов и изображений
Таблица А.1
| Изображение X(s) | Оригинал x(t) | |
| k e –τs | k∙1(t– τ ) запаздывание на τ > 0 | |
| | импульсная функция k ∙δ(t) | |
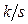
| – простой нулевой корень | скачок k∙1(t) или просто k |
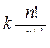
| – кратный нулевой корень | k ∙tn – степенной ряд от t |
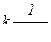
| – простой действительный корень | 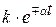 – экспонента – экспонента
|
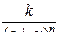
| – кратный действительный корень | 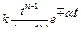 , при n > 1 , при n > 1
|
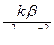
| – сопряженные мнимые корни | k∙sinβt – гармоническая функция |
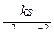
| – сопряженные мнимые корни | k∙cosβt – гармоническая функция |
|
| 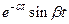 - затухающая
гармоническая функция - затухающая
гармоническая функция
| |
|
| 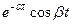 - затухающая
гармоническая функция - затухающая
гармоническая функция
| |
| сопряженные комплексные корни
с вычислением | а) предпочтительная форма
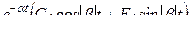 б) через синус (угол в радианах)
б) через синус (угол в радианах)
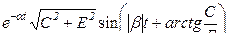 в) через косинус (угол в радианах)
в) через косинус (угол в радианах)
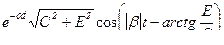
| |
| сопряженные комплексные корни (раздельное представление)
| 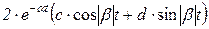 перед d ставят плюс, если знаки мнимых частей изображения в числителе и знаменателе совпадают (как показано), а иначе минус
перед d ставят плюс, если знаки мнимых частей изображения в числителе и знаменателе совпадают (как показано), а иначе минус
| |
Примечание – Даже если скачок 1(t) в формуле для входной функции не пишется, то всегда подразумевается, т.к. по Лапласу при t = 0- любая функция f( t) равна нулю, а затем она появляется скачком. Однако сомножитель 1/ s вводят в изображение входной функции лишь в том случае, если она представляет собой чисто ступенчатое воздействие, даже если в функциях-оригиналах другого вида скачок и был указан.
Приложение Б
(справочное)
Дата: 2019-02-19, просмотров: 781.
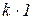
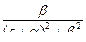
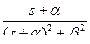
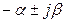 , объединенные в одну дробь
, объединенные в одну дробь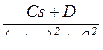 ,
,