Для управляемости системы необходимо и достаточно, чтобы матрица управляемости вида Q = [B| AB| A2B|…|An-1B] имела ранг, равный n. При управляемости системы говорят также, что пара (А, В) управляема.
Ранг матрицы (Rank) равен порядку её наибольшего ненулевого минора. Матрица Q составляется присоединением справа к матрице В произведения матриц АВ, затем произведения А(АВ) и т.д. Размерность матрицы Q равна (n × nr), где r – число входов. Если ранг матрицы B (обозначим его RB) не равен единице, то вычисление матрицы Q можно закончить досрочно по формуле Q=[B; AB; …; An-RbB].
Система полностью управляема при RankQ = n, полностью неуправляема при RankQ = 0, частично управляема при 0 < RankQ < n, порядок управляемости равен RankQ.
Для наблюдаемости системы необходимо и достаточно, чтобы матрица наблюдаемости N = [cT; ATcT; (AT)2сT; …; (AT)n-1cT] имела ранг, равный порядку системы n. Символ Т означает транспонирование или перевод вектора-строки в вектор-столбец. Говорят иначе, что пара (А, с) наблюдаема.
Система полностью наблюдаема при RankN = n, полностью ненаблюдаема при RankN = 0, частично наблюдаема при 0 < RankN < n, порядок наблюдаемости равен RankN.
Если ранг матрицы С (обозначим его RC) больше единицы, то число вычислений можно сократить, пользуясь формулой
N = [cT; ATcT; (AT)2сT; …; (AT)n-RccT].
Существует и иная форма составления матрицы наблюдаемости – по вертикали без транспонирования
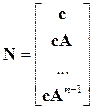 .
.
Если сокращены одинаковые нули и полюса, передаточная функция W(s) и матрица передаточных функций 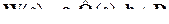 описывают только управляемую и наблюдаемую часть системы. Наличие сокращаемых пар нуль-полюс приводит к неуправляемости (ненаблюдаемости) системы. При диагональной матрице А уже можно говорить о неполной управляемости или наблюдаемости системы, если соответственно матрица b или c содержит нулевые элементы.
описывают только управляемую и наблюдаемую часть системы. Наличие сокращаемых пар нуль-полюс приводит к неуправляемости (ненаблюдаемости) системы. При диагональной матрице А уже можно говорить о неполной управляемости или наблюдаемости системы, если соответственно матрица b или c содержит нулевые элементы.
Пример 1. Оценить управляемость системы (достаточно иметь пару А и b).
Система: 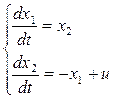 . Находим
. Находим 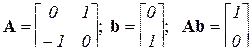 .
.
Определитель матрицы управляемости 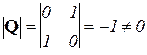 , следовательно, ранг матрицы равен двум, что равно порядку системы n = 2, система полностью управляема.
, следовательно, ранг матрицы равен двум, что равно порядку системы n = 2, система полностью управляема.
Задачу можно было не решать: числитель ПФ содержит только 1 (это видно из матрицы b), следовательно, сокращаемые пары нуль-полюс отсутствуют и система полностью управляема.
Пример 2. Оценить управляемость системы.
Система: 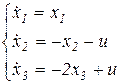
| Матрица А диагональная (в каждой строке одна переменная с возрастающим индексом). Уже ясно, что система неуправляема по x 1 (по полюсу +1), поскольку в первом уравнении нет u. Проверим вывод. |
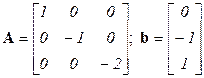 ;
; 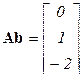 ;
; 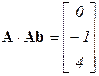
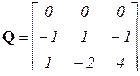 ; т.к.
; т.к. 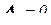 , а
, а  ,
,
то RankQ = 2 ≠ n = 3. Система частично управляема, порядок управляемости равен двум.
Пример 3. Оценить наблюдаемость системы
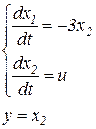 , записываем
, записываем 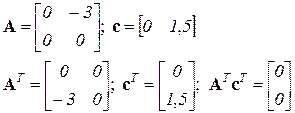
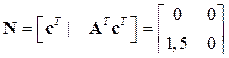 ; либо иначе
; либо иначе 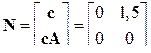 .
.
С учетом того, что Δ2 = 0; Δ1 = 1,5, делаем вывод, что RankN = 1 – система частично наблюдаема, порядок наблюдаемости равен 1.
Пример 4. Проверить управляемость системы 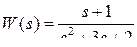 .
.
Передаточная функция W(s)=(s + 1)/(s + 1)/(s + 2) содержит сокращаемую пару (диполь) нуль -1/полюс -1, что ведет либо к неуправляемости, либо к ненаблюдаемости системы. От чего это будет зависеть? Составим описание системы в канонической управляемой форме и проверим управляемость
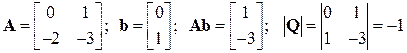 ; RankQ = 2.
; RankQ = 2.
Система в таком представлении полностью управляема (но не вполне наблюдаема). Составим описание системы в канонической наблюдаемой форме и снова проверим управляемость
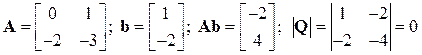 ; RankQ = 1.
; RankQ = 1.
А теперь система управляема частично. Таким образом, если в ПФ системы обнаруживается сокращаемая пара, неуправляемость или ненаблюдаемость зависит от того, какое представление выбирается для перехода в пространство состояний. Если же в ПФ сокращаемые пары отсутствуют, система полностью управляема и наблюдаема.
Задания для самостоятельного решения.
2.8.1 Проверить управляемость объекта 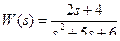 .
.
2.8.2 Проверить управляемость объекта
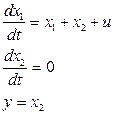
2.8.3 Проверить управляемость объекта
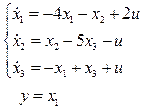
2.8.4 Проверить наблюдаемость объекта 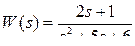 .
.
2.8.5 Проверить наблюдаемость объекта (рисунок 2.21)
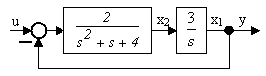
Рисунок 2.21
2.8.6 Проверить управляемость объекта
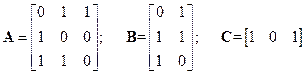 .
.
2.8.7 Оценить наблюдаемость системы
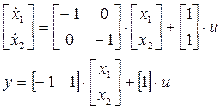
2.8.8 Оценить наблюдаемость системы
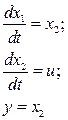
Наблюдатели состояния
Если не все переменные состояния объекта регулирования измеряются, либо имеют место существенные искажения (помехи), используют специальное оценивающее устройство – наблюдатель.
Наблюдатель в виде параллельного фильтра представляет собой модель объекта регулирования на интеграторах в каноническом управляемом представлении. Его вход подключается параллельно входу объекта регулирования, а с выходов интеграторов снимают идеальные значения переменных состояния объекта (оценки), которые обозначают значком «каре» ^ над символом переменной. Разница значений выходов объекта и наблюдателя называется невязкой (обозначается значком «тильда» ~ над символом сигнала), при совпадении модели с оригиналом невязка стремится к нулю.
Если объект управления неустойчив, либо требуется ускорить переходный процесс в наблюдателе, наблюдатель строят в виде фильтра Калмана. В нём сигнал невязки через компенсирующее звено или корректирующие обратные связи подается на вход наблюдателя вместе с обычным входным сигналом, и, если невязка не равна нулю, переходный процесс принудительно демпфируется.
Пример 1. Построить наблюдатель в виде параллельного фильтра к объекту с передаточной функцией W(s) = 3s/(2s2 + 4s + 1).
Модель объекта (описание наблюдателя) соответствует канонической форме управляемости
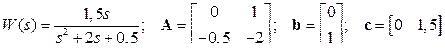 .
.
Этому описанию отвечает структурная схема (рисунок 2.22)
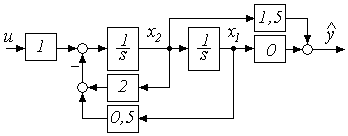
Рисунок 2.22
Пример 2. Построим наблюдатель в виде фильтра Калмана для объекта, заданного системой дифференциальных уравнений
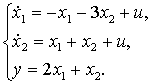
обеспечив показатели качества переходного процесса ошибки наблюдателя tрег = 1 с, σ = 30 %.
По матрицам коэффициентов объекта регулирования определяем его передаточную функцию (объект неустойчив)
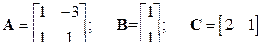
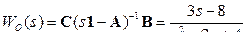 .
.
В фильтре Калмана второго порядка с дифференциальным уравнением р2 y + a 1 py + a 2 y = bu компенсирующая добавка образуется обратными связями с коэффициентами k1, k2 (рисунок 2.23).
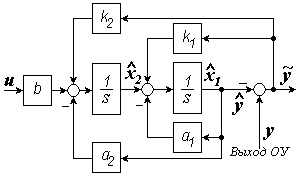
Рисунок 2.23
В соответствии с матрицей 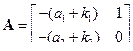 характеристический полином наблюдателя имеет вид D(s) = s2 +(a1 +k1)s + (a2 + k2) или D(s) = s2 +(–2 +k1)s + (4 + k2).
характеристический полином наблюдателя имеет вид D(s) = s2 +(a1 +k1)s + (a2 + k2) или D(s) = s2 +(–2 +k1)s + (4 + k2).
Исходя из требований к качеству переходного процесса наблюдателя модуль действительной части αmin корней его характеристического уравнения при Δ = 5 % должен быть не менее, чем 3/tрег = 3, тогда мнимая часть равна β = –παmin/ln(σ) = –3,1415926*3/ln(0,3) = 7,83. По двум выбранным корням –3 ± j7,83 определяем вид желаемого устойчивого характеристического полинома 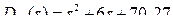 .
.
Из равенства D(s) = Dж(s) находим неизвестные коэффициенты корректирующих обратных связей k1 = 6 + 2 = 8, k2 = 70,27 – 4 = 66,27.
Пример 3. Рассчитать параметры наблюдателя в виде фильтра Калмана (рисунок 2.24) с компенсирующим звеном, имеющим передаточную функцию L(s) = k(τ1s + 1)/(τ2s + 1), при тех же требованиях к качеству переходного процесса наблюдателя и параметрах ПФ модели объекта регулирования Wo(s).
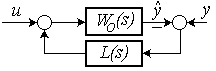
Рисунок 2.24
Передаточная функция модели объекта регулирования равна
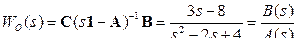 ,
,
а характеристическое уравнение наблюдателя имеет вид
 ,
,
откуда, приравняв числитель нулю и нормируя, получаем
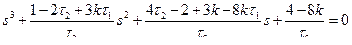 .
.
Желаемый характеристический полином третьего порядка формируем из корней с одинаковой действительной частью –3 ± j7,83 и
–3, он равен Dж(s) = s3 + 9s2 + 88s + 211. Приравнивая D(s) = Dж(s), находим неизвестные коэффициенты k, τ1 и τ2.
Задания для самостоятельного решения.
2.9.1 Определить значение L(s) = K из условия требуемой относительной статической ошибки наблюдателя Su = 0,02 при значениях свободных членов передаточной функции модели b m = 10; an = 4.
2.9.2 Определить значение L(s) = K из условия устойчивости наблюдателя, если ПФ объекта равна Wo(s) = 3/(s2 – 2s + 2).
2.9.3 Рассчитать параметры и построить структурную схему наблюдателя состояния для объекта регулирования с передаточной функцией W(s) = 2(s + 1)/(4s2 + 8s + 1).
2.9.4 При требованиях к качеству переходного процесса ошибки наблюдения tрег = 6 с; σ = 15 % разработать наблюдатель состояния для объекта регулирования, описываемого уравнениями
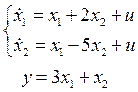
2.9.5 Разработать наблюдатель состояния с качеством переходного процесса ошибки наблюдения tрег = 5 с; σ = 30 % для объекта регулирования, описываемого ПФ W(s) = (2s + 1)/(s2 + 1).
2.9.6 При качестве переходного процесса ошибки наблюдения tрег = 12 с; σ = 15 % создать наблюдатель для объекта регулирования
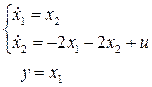
Дата: 2019-02-19, просмотров: 740.