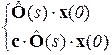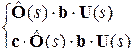На структурной схеме переменные состояния могут быть назначены разным образом, поэтому и описания системы в пространстве состояний будут отличаться. Все матрицы имеют нестандартный вид. Однако переменная всегда назначается на выходе блока с s в знаменателе, а ОДУ первого порядка для каждого такого блока записывают в зависимости от вида знаменателя:
а) звено с нулевым корнем в знаменателе (рисунок 2.3, а)
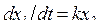или 
;
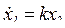б) звено с действительным корнем, две формы (рисунок 2.3, б)
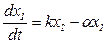или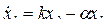 
; 
.
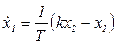Правая часть после нормирования равна произведению входа на числитель минус произведение выхода на коэффициент знаменателя.
| 
| 
|
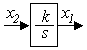
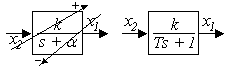
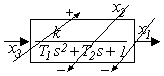
а б в
Рисунок 2.3
Звено c комплексными сопряженными корнями (рисунок 2.3, в), не разлагается на два простых, поэтому вводят условно переменную состояния с промежуточным индексом и составляют два уравнения
.
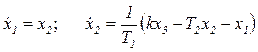Эта запись соответствует переходу от дифференциального уравнения к канонической форме наблюдаемости с нормированием по старшему коэффициенту знаменателя
.
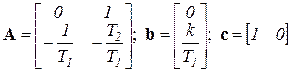Любой блок порядка n>1 может быть описан с использованием канонической наблюдаемой формы без его разложения на простые звенья. В особенности это важно, если блок имеет нули, т.е. порядок многочлена числителя его передаточной функции не ниже единицы.
→ 
.
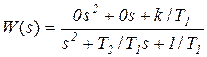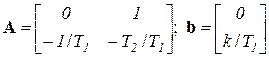Умножая матрицу А на вектор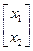 
и вектор b на вход x3, получаем систему уравнений, которую затем совмещаем с уравнениями оставшейся части структурной схемы.
Поскольку в пространстве состояний не могут быть отдельно описаны дифференцирующие и форсирующие звенья с m > n, то, получив в правой части уравнения дополнительную производную с индексом, меньшим текущего номера уравнения, ее пробуют выразить через значение, полученное ранее, в предыдущих дифференциальных уравнениях. Обычно это имеет место при обратных связях через s.
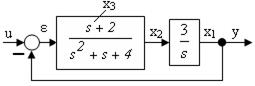
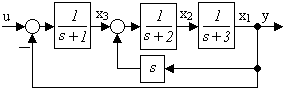
Пример 1. Описать систему (рисунок 2.4, а)
| 
|
а б
Рисунок 2.4
Сначала рассматриваем сложный блок с переменной s в числителе, учитывая, что вектор с для него составлен единственной единицей и в вычислениях не нуждается, а переменная состояния на выходе блока имеет индекс 2:
→ 
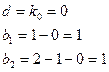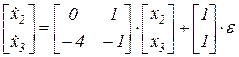
Затем описываем всю систему, включая в нее этот блок:
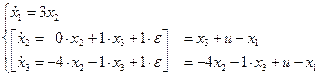
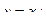
и окончательно
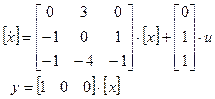
Пример 2. Составляя уравнения состояния для случая, когда в цепи обратной связи есть звено дифференцирования с s (рисунок 2.4, б) учитываем, что умножение на s в операторной области соответствует взятию производной во временной области.
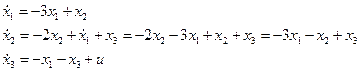
Поскольку в правой части уравнений производных быть не должно, вместо производной подставляется ее значение, вычисленное ранее. Окончательно
.
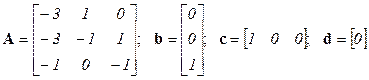Задания для самостоятельного решения.
2.3.1 По структурной схеме (рисунок 2.5) составить полное описание системы в пространстве состояний матрицами А, b, c и d
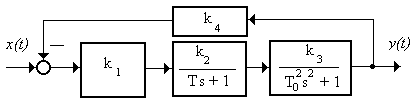
Рисунок 2.5
2.3.2 Найти, чему равна матрица d системы (рисунок 2.6)
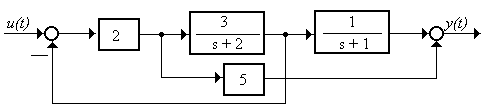
Рисунок 2.6
2.3.3 Описать переменными состояния систему (рисунок 2.7)
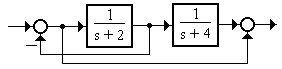
Рисунок 2.7
2.3.4 Описать переменными состояния систему (рисунок 2.8)
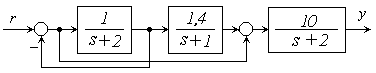
Рисунок 2.8
2.3.5 Описать переменными состояния систему (рисунок 2.9)
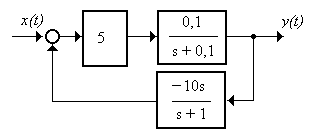
Рисунок 2.9
2.3.6 Описать переменными состояния систему (рисунок 2.10)
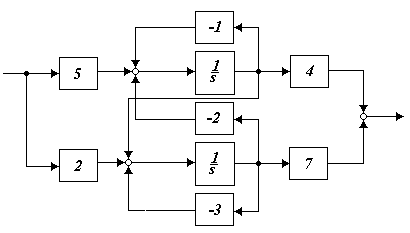
Рисунок 2.10
Синтез структурной схемы
Независимо от реальной конструкции, система в пространстве состояний может быть представлена набором интеграторов (звеньев 1/s, осуществляющих операцию интегрирования входной величины по времени), сумматоров и блоков, воспроизводящих коэффициенты усиления в собственных и перекрестных связях.
Пример 1. Перейдем от матриц A, b, c, d
.
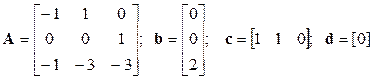к структурной схеме (рисунок 2.11), для чего выбираем число звеньев (равно порядку матрицы А), определяем корни знаменателей ПФ по диагональным элементам матрицы А (s = -1 у блока с переменной х1 на выходе и s = -3 у блока с переменной х3), находим коэффициенты прямых связей – числители ПФ блоков между х2 и х1, между х3 и х2 (оба числителя равны 1). В схеме имеются две отрицательные обратные связи: единичная ООС от х1 к х3 и с коэффициентом 3 от х2 к х3. На входе системы находится блок с коэффициентом 2, выход y связан с системой через коэффициенты 1 матрицы с.
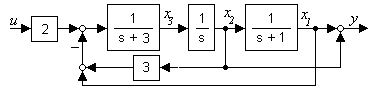
Рисунок 2.11
Пример 2. Построить структурную схему объекта, заданного системой дифференциальных уравнений
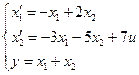
Порядок объекта равен двум, используем два интегратора с сумматором на входе каждого. Назначаем переменные на выходах интеграторов, двигаясь от выхода схемы ко входу, значения всех производных формируются на входе интеграторов. Проводим связи на входы сумматоров в соответствии с видом уравнений. Например, производная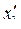 
образуется на входе последнего интегратора суммированием выходной переменной х1 (с минусом) и переменной х2, взятой с коэффициентом 2 (смотри первую строку системы дифференциальных уравнений). Сумматор на выходе необходим для образования выходной величины из переменных состояния, взятых с соответствующими коэффициентами y = x1 + x2 (рисунок 2.12).
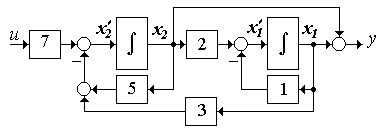
Рисунок 2.12
Пример 3. Построить структурную схему объекта по дифференциальному уравнению 
.
Поскольку порядок системы равен трем, используем три интегратора 1/s, включив их последовательно и установив сумматор на входе первого интегратора слева. К инвертирующему входу этого сумматора подключаем через согласующие сумматоры блоки с коэффициентами (по порядку): а1 – с выхода первого интегратора, а2 – с выхода второго интегратора, а3 – с выхода третьего интегратора.
Если в правой части дифференциального уравнения нет производных, блок с коэффициентом b помещаем на входе главного сумматора (рисунок 2.13), в ином случае необходим еще один сумматор на выходе схемы, к которому через блоки с коэффициентами b0-bn подключают выходы интеграторов.
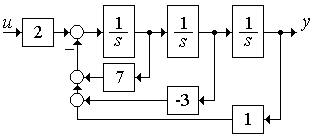
Рисунок 2.13
Задания для самостоятельного решения.
2.4.1 Перейти к структурной схеме от дифференциального уравнения объекта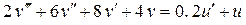 
.
2.4.2 Изобразить структурную схему системы по уравнениям состояния
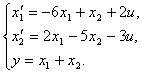
2.4.3 Построить структурную схему на интеграторах
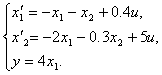
2.4.4 Составить структурную схему системы (рисунок 2.14), используя разложение ПФ на простые дроби
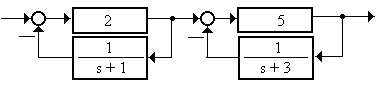
Рисунок 2.14
2.4.5 Составить структурную схему объекта по известной ПФ
.
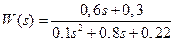Основные матричные функции
(s1 – A) – характеристическая матрица, аналог характеристического полинома одномерной системы D(s).
Ф(s) = (s1 – A)-1 – системная матрица (резольвента), называемая также передаточной матрицей или матрицей передаточных функций (МПФ) для переменных состояния, аналог системной функции 1/D(s).
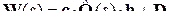– реальная МПФ для назначенных входов и выходов (передаточная матрица выходов), совпадает по виду с Ф(s) только в частном случае.
Пример 1. Система задана в пространстве состояний матрицами
.
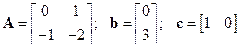Характеристическая матрица
.
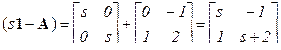Характеристический полином (определитель характеристической матрицы)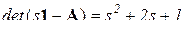 
.
Присоединенная матрица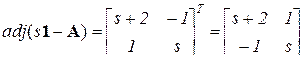 
.
Алгоритм вычисления присоединенной матрицы: каждый элемент исходной матрицы (s1 – A) заменяют его алгебраическим дополнением и полученная матрица транспонируется (приложение В).
Резольвента
,
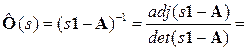
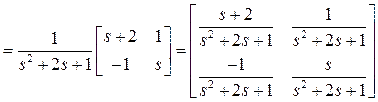матрица передаточных функций выходов
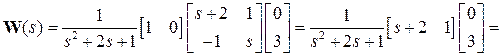
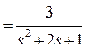
Задания для самостоятельного решения.
2.5.1 Найти индивидуальную передаточную функцию W13(s), переведя в пространство состояний систему
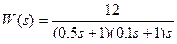
2.5.2 От структурной схемы (рисунок 2.15) перейти классическим методом к описанию системы в пространстве состояний системной матрицей Ф(s)
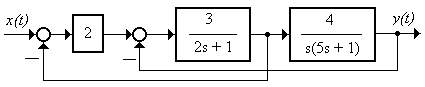
Рисунок 2.15
2.5.3 Вычислить присоединенную матрицу (k = 3,4) системы (рисунок 2.16)
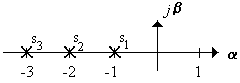
Рисунок 2.16
2.5.4 От структурной схемы (рисунок 2.17) перейти к описанию системы в переменных состояния, вычислить передаточную матрицу выходов
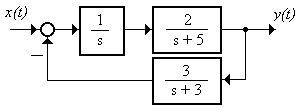
Рисунок 2.17
2.5.5 Определить матрицу W(s)
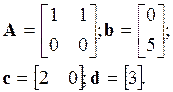
2.5.6 Найти характеристическую матрицу системы (рисунок 2.18)
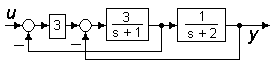
Рисунок 2.18
2.5.7 Определить реальную передаточную матрицу
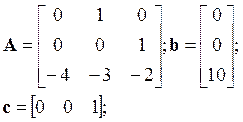
2.5.8 Найти системную матрицу объекта (рисунок 2.19)
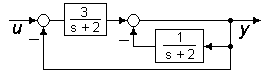
Рисунок 2.19
Решение уравнения движения
Решение дифференциального уравнения для переменных состояния x(t), т.е. изменение вектора состояния при известном векторе управления и начальных условиях (внутри системы), в общем виде
.
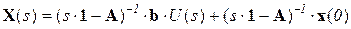Реакция на выходе системы вычисляется с учетом матрицы с
.
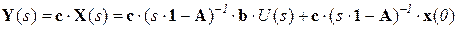| Свободная составляющая |
| – внутри системы, |
| – на ее выходах. | ||
| Вынужденная составляющая |
| – внутри системы, |
| – на ее выходах. |
Если система задана в наблюдаемой форме с упрощенной матрицей с, вместо вектора начальных значений переменных состояния х(0) может непосредственно использоваться вектор y(0) начальных значений рассогласования, скорости, ускорения и т. п. на выходе системы. В ином случае необходимо преобразование y(0) в х(0) с учетом коэффициентов матрицы с.
Матрицы, элементами которых являются весовые gij ( t ) или переходные hij ( t ) функции объекта, называются соответственно весовой (импульсной) g(t) и переходной h(t) матрицами. Их изображения определяют обычным способом.
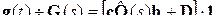– весовая матрица,
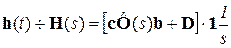– переходная матрица.
Пример 1. Найти при u( t ) = δ( t ) и начальных условиях y(0) = 1;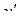 
(0) = -1 уравнения движения системы
.
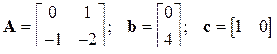Система задана в наблюдаемой форме с матрицей с = [1 0], поэтому вектор начальных значений переменных формируем по выходу
.
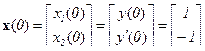Характеристическая матрица
.
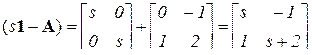Характеристический полином (определитель характеристической матрицы)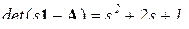 
.
Резольвента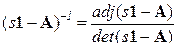 
, где присоединенная матрица
.
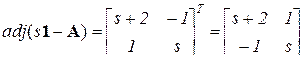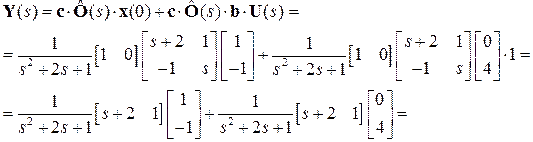
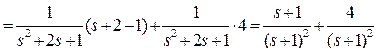
Заменяем по таблице соответствия изображения на оригиналы
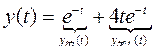
Пример 2. Найти изображение реакции на f(t) = 3e–t системы
.
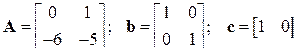Изображение входного воздействия F(s) = 3/(s+1).
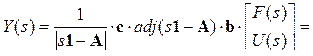
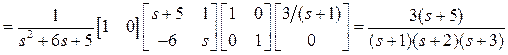
Задания для самостоятельного решения.
2.6.1 Найти свободную составляющую переходного процесса системы
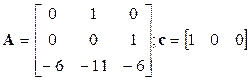
при начальных условиях x1(0) = 1, x2(0) = 2, x3(0) = 0 и собственных значениях s1 = -1, s2 = -2, s3 = -3 матрицы А.
2.6.2 При воздействиях u(t) = 1(t) и f(t) = 3(t) найти реакцию y(t) системы
.
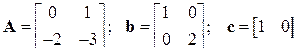2.6.3 Найти переходную функцию для переменных состояния x( t ) системы
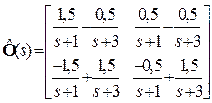
2.6.4 Рассчитать весовую матрицу системы (рисунок 2.20) при значениях параметров k1 = 1, k2 = 12, T1 = 1, T2 = 0,1.
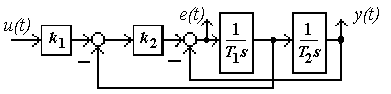
Рисунок 2.20
2.6.5 Оценить устойчивость системы, если
.
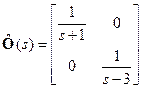Дата: 2019-02-19, просмотров: 560.
