Поскольку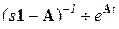 
, то фундаментальную матрицу Ф(t) определяют как матричную экспоненту от A∙t тремя способами:
а) разложением в бесконечный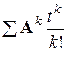 
или конечный ряд
,
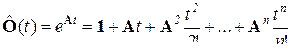где n – порядок системы.
Точность расчета снижается из-за конечного числа членов ряда. Способ полезен в случаях, когда невозможно найти корни характеристического уравнения системы, либо производится расчет для конкретного момента времени t.
б) по формуле Сильвестра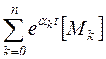 
, где αk – собственные значения матрицы А (корни характеристического уравнения системы), или в развернутом виде
.
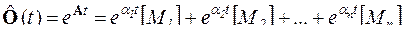Здесь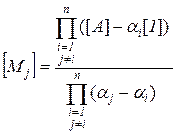 
| – все разности для других корней, – все разности этого корня с другими. |
Особенности метода – коэффициенты сразу получаются в матричном виде, но обязательно нужно знать корни характеристического уравнения. Приведенная формула пригодна для простых действительных корней характеристического уравнения, для кратных корней используется более сложная формула.
в) Наконец, Ф(t) вычисляется и как обратное преобразование Лапласа от системной матрицы Ф(s), или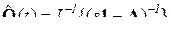 
.
Здесь также нужно обязательно знать корни, требуется многократное поэлементное преобразование, но зато способ пригоден для любых корней (комплексных, кратных, простых).
Пример 1. Определим матричную экспоненту для системы с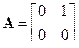 
. Поскольку уже при k = 2 получена нулевая матрица
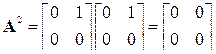
расчет далее можно не продолжать и результат записывается в виде
.
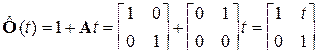Пример 2. Определить Ф(t) методом Сильвестра для системы
.
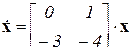Вычисляем характеристический полином, находим его корни
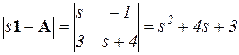; s1 = –1; s2 = –3.
Вычисляем матрицы коэффициентов при собственных модах системы
;
;
.
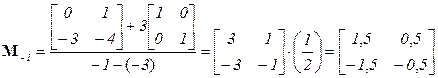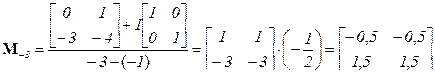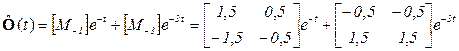Пример 3. Определить с помощью обратного преобразования Лапласа фундаментальную матрицу системы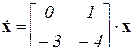 
.
Находим корни характеристического полинома и адъюнкту
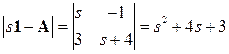; s1 = –1; s2 = –3.
; 
.
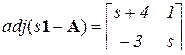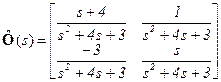Общий вид разложения на простые дроби
.
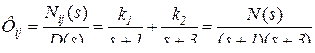Находим коэффициенты числителей простых дробей:
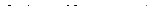k 1 = 1,5; k 2 = -0,5
k 1 = 0,5; k 2 = -0,5
k 1 = -1,5; k 2 = 1,5
k 1 = -0,5; k 2 = 1,5,
откуда получаем вид системной и фундаментальной матриц
;
.
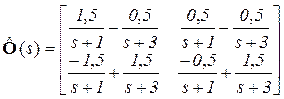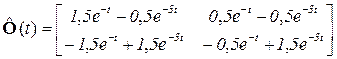Найдем, например, реакцию на начальные условия х1(0) = 2, х2(0) = 0 данной системы по известной Ф(t), если с=[1 0].
.
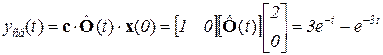Задания для самостоятельного решения.
2.7.1 Вычислить функцию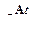 
, если матрица А системы равна
,
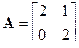2.7.2 Вычислить фундаментальную матрицу системы
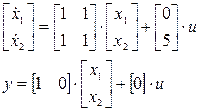
2.7.3 Найти матрицу Ф(s) для системы с функцией
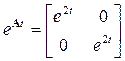
2.7.4 Найти реакцию на начальные условия х1(0) = -1, х2(0) = 0, используя матричную экспоненту Ф(t).
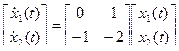
2.7.5 Записать реакцию Ф12(t) для системы
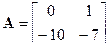
2.7.6 Рассчитать фундаментальную матрицу методом Сильвестра
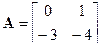
Дата: 2019-02-19, просмотров: 487.
