При описании системы переменными состояния дифференциальному уравнению n-го порядка a 0 y ( n ) + a 1 y ( n -1) + … + any = b 0 u соответствует система n дифференциальных уравнений первого порядка в нормальной форме Коши, разрешенных относительно производной.
Для перехода от ОДУ по методу фазовых переменных за первую переменную состояния принимают выходную величину, за остальные переменные состояния принимают n–1 производную выходной величины. Обязательно сначала нужно нормировать дифференциальное уравнение, т.е. делить обе части уравнения на коэффициент а0 ≠ 1 при старшей производной выходной функции (на старший коэффициент многочлена знаменателя передаточной функции).
Если порядок m ≠ 0 многочлена числителя ПФ меньше порядка n многочлена знаменателя, общий коэффициент ПФ (коэффициент перед правой частью ОДУ) записывается в уравнение для старшей переменной состояния, а коэффициенты многочлена числителя – в обратном порядке в уравнение выхода.
По системе уравнений составляется матрица состояния А (из коэффициентов при х) и матрица входа В (из коэффициентов при входном воздействии u), по уравнению выхода составляется матрица выхода С (из коэффициентов при х)
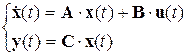
Сопровождающая матрица А (матрица Фробениуса) может быть записана прямо по ОДУ (по характеристическому полиному системы)
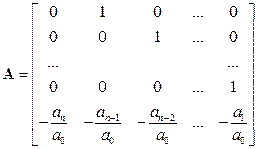 .
.
По уравнениям состояния или матрицам A, b, c указанного вида легко восстановить ПФ или ОДУ, учитывая, что в последней строке сопровождающей матрицы А записаны с конца, с обратным знаком коэффициенты нормированного характеристического многочлена, а в матрице c – коэффициенты многочлена числителя передаточной функции в обратном порядке.
Пример 1. Дифференциальное уравнение объекта управления 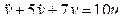 . Выбираем переменные состояния
. Выбираем переменные состояния 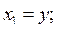
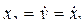 . В нормировании нет необходимости. Записываем для каждой из переменных состояния дифференциальное уравнение первого порядка, добавляем общее алгебраическое уравнение выхода
. В нормировании нет необходимости. Записываем для каждой из переменных состояния дифференциальное уравнение первого порядка, добавляем общее алгебраическое уравнение выхода
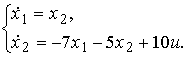
y = x 1
Пример 2. Пусть модель объекта управления имеет вид 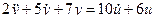 , тогда после нормирования (деления на 2), считая общий коэффициент перед правой частью уравнения равным единице, получим описание системы в пространстве состояний матрицами
, тогда после нормирования (деления на 2), считая общий коэффициент перед правой частью уравнения равным единице, получим описание системы в пространстве состояний матрицами
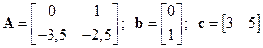 .
.
Задания для самостоятельного решения.
2.1.1 Записать передаточную функцию объекта регулирования, представленного в пространстве состояний моделью
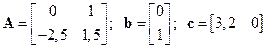
2.1.2 Определить коэффициент усиления в установившемся режиме
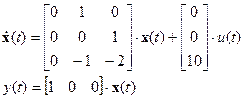
2.1.3 Записать матрицы коэффициентов A, B, C для системы
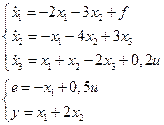
2.1.4 Составить уравнения состояния и выхода по дифференциальному уравнению объекта регулирования 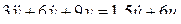 .
.
2.1.5 Определить матрицы А, b, c по дифференциальному уравнению объекта регулирования 0,5y(3) + y(2) + 2y(1) + 4y = 3u(2) +5u.
2.1.6 По модели объекта 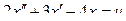 ,
, 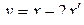 записать уравнения состояния и наблюдения.
записать уравнения состояния и наблюдения.
Канонические представления
Стандартные формы описания систем в пространстве состояний с сопровождающей матрицей А называются каноническими. Это каноническая управляемая форма (с упрощенной матрицей b) и каноническая наблюдаемая форма (с упрощенной матрицей с).
При m = n, т.е. одинаковых степенях полиномов числителя и знаменателя ПФ, появляется ненулевая матрица обхода d, которая содержит коэффициенты при входных воздействиях в уравнении выхода. Если матрица d нулевая, её можно не писать.
Пусть 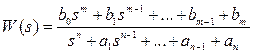 , m = n, тогда вычисления для перехода к канонической управляемой форме имеют вид
, m = n, тогда вычисления для перехода к канонической управляемой форме имеют вид
d = b0; c1 = bm - an∙d; c2 = bm-1 – an-1∙d … и т.п.
При d = b 0 = 0 (m < n) в матрицу с просто записываются коэффициенты числителя передаточной функции, начиная со свободного члена.
Другой способ перехода к канонической управляемой форме: нужно разделить числитель ПФ на ее знаменатель, получившееся отдельно стоящее слагаемое (частное) поместить в матрицу d, а коэффициенты числителя полученной рациональной дроби (остатка) записать в матрицу с как обычно, начиная со свободного члена.
Порядок расчета элементов матриц b и d для перехода к канонической наблюдаемой форме (в этом случае элементы матрицы b необходимо вычислять даже при нулевой матрице d, т.е. при m < n).
Пусть 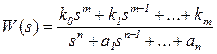 , m = n, тогда
, m = n, тогда
D = k 0 = b 0 ,
b1 = k1 – b0a1,
b2 = k2 – b0a2 – b1a1,
b 3 = k 3 – b 0 a 3 – b 1 a 2 – b 2 a 1 …
К стандартным формам относится также описание с диагональной (модальной) матрицей А, когда по главной диагонали матрицы записывают её собственные значения (корни характеристического уравнения). К описанию с диагональной матрицей А переходят путем разложения исходного выражения на простые дроби.
Если матрица А не сопровождающая, а произвольного вида, ее характеристический многочлен нужно вычислять как определитель 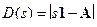 , где s – комплексная переменная Лапласа, 1 – единичная матрица.
, где s – комплексная переменная Лапласа, 1 – единичная матрица.
Корни характеристического уравнения 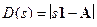 = 0 являются собственными значениями матрицы А. Матрицы подобны, если имеют одинаковые собственные значения (характеристические многочлены и их корни).
= 0 являются собственными значениями матрицы А. Матрицы подобны, если имеют одинаковые собственные значения (характеристические многочлены и их корни).
Многомерная система устойчива, если все собственные значения матрицы состояний А имеют отрицательную действительную часть, иначе – все корни характеристического полинома являются левыми. Вычислив характеристическое уравнение системы 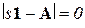 , можно оценить ее устойчивость любым из известных способов.
, можно оценить ее устойчивость любым из известных способов.
Пример 1. Передаточная функция объекта 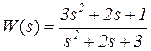 .
.
Каноническое управляемое представление (нормирование по a 0 не требуется, матрица b имеет стандартный вид, всегда одинаковый)
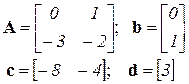
| где | d = b0 = 3, c1 = b2 – a2d = 1 – 9 = -8, c2 = b1 – a1d = 2 – 6 = -4. |
Пример 2. По уравнению y (3) + 2 y (2) + 3 y (1) + 4 y = 5 u (1) + 6 u составим каноническую наблюдаемую форму. Нормирование по старшему коэффициенту знаменателя при sn не требуется, так как он уже равен единице, многочлен числителя ПФ дополняем коэффициентами до той же степени, что и многочлен знаменателя
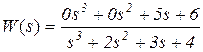 ,
, 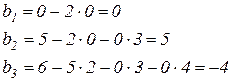
матрица d нулевая, поскольку m < n, и окончательно (матрица с имеет стандартный вид, всегда одинаковый)
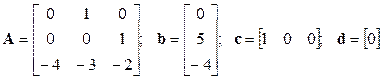 .
.
Пример 3. Перейти к переменным состояния разложением на простые дроби заданной передаточной функции
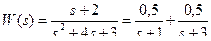 .
.
Коэффициенты на главной диагонали матрицы А равны её собственным значениям (полюсам системы) s1 = -1, s2 = -3; структурная схема соответствует рисунку 2.1. Матрицы b и с включены последовательно, поэтому, если вычеты 0,5 и 0,5 вписаны в матрицу b (как показано), то в матрицу с записываются единицы, и наоборот.
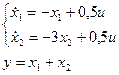 или или 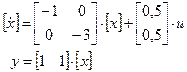
| 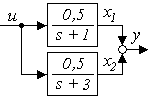 Рисунок 2.1
Рисунок 2.1
|
Пример 4. Оценить устойчивость системы, проверить подобие матрицы А и матрицы АА
Система 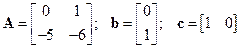 , матрица
, матрица 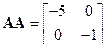 .
.
Характеристическая матрица
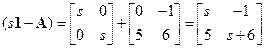 .
.
Характеристический многочлен (определитель характеристической матрицы) 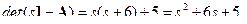 . По критерию Гурвица система устойчива, т.к. все коэффициенты характеристического многочлена положительны.
. По критерию Гурвица система устойчива, т.к. все коэффициенты характеристического многочлена положительны.
Характеристический многочлен матрицы 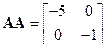 равен
равен 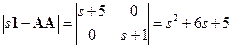 . Матрицы А и АА подобны, поскольку равны их характеристические многочлены.
. Матрицы А и АА подобны, поскольку равны их характеристические многочлены.
Задания для самостоятельного решения.
2.2.1 Оценить устойчивость системы
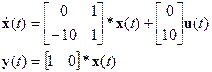
2.2.2 Описать в пространстве состояний каноническим наблюдаемым представлением, найдя передаточную функцию (рисунок 2.2)
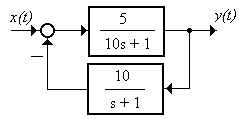
Рисунок 2.2
2.2.3 Описать каноническим управляемым представлением систему
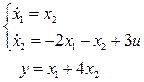
2.2.4 Описать в пространстве состояний с диагональной матрицей А объект, имеющий передаточную функцию
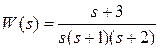 .
.
2.2.5 Представить канонической наблюдаемой формой систему 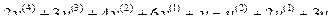 .
.
Дата: 2019-02-19, просмотров: 2038.