Основой геометрического представления сигналов служит тот факт, что совокупность чисел х1, х2, ... , хn, независимо от их происхождения, всегда может рассматриваться как совокупность координат точки в n-мерном пространстве, т.е. соответствующий вектор в n-мерном пространстве определяется совокупностью п чисел, которые являются его проекциями на соответствующие оси. Это записывается следующим образом:

Сигнал с ограниченным спектром, согласно теореме Котельникова, полностью задается дискретным множеством равноотстоящих отсчетов. Совокупность чисел, характеризующих значение функций отсчета в соответствующих точках, можно рассматривать как совокупность координат некоторой точки; таким образом, сигнал также представляется как вектор (точка) в многомерном пространстве, которое можно назвать пространством сигналов. Размерность пространства сигналов равна числу степеней свободы рассматриваемого сигнала. Как отмечалось выше, оценкой числа степеней свободы отрезка сигнала длительностью Т и ограниченной шириной F спектра является число 2FT.
В большинстве практических случаев число измерений пространства сигналов очень велико. Хотя такие пространства не допускают наглядного изображения, аналитические соотношения геометрии значительно облегчают рассмотрение проблем связи.
Расстояния в пространстве сигналов имеют наглядный смысл. Для так называемого евклидова пространства справедливо следующее соотношение для длины вектора:

| (3.54) |
которое является обобщением обычной теоремы Пифагора. В n-мерном пространстве длина вектора называется его нормой. Если рассмотреть два вектора x1 и х2 (на Рис. 3.6 показана двумерная модель), то можно найти угол между ними и расстояние между концами векторов.
 |
Рис. 3.6. Двумерная модель векторного пространства
Исходя из Рис. 3.6 получаем:
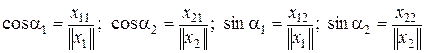 .
.
Тогда
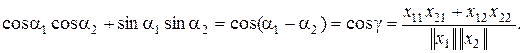
Обобщая полученное выражение на n-мерное пространство, можем записать
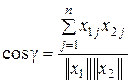
| (3.55) |
Для расстояния d между концами векторов будем иметь
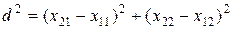
или для n-мерного случая

| (3.56) |
Для энергии Ec сигнала, представленного отсчетами, получено выражение
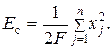
| (3.57) |
Сравнивая значение энергии с соотношением (3.57), можем записать ||х||2 = 2FEс.
Так как длительность сигнала конечна, то можно определить среднюю мощность сигнала Рс следующим образом: Pс = Eс /T. Тогда
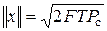
| (3.58) |
Итак, норма вектора сигнала (т. е. длина вектора) при заданной длительности и ширине спектра сигнала определяется его средней мощностью. Для стационарного случайного сигнала операция осреднения квадрата реализации по времени определяет дисперсию процесса, следовательно, норма вектора сигнала будет пропорциональна его среднему квадратическому значению
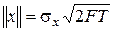
| (3.59) |
Простое геометрическое толкование имеют различные операции над сигналами. Например, если сигнал в канале искажается определенным образом, то пространство сигналов искривляется за счет определенного смещения каждой точки. Пропусканию сигнала через фильтр с полосой, меньшей ширины спектра, соответствует проектирование точки сигнала на некоторое подпространство, так как такая фильтрация уменьшает число степеней свободы сигнала. Наконец, сложение сигнала с помехой означает смещение точки сигнала на величину, пропорциональную среднеквадратическому значению помехи. Если помеха носит случайный характер, то она образует некоторую область неопределенности около каждой точки пространства сигналов.
Геометрическая модель позволяет дать наглядное изображение процессов, происходящих в линиях связи.
Контрольные вопросы
1. Дайте определение детерминированного и случайного процессов. Приведите примеры.
2. Дайте определение дельта-функции и укажите основные ее свойства.
3. Поясните смысл величин, входящих в тригонометрическую и комплкексную формы записи ряда Фурье.
4. Какой вид имеет спектр периодического сигнала?
5. Дайте определение понятий реализации и ансамбля реализаций случайного процесса.
6. Дайте определение основных характеристик случайного процесса.
7. Как описываются статистические свойства дискретных сообщений? Какие процессы называются марковскими?
8. Что такое «белый шум»? Каковы его свойства?
9. Каким образом оценивается в технике практическая ширина спектра сигнала, и какие характеристики полностью определяют сигнал?
10. Дайте геометрическое определение различимости сигналов.
Дата: 2019-02-24, просмотров: 331.