Достаточно широкий класс реальных сигналов охватывается их моделью в виде марковского процесса. Положим сложный сигнал строится из некоторого дискретного множества элементарных сигналов. Если источник генерирует в данный момент j-й элементарный сигнал, то говорят, что он находится в j-м состоянии. Полное описание процесса заключается в задании набора элементарных сигналов (состояний) {e_j} и условных вероятностей p_jk перехода источника из состояния j в состояние k.

Для полноты модели в рассмотрение можно включить случай, когда вероятность перехода p_jk зависит от времени пребывания источника в состоянии j: вероятность перехода в состояние k в интервале (t, t + dt) после перехода в состояние j равна p_jk(t)dt.

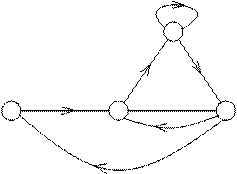
Этот сложный процесс может быть отражен очень простой графической моделью. Способ построения модели заключается в следующем. Состояниям источника ставятся в соответствие точки (узлы); возможность перехода из данного состояния в другое отображается наличием линии (ветви), соединяющей соответствующие узлы; направление перехода указывается стрелкой; вероятность перехода указывается числом около надлежащей ветви. Величины подчиняются очевидному соотношению 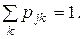 Полученный в результате граф может выглядеть, например, как на Рис. 3.5.

Известно, что существуют преобразования графа, не изменяющие определенные свойства, но упрощающие его структуру. Причем, пользоваться преобразованиями Лапласа функций p_jk(t) более удобно, чем самими функциями p_jk(t). Кроме удобства при написании признаков ветвей графа, функции P_jk(s) позволяют очень просто вычислить временные моменты сигналов. Пусть, например, нас интересуют только те сигналы, которые начинаются с состояния j и кончаются состоянием k. После соответствующих преобразований графа можно получить функцию P_jk(s) в виде степенного ряда P_jk(s) = a₀ + a₁s + a₂s² +...

                                                            с

                                                        2     

                                                    b        d

                     0          a 1       e         3

                                                         f

                                   g

Рис. 3.5. Графическое представление сигнала

Коэффициент а₀ дает безусловную вероятность осуществления перехода j® k, т.е. вероятность появления сигнала любой длительности, начинающегося с j-го символа и заканчивающегося k-м. Величина 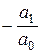 характеризует среднюю длительность такого сигнала; дисперсия длительности определяется величиной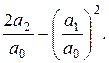

Из полного графа случайного процесса легко определить любую интересующую нас реализацию, выделив в нем соответствующую траекторию. По характеристикам ветвей траектории находится вероятность данной реализации и ее остальные временные статистические характеристики.

Наиболее эффективно граф может быть использован для нахождения статистических характеристик подмножества сигналов, выделяемого по какому-либо признаку.