Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

МАТЕМАТИЧЕСКИЕ МОДЕЛИ СИГНАЛОВ И ПОМЕХ

 

МАТЕМАТИЧЕСКИЕ МОДЕЛИ СИГНАЛОВ И ПОМЕХ

 

Математическое описание сообщений, сигналов и помех

 

В основе математического описания сообщений, сигналов и помех лежат методы теории вероятностей, теории случайных функций и математической статистики. Целью математического описания является разработка математических моделей сообщений, сигналов и помех, необходимых для анализа, синтеза и оптимизации объектов информационной техники. Математические модели позволяют анализировать свойства сообщений, сигналов и помех, а также синтезировать сигналы с требуемыми свойствами.

Понятие «сигнал» имеет неоднозначное толкование. В широком смысле слова под сигналом понимают материальный носитель информации. При этом к сигналам относят как естественные сигналы, так и сигналы, специально создаваемые с определенной целью. Естественными являются, например, световые сигналы, по­зволяющие видеть окружающий мир, космические сигналы. Примером специально создаваемых могут служить сигналы, генерируемые с целью извлечения информации об изменени­ях в объекте или процессе (эталонные сигналы).

В дальнейшем понятие «сигнал», если это не оговорено специально, будет использоваться в узком смысле как сиг­нал, специально создаваемый для передачи сообщения в ин­формационной системе. Материальную основу сигнала со­ставляет какой-либо физический объект или процесс, назы­ваемый носителем (переносчиком) информации (сообще­ния). Носитель становится сигналом в процессе модуля­ции. Параметры носителя, изменяемые во времени в соот­ветствии с передаваемым сообщением, называют информа­тивными.

В качестве носителей информации используются колеба­ния различной природы, чаще всегогармонические, включая частный случай — постоянное состояние (со = 0). В техни­ческих информационных системах наиболее широкое рас­пространение получили носители в виде электрического на­пряжения или тока. Поэтому, рассматривая в дальнейшем модели сигналов, для конкретности,, будем соотносить их с электрическими сигналами.

В носителе u ( t ) = const имеется только один информа­тивный параметр — уровень (например, уровень напряже­ния) . При использовании гармонических электрических ко­лебаний информативными могут статьтакие параметры, как амплитуда, частота, фаза. Колебания принято подразделять на детерминированные и случайные.

Детерминированными называют колебания, которые точно определены в любые моменты времени.

Случайные колебания отличаются тем, что значения их некоторых параметров предсказать невозможно. Они могут рассматриваться как сигналы, когда несут интересующую нас информацию (случайные сигналы), или как помехи, когда мешают наблюдению интересующих нас сигналов.

При изучении общих свойств каналов связи, сигналов и помех мы отвлекаемся от их конкретной физической приро­ды, содержания и назначения, заменяя моделями. Мо­дель — это выбранный способ описания объекта, процесса или явления, отражающий существенные с точки зрения решаемой задачи факторы.

Задачи повышения эффективности функционирования информационных систем связаны с установлением количе­ственных соотношений между основными параметрами, ха­рактеризующими источник информации и канал связи. Поэ­тому при исследовании используют математические модели. Математическое моделирование может быть реализовано различными методами в зависимости от способа, которым определяются интересующие нас показатели.

Фундаментальные исследования базируются на методе аналитического моделирования, заключающемся в созда­нии совокупности математических соотношений, позволяю­щих выявить зависимости между параметрами модели в об­щем виде. При этом широко используются модели, пара­метры которых противоречат физическим свойствам реаль­ных объектов. Например, модель сигнала часто представля­ется суммой бесконечного числа функций, имеющих неогра­ниченную продолжительность (синусоид). Поэтому важно обращать внимание на условия, при которых это не мешает получать результаты, соответствующие наблюдаемым в действительности.

Так как источник сообщений выдает каждое сообщение с некоторой вероятностью, то предсказать точно изменения значения информативного параметра невозможно. Следо­вательно, сигнал принципиально представляет собой слу­чайное колебание и его аналитической моделью может быть только случайный процесс, определяемый вероятностными характеристиками.

Тем не менее в случае детерминированного колебания условно также говорят о детерминированном сигнале. Такой сигнал отображает известное сообщение, которое нет смысла передавать. Ему соответствует модель в виде функции, полностью определенной во времени.

Изучение моделей детерминированных сигналов необхо­димо по многим причинам. Важнейшая из них заключается в том, что результаты анализа детерминированных сигналов являются основой для изучения более сложных случайных сигналов. Это обусловлено тем, что детерминированный сигнал может рассматриваться как элемент множества де­терминированных функций, составляющих в совокупности случайный процесс. Детерминированное колебание, таким образом, представляет собой вырожденную форму случай­ного процесса со значениями параметров, известными в лю­бой момент времени с вероятностью, равной единице. Де­терминированные сигналы имеют и самостоятельное значе­ние. Они специально создаются для целей измерения, на­ладки и регулирования объектов информационной техники, выполняя роль эталонов.

Сущность большинства задач анализа реальных сигналов состоит в том, чтобы эти сигналы представить в виде совокупности простых элементарных сигналов, удобном для последующего анализа их прохождения через те или иные цепи. Например, реальный сигнал может быть представлен в виде суммы ортогональных составляющих (элементарных сигналов)

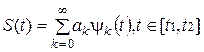
(3.1)

                      

многими способами. Интервал [t₁, t₂] показывает время действия сигнала. Так как система ортогональных функций {y _k(t)}, применяемая для разложения, заранее известна, то сигнал полностью определяется набором весовых коэффициентов a_k, k = 1, 2, ... , для этих функций. При приближенном представлении сигналов, что всегда имеет место в инженерной практике, набор чисел {a_k} конечен. Такие наборы чисел называют спектрами сигналов.

Спектры, как известно из теории связи, являются удобной аналитической формой представления сигналов в рамках линейной теории. Основная задача – правильный выбор системы ортогональных функций (базиса), удобной для последующего анализа прохождения сигнала через те или иные цепи и каналы связи.

Совокупность методов представления сигналов в виде (3.1) называют обобщенной спектральной теорией сигналов.

Представление (3.1) является разложением сигнала по системе базисных функций. К системе базисных функций предъявляют следующие основные требования: для любого сигнала ряд должен сходиться, функции y _k(t) должны иметь простую аналитическую форму; коэффициенты a_k должны вычисляться относительно просто. Этим трем условиям удовлетворяют системы ортогональных функций.

Условие ортогональности нормированной базисной функции имеет вид

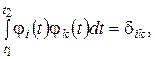
(3.2)

где

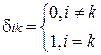
d _ik – символ Кронекера. Систему {φ(t)} называют ортонормированной.

Для детерминированных сигналов наибольшее распространение получили методы спектрального анализа, использующие преобразования Фурье. В этих методах в роли y _k(t) выступают гармонические функции, а роль коэффициентов a_k играют амплитуды гармоник.

Важное значение гармонических сигналов для техники связи обусловлено рядом причин. В частности:

1. Гармонические сигналы инвариантны относительно преобразований, осуществляемых стационарными линейными электрическими цепями. Если такая цепь возбуждена источником гармонических колебаний, то сигнал на выходе цепи остается гармоническим с той же частотой, отличаясь от входного сигнала лишь амплитудой и начальной фазой. 

2. Техника генерирования гармонических сигналов относительно проста.

Кроме гармонического сигнала, для анализа характеристик цепей в технике связи используют еще две очень важные функции: дельта-функцию и функцию единичного скачка.

Дельта-функция δ(t), или функция Дирака, представляющая собой бесконечно узкий импульс с бесконечной амплитудой, расположенный при нулевом значении аргумента функции. «Площадь» импульса тем не менее равна единице:

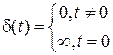
(3.3)

 

 

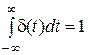
(3.4)

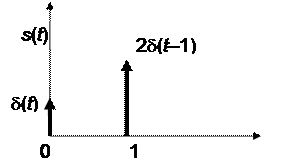Разумеется, сигнал в виде дельта-функции невозможно реализовать физически, однако эта функция очень важна для теоретического анализа сигналов и систем. На графиках дельта-функция обычно изображается жирной стрелкой, высота которой пропорциональна множителю, стоящему перед дельта-функцией (Рис. 3.1).

Рис. 3.1. График сигнала s(t) = δ(t) + 2δ(t – 1)

 

Одно из важных свойств дельта-функции – так называемое фильтрующее свойство. Оно состоит в том, что если дельта-функция присутствует под интегралом в качестве множителя, то результат интегрирования будет равен значению остального подынтегрального выражения в той точке, где сосредоточен дельта-импульс:

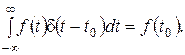
(3.5)

 

Из того факта, что интеграл от дельта-функции дает безразмерную единицу, следует, что размерность самой дельта-функции обратна размерности ее аргумента. Например, дельта-функция времени имеет размерность 1/с, то есть размерность частоты.

Функция единичного скачка σ(t), она же функция Хевисайда, она же функция включения, равна нулю для отрицательных значений аргумента и единице – для положительных. При нулевом значении аргумента функцию считают либо неопределенной, либо равной 1/2:

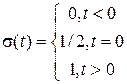
(3.6)

 

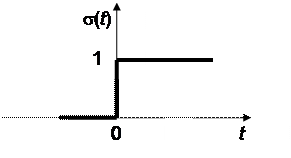График функции единичного скачка приведен на Рис. 3.2.

Рис. 3.2. Функция единичного скачка

 

Функцию единичного скачка удобно использовать при создании математических выражений для сигналов конечной длительности. Простейшим примером является формирование прямоугольного импульса с амплитудой А и длительностью Т: s(t) = A(σ(t) – σ(t – T)).

Вообще, любую кусочно-заданную зависимость можно записать в виде единого математического выражения с помощью функции единичного скачка.

Для случайных сигналов наибольшее распространение получили методы корреляционного и спектрального анализа, основанные на преобразовании Хинчина – Винера. Эти преобразования являются результатом распространения метода Фурье на случайные процессы. При разложении случайных процессов коэффициенты а_к являются случайными величинами, а оптимальные базисы определяются через корреляционные функции этих процессов.

К задачам синтеза сигналов относят задачи определения формы сигналов (структурный синтез) и задачи определения параметров сигналов известной формы (параметрический синтез).