Случайные процессы различаются по степени одно­родности протекания их во времени. В общем случае процесс может иметь определенную тенденцию развития и характеристики, зависящие от начала отсчета времени. Такие случайные процессы называются нестационарными.

Для описания сигнала математическая модель в виде нестационарного случайного процесса подходит наилучшим образом, но неконструктивна в силу своей чрезмерной сложности.

Поэтому очень часто вводят предположение о стационарности случайного процесса, что позволяет сущест­венно упростить математический аппарат исследования. Случайный процесс называют стационарным в узком смысле, если выражения для плотностей вероятности не зависят от начала отсчета времени, т. е. справедливо соотношение

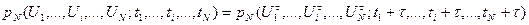   (3.37)

где 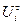— случайная величина, отражающая значение процесса в момент времени  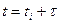(  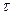— произволь­ное число).

Иначе говоря, стационарность процесса предполагает его существование и статистическую однородность во всем диапазоне времени от 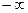 до .

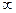Такое предположение противоречит физическим свой­ствам реальных сигналов, в частности тому, что всякий реальный сигнал существует лишь в течение конечного отрезка времени. Однако аналогично установившимся детерминированным процессам случайные процессы, про­текающие в установившемся режиме системы при неиз­менных внешних условиях на определенных отрезках времени, с известным приближением можно рассматри­вать как стационарные.

При решении многих технических задач идут на даль­нейшее упрощение модели, рассматривая случайный про­цесс стационарным в широком смысле. Процесс U ( t ) при­нято называть стационарным в широком смысле, если выполняется условие постоянства математического ожи­дания и дисперсии, а корреляционная функция не зави­сит от начала отсчета времени и является функцией только одного аргумента 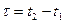,т.е.

,                            (3.38)

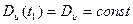,                            (3.39)

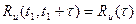.                                     (3.40)

Так как условие постоянства дисперсии является частным случаем требования к корреляционной функции при :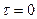

,

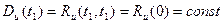то выполнения соотношений (3.38) и (3.40) достаточно, чтобы рассматривать случайный процесс U ( t ) как стацио­нарный.

Всякий стационарный случайный процесс является стационарным в широком смысле. В дальнейшем, если это не оговорено особо, стационарность будем рассмат­ривать в широком смысле.

Случайные процессы, наблюдаемые в устойчиво рабо­тающих реальных системах, имеют конечное время кор­реляции. Поэтому для стационарных процессов, пред­ставляющих практический интерес, справедливо соотно­шение

                                     (3.41)

Если для случайного процесса равенства (3.38), (3.40) не выдерживаются, но на интересующем нас интервале времени изменением указанных параметров можно пренебречь, его называют квазистационарным.

Среди стационарных случайных процессов многие удовлетворяют свойству эргодичности. Оно проявляется в том, что каждая реализация случайного процесса достаточной продолжительности несет практически пол­ную информацию о свойствах всего ансамбля реализа­ций, что позволяет существенно упростить процедуру определения статистических характеристик, заменяя усреднение значений по ансамблю реализаций усредне­нием значений одной реализации за длительный интер­вал времени.

Следовательно, для стационарных эргодических про­цессов справедливы соотношения

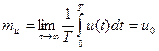                        (3.42)

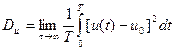                           (3.43)

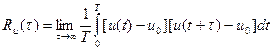              (3.44)

где u ( t ) — конкретная реализация случайного процесса U ( t ).

Результаты исследования случайных процессов в их временном представлении, т.е. с использованием формул (3.42) и (3.44), лежат в основе корреляционной теории сигналов.

Для облегчения практического определения корреляционных функций

в соответствии с (3.44) серийно выпус­каются специальные вычислительные устройства — кор­релометры (корреляторы).

Приведем примеры, с которыми часто имеют дело в теории сигна­лов.