Гауссовский случайный процесс. Удобной моделью помех и некоторых полезных сигналов является стационарный нормальный случайный процесс. Случайные мгновенные значения величины x(t) предполагаются подчиненными нормальному закону (с нулевым средним), т.е. плотность распределения первого порядка выражается формулой

(2.23)

Нормальный (гауссовский) закон распределения случайных величин чаще других встречается в природе. Нормаль­ный процесс особенно характерен для помех в каналах связи. Он очень удобен для анализа. Поэтому случайные процессы, распределение которых не слишком отличается от нормального, часто заменяют гауссовским процессом.

В данном случае рассматривается стационарный и эргодический гауссовский процесс. Поэтому под т_х и σ_х можно подразумевать соответственно постоянную составляющую и среднюю мощность флуктуационной составляющей одной (до­статочно длительной) реализации случайного процесса.

Графики плотности вероятности при нормальном законе для некоторых значений σ_х изображены на Рис. 3.4. Функ­ция р(х) симметрична относительно среднего значения. Чем больше σ_х, тем меньше максимум, а кривая становится более по­логой (площадь под кривой р(х) равна единице при любых значениях σ_х).

                                           p

                                                           σ_х=0,5  

                                                   σ_х=1

                                                             σ_х=2

Рис. 3.4. Одномерная плотность вероятности нормального распределения

Широкое распространение нормального закона распреде­ления в природе объясняется тем, что при суммировании до­статочно большого числа независимых или слабо зависи­мых случайных величин распределение суммы близко к нор­мальному при любом распределении отдельных слагаемых.

Это положение, сформулированное в 1901 г. А.М. Ляпуно­вым, получило название центральной предельной теоремы.

Наглядными физическими примерами случайного процес­са с нормальным законом распределения являются шумы, обусловленные тепловым движением свободных электронов в проводниках электрической цепи или дробовым эффектом в электронных приборах. Не только шумы и помехи, но и по­лезные сигналы, являющиеся суммой большого числа незави­симых случайных элементарных сигналов, например, гармонических колебаний со случайной фазой или амплитудой, часто можно трактовать как гауссовские случайные процессы.

На основе функции р(х) можно найти относительное время пребывания сигнала x(t) в определенном интервале уров­ней, отношение максимальных значений к среднеквадратическому (пик-фактор) и ряд других важных для практики параметров случайного сигнала.

Отношение времени пребывания x(t) в заданном интер­вале к общему времени наблюдения можно трактовать как вероятность попадания x(t) в указанный интервал. При этом следует заметить, что данные о распределении вероятностей не дают никаких представлений о поведении функции x(t) во времени.

 Белый шум используют как модель наиболее тяжелого вида помехи в каналах связи. Он является стационарным случайным процессом с постоянной спектральной плотностью W_x(w) = W₀ = const. Если в выражение для корреляционной функции

Rx(t) =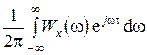

(3.46)

подставить W₀, то получим

где δ(τ) – дельта-функция.

Для белого шума с бесконечным и равномерным спект­ром корреляционная функция равна нулю для всех значений τ, кроме τ = 0, при котором R_x(0) обращается в бесконеч­ность. Подобный шум, имеющий игольчатую структуру с бес­конечно тонкими случайными выбросами, иногда называют дельта-коррелированным процессом. Дисперсия белого шума бесконечно велика. Если спектр W_x(ω) ограничен сверху частотой ω_В, то такой процесс называется квазибе­лым шумом.

Сигнал как колебание со случайными огибающей и фазой. Понятия амплитуды и фазы, введенные первоначально для гармонических сигналов, с помощью модуляции были обобщены на сигналы, которые уже не являются гармоническими. Можно обобщить их на произвольные сигналы: пока чисто фор­мально можно задать такие функции A(t) и y(t), чтобы для заданной функции s(t) было выполнено равенство

A(t) и y(t) можно интерпретировать как «огибающую» и «фазу» колебания с частотой ω₀. Оказывает­ся, свобода выбора в задании функций A и y при определенных условиях весьма ограничена. Комплекс этих условий получил название узкополосности сигнала x(t).

Очень наглядным является векторный ва­риант модели (3.48): A и y можно рассматри­вать как полярные координаты некоторого вектора. Тогда всякое гармоническое колебание s(t) = S ×cos(ω₀t + φ), имеющее частоту ω₀, изобразится как постоянный вектор с ам­плитудой S и углом φ к направлению, принятому за ось Ох.