Рассмотрим, какие функции целесообразно выбирать в качестве базисных при анализе инвариантных во времени линейных систем. При исследовании таких сис­тем решения всегда содержат комплексные экспоненциальные функции времени. Детерминированные сигна­лы, описываемые экспоненциальными функциями време­ни, при прохождении через инвариантные во времени линейные системы не изменяются по своему характеру, что является следствием инвариантности класса экспо­ненциальных функций относительно операций дифферен­цирования и интегрирования.

Широко используются представления детерминиро­ванных сигналов с применением базисных функций е^pt как при р = ±jω (преобразование Фурье), так и при p = s+jω (обобщенное преобразование Фурье, извест­ное как преобразование Лапласа).

До сих пор мы не касались физической интерпретации базисных функций. Для чисто математических преобра­зований она не обязательна. Однако такая интерпрета­ция имеет безусловные преимущества, так как позволяет глубже вникнуть в физический смысл явлений, протекаю­щих в системах при прохождении сигналов.

Использование экспоненциальных базисных функций в преобразовании Фурье комплексно-сопряженными пара­ми (с положительным и отрицательным параметром ω) позволяет в соответствии с формулой Эйлера 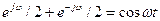 представить сложный детерминированный сигнал в виде суммы гармонических составляющих. Поскольку пара­метр ω в этом случае имеет смысл круговой частоты, результат такого преобразования называют частотной формой представления сигнала.

В силу указанных преимуществ разложение сигналов по системе гармонических базисных функций подверг­лось всестороннему исследованию, на основе которого была создана широко известная классическая спектраль­ная теория сигналов.

В частотном виде могут представляться как периодические, так и непериодические детерминированные сигналы.

Строго говоря, в реальных условиях периодические сигналы не существуют, так как идеальный периодический сигнал бесконечен во времени, а всякий реальный сигнал имеет начало и конец. Однако во многих случаях конечностью времени действия сигнала можно пренебречь и для анализа допустимо использовать аппарат, пригодный для идеальных периодических сигналов.

Спектры периодических сигналов. Простейшим периодическим сигналом является гармони­ческое колебание (тока, напряжения, заряда, напряженности поля), определяемое законом

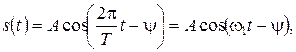
(3.7)

при -¥ < t < +¥. Здесь А, Т, ω_l, ψ – постоянные амплитуда, период, час­тота и фаза.

Указание этих параметров, образующих спектр гармонической функции, и будет ее частотным представлением.

Обычно прибегают к графическому изображению спектра. По оси абсцисс наносятся частоты, по оси ординат – амплитуды и фазы. Для удобства вычерчиваются два графика, представляющих амплитудный и фазовый спектры соответственно. Очевидно, для гармонического сигнала каждый из этих спектров изобразится единственной точкой. График становится более наглядным, если из указанной точки опустить на ось частот перпендикуляр, который будет изображать так называемую спектральную линию.

Гармонический сигнал находит широкое применение на практике, в частности, при регулировке устройств обработки информации и снятии их амплитудных и частотных характеристик.

Произвольный детерминированный сигнал опреде­ляется как некоторая заданная функция времени x(t). В настоящее время в большинстве слу­чаев произвольный детерминированный сигнал пред­ставляется в виде надлежащим образом выбранной сово­купности элементарных сигналов. Основой для такого рассмотрения являются ряды Фурье.

Итак, любой сложный периодический сигнал может быть представлен в виде суммы элементарных гармоничес­ких сигналов, действующих при -¥ < t < +¥.

Пусть заданная на интервале t₁ £ t £ t₂ функция s(t) перио­дически повторяется с частотой , где Т – период по­вторения, причем выполняются следующие условия (условия Дирихле):

1) в любом конечном интервале функция s(t) должна быть непрерывна или должна иметь конечное число разрывов пер­вого рода;

2) в пределах одного периода функция s(t) должна иметь конечное число экстремальных значений.

Известны две формы разложения в ряд Фурье: тригонометрическая и комплексная. Тригонометрическая форма разложения выражается в виде

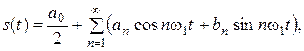
(3.8)

    n = 1, 2, ... (3.10)

 или, что равносильно,

(3.9)

здесь  – постоянная составляющая (действующее зна­чение); а_n и b_n – амплитуды косинусоидальных и синусоидаль­ных членов разложения s(t).

Эти величины определяются выражениями:

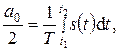
	(3.7)
	(3.8)
	(3.9)

Амплитуда (модуль) и фаза (аргумент) n-й гармоники вы­ражаются через а_n и b_n следующим образом:

	(3.10)
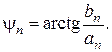
	(3.11)

Ряд Фурье в комплексной форме обычно записывается следующим образом:

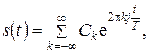
	(3.12)
	(3.13)

Таким образом, если функция x(t) имеет конечную длительность (т.e. ограничена по времени) и удовлетво­ряет указанным выше условиям, она может быть сколь угодно точно представлена суммой элементарных детер­минированных сигналов типа синусоиды. При этом каждый элементарный сигнал характеризуется своей амплитудой, определяемой формулой (3.10), и частотой 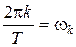. Графически это можно изобразить так, как показано на

Рис. 3.3. Расстояние между соседними ча­стотами гармоник по оси частот равно .

Рис. 3.3. Коэффициенты ряда Фурье

Следует отметить, что приведенным выше условиям Ди­рихле удовлетворяют все физически осуществимые сигналы. Поэтому при представлении периодических сигналов в виде рядов Фурье эти условия в практике не приходится специ­ально оговаривать.

В тех случаях, когда сигнал представляет собой функ­цию, четную относительно t, т.е. s(t) = s(–t), в тригонометричес­кой записи остаются только косинусоидальные члены, так как коэффициенты b_n в соответствии с (3.9) обращаются в нуль. Для нечетной относительно t функции s(t), наоборот, в нуль обращаются коэффициенты а_п (3.8), и ряд со­стоит только из синусоидальных членов.

Таким образом, структура частотного спектра периодического сигнала полностью определяется двумя характеристиками – ампли­тудной и фазовой, т.е. модулем и аргументом кoмплeкcнoй амплитуды [(3.10) и (3.11)]. Наглядное представление о «ширине» спектра и относительной величине отдельных eго составляющих дает графическое изображение спектра (см.

Рис. 3.3). Здесь по оси ординат отложены модули амплитуд, по оси абсцисс – частоты гармоник.

Спектр периодической функции состоит из отдельных «линий», соответствующих дискретным частотам: 0, ω₁, 2ω₁, ..., nω₁. Отсюда и название – линейчатый, или дискретный, спектр.

Существует очень важное понятие – практическая ширина спектра сигнала. Интуитивно ясно, что если полоса пропускания какого-либо устройства недостаточно широкая, чтобы пропустить все гармоники, существенно влияющие на форму сигнала, то сигнал на выходе этого устройства исказится. Таким образом, можно сказать, что ширина полосы пропускания устройства не должна быть уже ширины спектра сигнала.

Существует несколько критериев для определения практической ширины спектра сигнала. Например, ширину спектра можно определять как область частот, в пределах которой сосредоточена основная энергия сигнала (например, 95 %). Можно отбрасывать все гармоники с амплитудами, меньшими 1 % максимальной амплитуды в спектре, тогда частоты оставшихся гармоник и определят ширину спектра сигнала.

Однако независимо от критерия, по которому определяют ширину спектра сигнала, можно выделить такие общие для всех сигналов закономерности: чем круче фронт сигнала, чем короче импульсы и чем больше пауза между импульсами, тем шире во всех этих случаях спектр сигнала, т.е. тем медленнее убывают амплитуды гармоник с ростом их номера.

 Хотя условия одновременного ограничения длительности и полосы частот не могут быть выполнены в точности, однако можно ограничить спектр полосой F и иметь малые значения сигнала вне интервала Т.

Значение рядов Фурье в современной технике очень ве­лико. Основанный на формулах (3.8 и (3. гармонический ана­лиз сложных периодических сигналов в сочетании с принци­пом наложения (суперпозиции) представляет собой эффек­тивное средство для изучения влияния линейных систем на прохождение сигналов.

Если на входе линейной системы, характеристики кото­рой известны, существует сигнал e(t) (электродвижущая сила), то для нахождения выходного сигнала достаточно учесть ам­плитудные и фазовые изменения, претерпеваемые каждой из гармонических составляющих сигнала при прохождении че­рез рассматриваемую систему. Условие линейности системы позволяет рассматривать прохождение каждой из гармоник сигнала независимо от всех остальных гармоник.

Спектры непериодических сигналов. В реальных системах передачи всегда действуют непе­риодические сигналы, так как все сигналы имеют конечную длительность.

Непериодический сигнал можно рассматривать как периодический с периодом T ® ¥. При этом разность частот между соседними гармониками стремится к нулю. Спектр становится сплошным, амплитуды – бесконечно малыми. При Т ® ¥ частота ω₁ превращается в dω, пω₁ – в те­кущую частоту ω, а операция суммирования — в операцию интегрирования.

Если функция x(t) не ограничена во вре­мени, удовлетворяет условиям Дирихле на любом конечном интервале и до­полнительно удовлетворяет условию

(3.14)

т.е. интеграл (3.19) сходится, то ее можно представить следующим интегральным выражением:

(3.15)

называемым интегралом Фурье.

Внутренний интеграл, являющийся функцией ω, обозна­чим

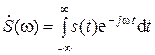
(3.16)

После подстановки (3.16) в выражение (3.15) получаем

(3.17)

Выражения (3.16) и (3.17) представляют собой прямое и обратное преобразования Фурье. S(w) называется спектральной плотностью или спектральной характеристикой функции s(t). Выражение (3.17) представляет собой непериодическую функ­цию в виде суммы (интеграла) гармонических колебаний с бес­конечно малыми амплитудами.

Из анализа преобразований Фурье вытекает следующее важное поло­жение: огибающая сплошного спектра (модуль спектральной плотности) непериодической функции и огибающая линейчатого спектра периодической функции (получен­ной из непериодической путем продолжения ее с перио­дом Т) совпадают по форме и отличаются только мас­штабом.

Поскольку спектральная характеристика – комплексная величина, то ее можно представить в виде

,

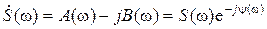(3.18)

где А(ω) и В(ω) – соответственно действительная и мнимая части спектральной плотности; S(ω) и ψ(ω) – амплитудно-частотная (АЧХ) и фазо-частотная (ФЧХ) характеристики спектральной плотности.

Непосредственно из формулы (3.16) вытекают следующие выражения для А(ω) и В(ω):

	(3.19)
	(3.20)

Очевидно также, что модуль и фаза спектральной плотности определяются выражениями:

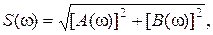
	(3.21)
	(3.22)

Как и в случае ряда Фурье, модуль спектральной плотности есть функция четная, а фаза – нечетная относительно частоты ω.

Итак, структура спектра непериодического сигнала полностью определяется функциями частоты S(w) (спектром амплитуд) и j(w) (спектром фаз).