Мущанов В.Ф., Жук Н.Р.
КОНСПЕКТ ЛЕКЦИЙ по дисциплине
«СТРОИТЕЛЬНАЯ МЕХАНИКА»
(для студентов строительных специальностей)
Часть 3
| Утверждено на заседании |
| кафедры теоретической и |
| прикладной механики |
| Протокол № 1 от 29.01.2010 |
| Заведующий кафедры |
| проф. Мущанов В.Ф. |
Макеевка, 2010
Конспект лекций. Строительная механика. Часть 3. В.Ф. Мущанов, Н.Р. Жук. – 69 с.
Конспект лекций предназначен для студентов строительных специальностей вузов. Включает в себя три раздела специального курса строительной механики. Метод конечных элементов, применительно к расчету плоских стержневых систем, устойчивость сооружений и основы динамики сооружений. Теоретический материал иллюстрируется рисунками, приводятся примеры решения задач.
Рецензент доц. Демидов А.И.
содержание
Лекция 1. Приближенные методы расчета в строительной механике....... 4
Лекция 2. Метод конечных элементов в расчетах плоских стержневых систем............................................................................................................................. 6
Лекция 3. Матрица преобразований (направляющих косинусов)........... 11
Лекция 4. Порядок расчета стержневых систем методом конечных элементов........................................................................................................................... 13
Приложение. Формирование матрицы жесткости плоского треугольного конечного элемента в локальной системе осей координат........................ 19
Лекция 5. Устойчивость сооружений........................................................... 21
Лекция 6. Статический метод исследования устойчивости стержневых систем........................................................................................................................... 24
Лекция 7. Расчет статически неопределимых рам на устойчивость методом перемещений.................................................................................................... 29
Лекция 8. Понятие о расчете на устойчивость круговых арок постоянного сечения.............................................................................................................. 35
Лекция 9. Устойчивость составных стержней (сквозных колонн)........... 41
Лекция 10. Расчет на устойчивость колонны ступенчатого сечения....... 45
Лекция 11. Потеря устойчивости плоской фермы изгиба тонкой полосы и двутавровой балки.......................................................................................... 47
Лекция 12. Основы динамики сооружений................................................. 51
Лекция 13. Колебания систем с одной степенью свободы......................... 53
Лекция 14. Свободные колебания систем без учета их сил сопротивления 55
Лекция 15. Вынужденные колебания систем с одной степенью свободы при действии вибрационной нагрузки................................................................ 56
Лекция 16. Свободные колебания систем с двумя степенями свободы... 60
Лекция 17. Колебания систем с бесконечным числом степеней свободы 62
Лекция 18. Метод замены распределенных масс сосредоточенными...... 67
Приложение. Формирование матрицы жесткости плоского треугольного конечного элемента в локальной системе осей координат
Для расчета конструкций, испытывающих плоское напряженное состояние, плоский треугольный конечный элемент является одним из наиболее удобных типов конечных элементов, т.к. позволяет наиболее просто и удобно получить на конструкции сетку узлов требуемой густоты.
Рассмотрим процесс формирования матрицы жесткости плоского треугольного 3-х узлового конечного элемента с узлами i, j, m, обозначенными в направлении обхода против часовой стрелки.
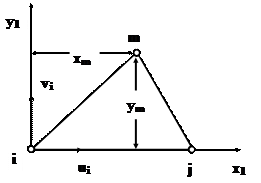 |
К построению матрицы жесткости треугольного КЭ
Смещения в узле имют 2 компонента - ui и vi. Тогда вектор узловых смещений элемента может быть представлен как
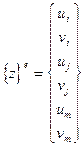 (1)
(1)
Самое простое представление смещения u и v точек с координатами x и y внутри элемента через смещения узловых точек может быть получено на основе использования 2-х линейных многочленов:
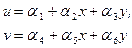 (2)
(2)
Постоянные a1 - a6 можно получить, решая две системы из 3-х уравнений, введя координаты узлов и приравняв их смещения соответствующим узловым смещениям:
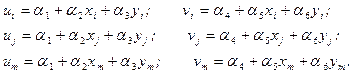 (3)
(3)
Подставив решения систем (3) в выражения (2) окончательно получим выражения для u и v
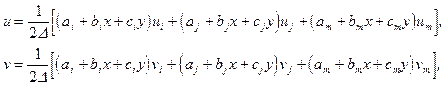 (4)
(4)
где D - площадь треугольника,
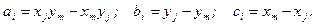
Коэффициенты aj, bj, cj, am, bm, cm можно получить циклической перестановкой индексов в последовательности i, j, m.
Относительная деформация в любой точке элемента определяется с помощью трех компонентов, вносящих вклад во внутреннюю работу, которая с помощью уравнений (4) может быть записана как
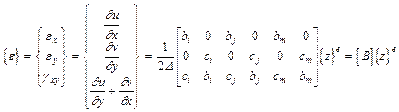 (5)
(5)
Учитывая, что для треугольного элемента постоянной толщины общее выражение для матрицы жесткости может быть упрощено, т.е.
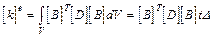 (6)
(6)
и учитывая, что матрица упругости ( закона Гука) для случая плоского напряженного состояния имеет вид
 (7)
(7)
окончательно выражение для матрицы жесткости плоского треугольного элемента имеет вид:
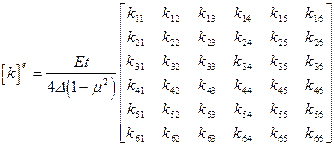 (8)
(8)
где 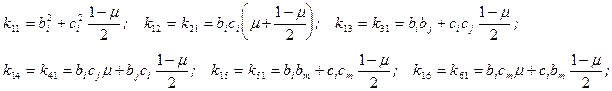
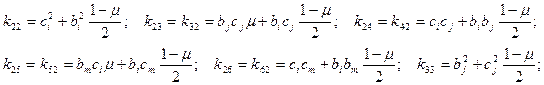

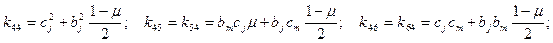
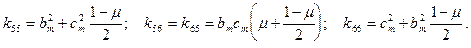
Использование полученной матрицы жесткости в дальнейших конечно-элементных операциях ничем не отличается от использования матрицы жесткости стержневого конечного элемента. Естественно, результатом расчета в этом случае будут усилия соответствующие компонентам перемещений, указанным на Рис. , т.е.  , которые могут быть преобразованы к напряжениям в центре тяжести конечного элемента
, которые могут быть преобразованы к напряжениям в центре тяжести конечного элемента  .
.
Степени свободы систем
Системы в динамике сооружений разделяются по числу степеней свободы.
Степенью свободы системы называется число независимых геометрических параметров, определяющих положение всех масс конструкции в любой момент времени.
Положение любой массы на плоскости характеризуется тремя геометрическими параметрами или степенями свободы.

У
j
у
0 х Х
Если эту массу условно представить в виде точки, то ее положение на плсокости характеризуется двумя параметрами, а в пространстве - тремя.
У
 m
m
y
Х
x
Всякая распределенная масса на упругой деформируемой системе, представляемая как бесконечно большое количество бесконечно малых масс, будет иметь бесконечное число степеней свободы.
Для определения степени свободы системы необходимо каждую массу системы закрепить связями от всех возможных перемещений. Количество вводимых стержней и определяет степень свободы системы.
m1
Масса рамы мала по сравнению
с сосредоточенными массами,
поэтому ней пренебрегают.
 m2
m2
Ст. свободы = 6
Если пренебречь поворотами масс и считать их точечными.
В практических расчетах часто пренебрегают
m1 перемещениями масс за счет растяжения или
 сжатия стержней, тогда
сжатия стержней, тогда
m2 m1

m2
ст. свободы =4
m1
 ст. свободы =3
ст. свободы =3
ст. свободы =1
Методы динамики сооружений
В динамике сооружений используют два основных метода исследований:
1. Кинематический метод, суть которого заключается в том, что конструкция в каждый момент времени рассматривается в равновесии под действием заданных динамических нагрузок и сил инерции всех ее масс.
2. Энергетический метод основан на исследовании полной потенциальной энергии системы с учетом инерционных сил.
Мущанов Владимир ФилиПпович
Жук Николай Романович
Мущанов В.Ф., Жук Н.Р.
КОНСПЕКТ ЛЕКЦИЙ по дисциплине
«СТРОИТЕЛЬНАЯ МЕХАНИКА»
(для студентов строительных специальностей)
Часть 3
| Утверждено на заседании |
| кафедры теоретической и |
| прикладной механики |
| Протокол № 1 от 29.01.2010 |
| Заведующий кафедры |
| проф. Мущанов В.Ф. |
Макеевка, 2010
Конспект лекций. Строительная механика. Часть 3. В.Ф. Мущанов, Н.Р. Жук. – 69 с.
Конспект лекций предназначен для студентов строительных специальностей вузов. Включает в себя три раздела специального курса строительной механики. Метод конечных элементов, применительно к расчету плоских стержневых систем, устойчивость сооружений и основы динамики сооружений. Теоретический материал иллюстрируется рисунками, приводятся примеры решения задач.
Рецензент доц. Демидов А.И.
содержание
Лекция 1. Приближенные методы расчета в строительной механике....... 4
Лекция 2. Метод конечных элементов в расчетах плоских стержневых систем............................................................................................................................. 6
Лекция 3. Матрица преобразований (направляющих косинусов)........... 11
Лекция 4. Порядок расчета стержневых систем методом конечных элементов........................................................................................................................... 13
Приложение. Формирование матрицы жесткости плоского треугольного конечного элемента в локальной системе осей координат........................ 19
Лекция 5. Устойчивость сооружений........................................................... 21
Лекция 6. Статический метод исследования устойчивости стержневых систем........................................................................................................................... 24
Лекция 7. Расчет статически неопределимых рам на устойчивость методом перемещений.................................................................................................... 29
Лекция 8. Понятие о расчете на устойчивость круговых арок постоянного сечения.............................................................................................................. 35
Лекция 9. Устойчивость составных стержней (сквозных колонн)........... 41
Лекция 10. Расчет на устойчивость колонны ступенчатого сечения....... 45
Лекция 11. Потеря устойчивости плоской фермы изгиба тонкой полосы и двутавровой балки.......................................................................................... 47
Лекция 12. Основы динамики сооружений................................................. 51
Лекция 13. Колебания систем с одной степенью свободы......................... 53
Лекция 14. Свободные колебания систем без учета их сил сопротивления 55
Лекция 15. Вынужденные колебания систем с одной степенью свободы при действии вибрационной нагрузки................................................................ 56
Лекция 16. Свободные колебания систем с двумя степенями свободы... 60
Лекция 17. Колебания систем с бесконечным числом степеней свободы 62
Лекция 18. Метод замены распределенных масс сосредоточенными...... 67
Лекция 1. Приближенные методы расчета в строительной механике
Большинство задач строительной механики, связанных с исследованием напряженно-деформированного состояния конструкций и их элементов (стержней, пластин, оболочек) сводится, как правило, к решению одного или нескольких дифференциальных уравнений равновесия элемента, соответственно с одним или несколькими неизвестными.
Точное решение таких уравнений (решение в замкнутом виде) не представляет затруднений лишь в некоторых элементарных случаях. При решении реальных задач часто приходится сталкиваться с таким объемом вычислительных работ, что от точного решения отказываются, а во многих случаях точное решение задачи вообще невозможно, т.к. граничные условия или условия на контуре просто не выражаются в аналитической форме. Поэтому, как правило, при решении практических задач приходится прибегать к приближенным методам решения.
Приближенные методы решения задач могут быть разбиты на две основные группы:
1. Вариационные методы, которые дают приближенные аналитические выражения искомой функции (функции перемещений или функции внутренних усилий).
2. Численные методы, которые дают значения искомой функции при тех или иных значениях аргумента.
К первой группе относятся вариационные методы Ритца, Бубнова-Галеркина, метод Треффца и другие.
Ко второй группе относятся метод сеток и его более совершенная модификация - метод конечных элементов, а также ряд графических и полуграфических методов таких, как, например, метод прямых, метод коллокаций и другие.
Преимущество вариационных методов заключается в том, что задача сводится обычно к решению системы двух, трех, редко четырех уравнений, которые дают хорошее приближение к действительному состоянию сооружения. К их недостаткам следует отнести то, что возможности вариационных методов ограничены сложными контурами и сложными законами распределения внешней нагрузки, т.к. применение вариационных методов требует, чтобы было, хотя бы в приближенной форме, определено аналитическое выражение внешней нагрузки, деформированной упругой поверхности элемента и др. условий задачи.
Численные методы, в сравнении с вариационными, имеют более универсальный характер, т.к. не требуют аналитических выражений условий задачи. Однако численные методы обладают рядом недостатков. Так, для получения удовлетворительного решения они требуют нанесения на исследуемую область густой сетки или разбиения на достаточно большое число элементов, что неизбежно влечет за собой решение систем алгебраических уравнений с большим числом неизвестных, что становится возможным только при наличии ЭВМ. Кроме того, численные методы часто приводят к неточности решений, особенно в местах приложения сосредоточенных сил, при наличии острых углов, подкреплений и т.д., т.е. там, где нарушается гладкость полей переменных.
Весьма существенным недостатком численных методов является то, что они не дают аналитического выражения искомой функции, а, следовательно, для определения параметров напряженно-деформированного состояния в данной области приходится вычислять эти величины во всех узлах стыковки элементов, т.е. получать массу ненужной информации для тех областей, которые нас совершенно не интересуют.
Таким образом, выбор метода расчета при рассмотрении конкретной упругой системы зависит от постановки задачи и исходных условий, а также от вооруженности расчетчика вычислительной техникой.
Дата: 2019-02-19, просмотров: 352.