Дана схема электрическая из 9 элементов:
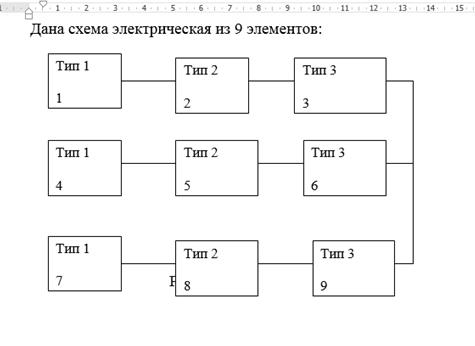
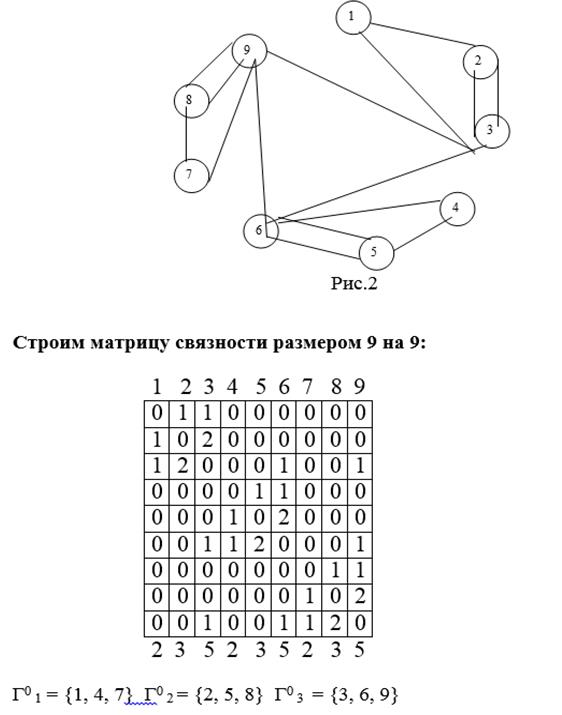

Рис.1
По схеме строим граф, в котором вершины моделируют элементы, а рёбра – электрические цепи:

Рис.2
Строим матрицу связности размером 9 на 9:
1 2 3 4 5 6 7 8 9
| 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 2 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 2 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 0 | 2 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 2 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 2 |
| 0 | 0 | 1 | 0 | 0 | 1 | 1 | 2 | 0 |
2 3 5 2 3 5 2 3 5
Г01 = {1, 4, 7} Г0 2 = {2, 5, 8} Г0 3 = {3, 6, 9}
R12= 2 5 8
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
R13 = 3 6 9
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
R23 = 3 6 9
| 2 | 0 | 0 |
| 0 | 2 | 0 |
| 0 | 0 | 2 |
Г11 = {1 - 2, 4 - 5, 7 - 8} М1 1 = {3, 6, 9}
Г12 = {1 - 3, 4 - 6, 7 - 9} М1 2 = {2, 5, 8}
Г13 = {2 - 3, 5 - 6, 8 - 9} М1 3 = {1, 4, 7}
1 2 4 5 7 8
| 3 6 9 | 1 2 | 0 0 | 0 0 |
| 0 0 | 1 2 | 0 0 | |
| 0 0 | 0 0 | 1 2 |
R1 11 =
1 3 4 6 7 9
| 2 5 8 | 1 2 | 0 0 | 0 0 |
| 0 0 | 1 2 | 0 0 | |
| 0 0 | 0 0 | 1 2 |
R1 22 =
2 3 5 6 8 9
| 1 4 7 | 1 2 | 0 0 | 0 0 |
| 0 0 | 1 2 | 0 0 | |
| 0 0 | 0 0 | 1 2 |
R1 33 =

Рис. 3

Рис. 4
Для автоматизированного решения задачи компоновки применяется ряд алгоритмов.
1. Последовательный алгоритм, использующий матрицу смежности. Идея последовательного алгоритма состоит в поочередной компоновке частей графа от первой до последней.
2. Последовательный алгоритм, использующий матрицу цепей. Принципиальные электрические схемы соединения многоконтактных элементов (например, микросхем и микросборок) удобно представлять гиперграфом Q и записывать в виде матрицы цепей (Аналогичен методу максимальной конъюнкции - минимальной дизъюнкции).
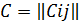 mxk
mxk
где m — число элементов схемы; k — число выводов многоконтактных элементов.
Элемент матрицы Сij означает номер электрической цепи, которая подключается к j-му выводу i-го много-контактного элемента. Если контакт свободен, то cij = 0. Оптимальному разбиению схемы на n частей Qi, Q2. •••, Qn соответствует такое разбиение матрицы С на подматрицы С1, С2..... Сn, при котором число связей между частями минимально. Критерий оптимальности в этом случае записывается в виде
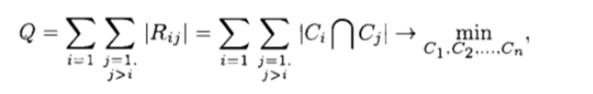
где Rij — число связей между i-й и j-й частями.
Рассмотренный алгоритм компоновки применительно к схемам с многоконтактными элементами позволяет с помощью простых операций оптимальным образом разбить исходную схему на требуемое количество частей
3. Итерационный алгоритм, использующий матрицу смежности.
Идея итерационного алгоритма заключается в перестановках вершин или групп вершин из одной части графа в другую, до тех пор, пока после многократного применения одних и тех же операций не будет получено минимальное число связей между частями.
В общем случае алгоритм состоит из двух этапов:
1) начальное «разрезание» графа (например, механическое деление матрицы смежности на части) — это вспомогательный этап;
2) основной этап, в ходе которого выполняется итерационное улучшение решения на основе парного или группового обмена вершин из различных частей.
Несмотря на то, что итерационный алгоритм позволяет достичь оптимального результата, его недостатком является наличие большого числа громоздких процедур, связанных с перестановкой элементов.
4. Последовательно-итерационный алгоритм.
Данный алгоритм решения задачи компоновки отличается от итерационного тем, что первоначально группы (части) графа G(V, R) формируются не произволь-но, а на основе простых операций последовательного алгоритма. Это позволяет значительно сократить число трудоемких в вычислительном отношении итераций обмена вершинами между частями. Таким образом, в этом комбинированном алгоритме объединены достоинства последовательного и итерационного алгоримов.
Последовательно-итерационный алгоритм позволяет сократить число итераций и обеспечивает оптимальное решение.
5. Генетический алгоритм
В последние годы широкое применение для решения конструкторских задач находят генетические алгоритмы (ГА).
В общем случае в этих алгоритмах задаются структура хромосомы, способы рекомбинации и условия завершения эволюции.
Хромосома играет роль вектора управляемых параметров, она состоит из генов и содержит информацию об их значениях. Выделяют хромосомы родителей и потомков. На начальном этапе решения задачи формируются хромосомы родителейи рассчитывается показатель (критерий), характеризующий предпочтительность каждой хромосомы (особи). Затем отбираются «лучшие» родительские хромосомы для получения хромосом потомков. Операция рекомбинации (скрещивания, кроссовера) обычно выполняется по схеме (2;2), т. е. два родителя — два потомка. Точка разрезания пары хромосом родителей может выбираться случайным образом. На последующих этапах оцениваются предпочтительности хромосом потомков и из них выбираются пары для рекомбинации. В качестве условий окончания эволюционного процесса селекции может использоваться достижение некоторого значения критерия либо выполнение заранее задаваемого числа рекомбинаций.


Дата: 2019-02-19, просмотров: 410.