Под задачей компоновки КС понимаются задачи объединения модулей низшего (i — 1)-го уровня в модули более высокого i-го уровня по заданному критерию или набору критериев оптимиза­ции и при наличии заданных ограничений.

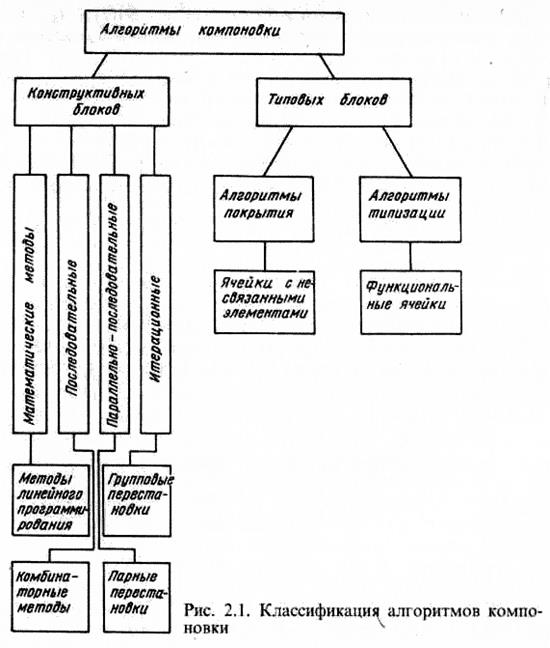
Среди методов компоновки КС РЭС выделяют два характерных класса. К первому классу относятся такие, в которых осуществляется разбиение КС на части (блоки) с учетом таких ограничений, как число элементов в блоках, число внешних выводов на блоках, суммарная площадь, занимаемая элементами и соединениями, и т. д. Основными критериями для такого разбиения являются следующие:

число образующихся блоков;

число межузловых соединений или внешних выводов на блоках;

задержки в распространении сигналов;

электро-магнито - тепловая совместимость элементов и т. д.

Задачи такого вида возникают при разбиении КС на блоки большей степени сложности, к которым не предъявлены требова­ния в отношении схемной унификации. Это задачи распределения ТЭЗ по панелям, микросборок по печатным платам, разбиение КС на БИС, СБИС. К первому классу задач компоновки относят такие, в которых критерии оптимизации и ограничения могут быть сведены к определенным конструктивным параметрам расположения отдельных элементов и их межсоединений. Эти задачи называются задачами компоновки конструктивных частей (блоков).

Второй класс образуют такие методы, в которых кроме конструктивных характеристик образующихся частей существенны и их функциональные характеристики. Они возникают на этапе перехода от функциональных (логических) схем ЭВА к КС, ориентированным на заданную систему элементов, состоят в на­значении элементов логической схемы в типовые модули из заданного набора. Указанный класс называют методом покрытия или задачами компоновки типовых блоков. Основными критери­ями при покрытии схем являются следующие:

число модулей, необходимых для покрытия исходной схемы;

число межмодульных соединений;

число типов используемых модулей;

число неиспользованных элементов во всех модулях схемы и т. д.

В качестве ограничений выступают конструктивные и функцио­нальные характеристики типовых модулей, такие как:

максимально допустимое число элементов (i—1)-го уровня в модулях 

i-го уровня;

максимально допустимое число выводов модуля i-го уровня;

ограничения на совместную работу модулей (i— 1)-го уровня и т. д.

Задачи компоновки являются классическими примерами много­критериальной оптимизации (ЗМО).

Для алгоритмизации и формального решения задачи произво­дится переход от КС к графу, к мультиграфу, к гиперграфу.

Задача типизации

Рассмотрим задачу типизации. Типизация, как отмечалось,— это разбиение схемы на части с минимизацией номенклатуры частей разбиения. В зависимости от постановки задачи проектиро­вания различается постановка задачи типизации. Так, при проекти­ровании твердотельных БИС под однотипными понимают ТЭК, имеющие одинаковый состав элементов. При этом не оговаривает­ся, различаются ли в ТЭК схемы соединений. При решении задачи компоновки часто добавляется требование совпадения схем соединений ТЭК с точностью до элемента.

Однотипными называются ТЭК, имеющие одинаковый состав элементов и одинаковую КС с точностью до инвариантного контакта (ТЭК функционально одинаковы). В этом случае задача типизации формулируется А. М. Бершадским как задача выделе­ния в графе изоморфных подграфов. Поскольку элементы КС могут быть различных типов, то в общем случае используются графы G* (с весами на вершинах и ребрах).

Задача выделения в графе G* изоморфных подграфов форму­лируется следующим образом: найти разбиение графа G* на множество групп Г = {Г1, Г2, ..., Гf} изоморфных подграфов Г_i, удовлетворяющих следующим условиям:

любые два подграфа G_ij и G_i,m, принадлежащие произволь­ной группе разбиения Г_i должны быть изоморфны;

множества вершин любых двух подграфов разбиения не должны пересекаться;

число вершин любого подграфа разбиения не должно превышать заданное (конструктивное ограничение, связанное с числом элементов на типовом элементе конструкции);

4) суммарное число внешних ребер каждого подграфа не должно превышать заданное (конструктивное ограничение, связанное с числом элементов разъема или длиной параметра корпуса ТЭК).

Критерием оптимальности при типизации является минималь­ное число групп изоморфных подграфов, полученных в результате разбиения, т. е. minf_φ Для решения задачи типизации путем сведения ее к задаче выделения в графе изоморфных подграфов необходимо:

1) описать исходную КС с помощью графовой модели;

2) решить для графа задачу выделения в нем изоморфных подграфов;

3) от полученных результатов решения задачи на графе необходимо перейти к результатам решения задачи типизации в КС.

В случае обработки КС большой размерности с большим числом инвариантных контактов элементов целесообразно исполь­зование гиперграфовой модели.

Алгоритм А. М. Бершадского выделения в графе изоморфных подграфов имеет следующий вид:

1°. Объединяются равноинвариантные вершины графа G = ( X , U ) в группы Г^k_i (к— шаг выделения изоморфных подграфов, начальный шаг k_i = 0).

2°. Определяются группы Г^k_i с мощностью множества, равного 1 (t=1), и производится исключение их из дальнейшего рассмот­рения.

3°. Определяется число возможных объединений групп Г ^k _i : L = l ( l —1)/2, где l—число групп Г^k_i.

4°. Объединяются группы Г^k_i и Г^k_i и определяются группы изоморфных подграфов Г^k_i⁺¹, имеющих мощность t = k + 2. Про­цесс выделения изоморфных подграфов заключается в выборе максимального числа одинаковых (но не нулевых) элементов подматрицы R[Г^k_i \ Г^k_j], расположенных в разных строках и сто­лбцах рассматриваемой подматрицы, где R[Г^k_i \ Г^k_j]— подматрица матрицы R исходного графа, расположенная на пересечении строк, соответствующих вершинам х_iєГ_;, и столбцов, соответству­ющих вершинам х_jєГ_j.

5°. K = K_i +1 означает переход к следующему шагу наращива­ния изоморфных подграфов.

6°. Для каждой полученной на предыдущем шаге группы определяется исходный массив М ^k _i ^­ , содержащий вершины, не вошедшие в группу Г^k_i:

7°. Разбиение массивов М ^k _i ^­на группы равноинвариантныхвершин Г^k_i, аналогично выполняемым в 1°.

8°. Определяются группы Г ^k _Mi с мощностью t =1и исключа­ются из дальнейшего рассмотрения:

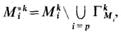
где р— число групп Г ^k _Miс мощностью t=1; М* _i ^К— массив, оставшийся для дальнейшего наращивания изоморфных подгра­фов после исключения групп Г ^k _Miс t =1.

9°. Для каждого массива М* _i ^Кпроверяются условия М* _i ^К ≠0. Если условие для всех массивов не выполняется, то дальнейшее наращивание изоморфных подграфов невозможно, так как от­сутствуют равноинвариантные вершины. В этом случае — переход к 12°. Если хотя бы для одного массива условие выполняется — пе­реход к 10°.

10°. Определяется число возможных объединений групп Г^k_i с группами массивов М _i *. Каждая из групп Г^k_i объединяется только с группами Г^k_Miсвоего исходного массива М* _i ^К :

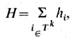
где h_t— число групп Г^k_Miв массиве М* _i ; Т^к— число групп Г ^Kизоморфных подграфов, которые участвуют в дальнейшем наращивании.

11°. Объединение групп Г^k_i и Г^k_Mi и определение групп изоморфных подграфов Г^k_Mi ⁺¹, имеющих мощность t = k + 2 (анало­гично 4°). Переход к 5°.

12°. Конец работы алгоритма.

Рассмотрим пример решения задачи типизации. Во взвешенном графе G * =( X , U ) (рис. 2.4) необходимо выделить максимальное по мощности множество изоморфных подграфов, имеющих максимальное число вершин и ребер.