Для синтеза трехмерных изображений в САПР преимущественно используют средства таких известных систем, как САТІА, Unigraphics, Inventor, Solidworks и др.
Кроме того, применяются графические библиотеки (совокупность подпрограмм, предназначенных для решения задач компьютерной графики) и пакеты компьютерной графики и геометрического моделирования. Такие пакеты представляют собой совокупность методов и средств для создания, обработки и представления (визуализации) графической информации, непосредственно не связанные с проектированием в технике. В проектировании РЭС при разработке и оформлении конструкторской документации наиболее широкое применение находят машиностроительные САПР, имеющие многомодульную структуру, состоящую из групп программ конструкторского проектирования механических объектов, промышленного дизайна, инженерного анализа (функционального моделирования), технологического проектирования, обмена данными, визуализации.
Типичнымипримерами «тяжелых» САПРявляютсяUnigraphics (UGS — Unigraphics Solution), CATIA (DessaultSystemes), Pro/Engineer (PTC — Parametric Technology Corporation). Донедавнеговремениснимиконкурировалисистемы I-DEAS (SDRC), CADDS5 (Computervision) и EUCLID (MatraDatavision). Лидирующееположениевклассе «средних» САПРзанимаютсистемы Solid Works (Solid Works Corporation), Solid Edge (UGS), Inventor (Autodesk). Компания PTC предлагает САПР под названием Pro/Desktop. В России нашли широкое распространение отечественные системы «Компас» («Аскон») и Т-Flex CAD («Топ Системы»), а также некоторые другие системы, в числе которых САПР компаний Autodesk, Beantly, «Интермех», Bee-Pitron. Все эти системы ориентированы в первую очередь на платформу Win- tel, как правило, имеют подсистемы: конструкторско-чертежную 2D, твердотельного 3D геометрического моделирования, технологического проектирования, управления проектными данными, ряд подсистем инженерного анализа и расчета отдельных видов машиностроительных изделий, а также библиотеки типовых конструктивных решений. В приложениях П1 — П5 приведены примеры использования различных программных средств при автоматизированном проектировании РЭС.
МАТЕМАТИЧЕСКИЕ МОДЕЛИ ОБЪЕКТОВ
ПРОЕКТИРОВАНИЯ
В настоящее время нельзя назвать область человеческой деятельности, для которой в той или иной степени не использовались бы методы моделирования. Особенно это относится к проектированию и управлению различными объектами, где процессы принятия решений основаны на получаемой с помощью моделей информации.
Моделирование в широком смысле является основным методом исследования сложных систем и используется для принятия решений в различных сферах инженерного творчества. При этом системы и их части описываются множествами математических моделей, каждая их которых характеризует определенные аспекты и свойства моделируемого объекта.
Компьютерное моделирование можно рассматривать как один из самых мощных методов и инструментов познания, анализа и синтеза, которым располагают проектировщики, ответственные за разработку, производство и функционирование современных РЭС. Идея компьютерного моделирования состоит в замене реального объекта его образом в виде математической модели (ММ), разработки соответствующей программы для ЭВМ и проведения машинных экспериментов с целью получения новых знаний об объекте или решения определенной задачи. При этом у исследователя появляется возможность экспериментировать с моделью системы даже в тех случаях, когда делать это на реальном объекте практически невозможно или нецелесообразно. Работа не с самим объектом или процессом, а с его математической моделью дает возможность относительно быстро и без существенных затрат исследовать его свойства и поведение в любых возможных ситуациях.
Требования к математическим моделям РЭС
Понятие математической модели не имеет строгого формального определения. Обычно под математической моделью объекта понимают совокупность отношений, выраженных при помощисистемы математических символов и обозначений, которые отражают наиболее существенные свойства изучаемого объекта. Процесс моделирования предполагает наличие объекта (системы) исследования, исследователя, перед которым поставлена конкретная задача, и модели, создаваемой для получения информации о системе и необходимой для решения поставленной задачи.
В общем случае РЭС как объект моделирования можно представить кортежем символов, например
РЭС = (ЦН, О, СТР, ТТХ),
где ЦН — целевое назначение; О — оператор; СТР — структура; ТТХ — тактико-технические характеристики.
Целевое назначение определяет перечень задач, решение которых должно обеспечивать РЭС, например, для радиолокационной станции это обнаружение целей, определение их координат, автоматическое сопровождение целей и др.
Оператор системы представляет собой комплекс математических отношений, устанавливающих связи между переменными (входными, фазовыми координатами, выходными) в соответствии с используемыми принципами действия.
Под структурой понимается некоторая организация РЭС, характеризующая ее качественный и количественный состав, множество связей между компонентами, основные свойства компонентов. Важное значение при проектировании имеет геометрическое размещение компонентов в задаваемом объеме или на заданной площади.
Массив тактико-технических характеристик задает количественные значения показателей, определяющих эффективность функционирования радиосистем, например дальность действия, точность, показатели надежности, помехозащищенности и т.д. Для эффективного решения задач проектирования математическая модель должна удовлетворять ряду общих требований, а также требованиям, отражающих специфику РЭС. К основным общим требованиям ММ относятся следующие.
ПолнотаММпозволяет отразить в достаточной мере именно те характеристики и особенности системы, которые интересуют проектировщиков с точки зрения поставленной цели проведения моделирования. Например, модель может полно описывать протекающие в системе процессы, но не отражать ее габаритные, массовые или стоимостные показатели.
Точность ММ дает возможность обеспечить приемлемое совпадение реальных и найденных при помощи ММ значений выходных переменных системы, составляющих вектор у = (у1, у2,... у n )т.
Пусть ум и уэ — найденное при помощи ММ и реальное по результатам эксперимента значения i-й выходной переменной. Тогда относительные погрешности  ММ при одних и тех же значениях входных переменных определяются по формуле
ММ при одних и тех же значениях входных переменных определяются по формуле
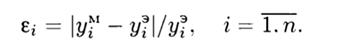

АдекватностьММ— это способность ММ получать выходные переменные системы с погрешностью не более некоторого заранее заданного значения. В общем смысле под адекватностью ММ понимают правильное качественное, структурное и точное количественное описание именно тех характеристик системы, которые наиболее важны в данном конкретном случае.
Экономичность ММоценивают затратами на вычислительные ресурсы (машинное время и память), необходимые для проведения вычислительного эксперимента с ММ на ЭВМ. Эти затраты зависят от числа арифметических операций при использовании модели, от размерности пространства переменных, характеризующих состояние системы и других факторов. Требования экономичности во многих случаях противоречат требованиям высокой точности и адекватности ММ и на практике могут быть удовлетворены лишь на основе разумного компромисса.
РобастностьММхарактеризует ее устойчивость по отношению к погрешностям исходных данных, способность не допускать их чрезмерного влияния на результат вычислительного эксперимента.
ПродуктивностьММсвязана с возможностью получения достоверных исходных данных. Если исходные данные являются результатом измерений, то точность их измерения должна быть не ниже, чем для тех переменных, которые получаются при использовании ММ. В противном случае ММ считается непродуктивной, и ее применение для проектирования РЭС теряет смысл. Наряду с перечисленными требованиями ММ должна обладать следующими свойствами:
• информативностью, т. е. модель должна содержать информацию, достаточную для решения задач проектирования;
• адаптивностью, т. е. приспособленностью к различным значениям входных переменных, параметров элементов, воздействий внешней среды;
• возможностью развития (эволюции) в процессе совершенствования проектируемой системы и др.
Специфические требования к ММ, кроме того, обусловлены особенностями различных классов РЭС, в том числе радиотехнических и оптико-электронных комплексов, предназначенных для радиолокации, радиосвязи, радиоуправления, радионавигации, автонаведения, телевидения, радиосвязи и т. п.
Эти комплексы решают широкий класс задач, в том числе обнаружение целей, сопровождение целей по дальности, направлению и скорости, наведение на цель, передача сообщений на большие расстояния и многие другие.
Главная особенность подобных РЭС состоит в том, что большинство решаемых ими задач связано с созданием и обработкой радиосигналов, анализом их спектров, а также с использованием параметров этих сигналов — частоты, амплитуды, фазы, временного положения и направления прихода. Обработка радиосигналов ведется специальными методами с использованиемгенерирующих, приемно-усилительных и преобразующих устройств. При этом учитываются свойства радиосигналов, обусловленные диапазоном частот, применяемым методом модуляции, наличием амплитудных, фазовых и других искажений, а также влияние помех и шумов.
Радиосигналы, сформированные в процессе изменения одного из параметров, сравниваются с некоторым опорным сигналом. Это требует использования в радиосистемах специальных устройств — дискриминаторов, демодуляторов, фильтров, селекторов. Кроме того, основными элементами многих РЭС являются различные генераторы высокочастотных колебаний, приемные и антенные устройства, а также системы автоматической регулировки усиления, фазовой и частотной автоподстройки передающих и приемных устройств. Поэтому при решении задач анализа и синтеза РЭС широко используются методы спектрального анализа, оптимальной фильтрации, кодирования, выделения полезного сигнала на фоне шума и др.
Специфика ММ РЭС проявляется также при рассмотрении автоматических радиолокационных и оптико-электронных пеленгационных систем, решении задач срыва захвата или слежения, автосопровождения целей, самонаведения и др.
К математическим методам, используемым в РЭС, предъявляют жесткие требования к быстродействию обработки радиосигналов, обусловленному скоростью распространения радиоволн, а также необходимостью рассмотрения их работы в различных состояниях функционирования, учитывающих параметры антенн, помеховую обстановку, метеоусловия, работу других систем и т. п.
При исследовании процессов в РЭС для решения задач проектирования и технологической подготовки производства невозможно учесть все факторы, какие-то требования являются существенными для моделирования, а какими-то можно пренебречь. При этом выдвигается система допущений (гипотез), которая тщательно обосновывается и позволяет выявить и учесть при математическом описании наиболее характерные черты исследуемой системы. В результате формируется ММ проектируемого объекта.
На рис. 4.1 приведена укрупненная схема, отражающая основные этапы работ при построении ММ систем.
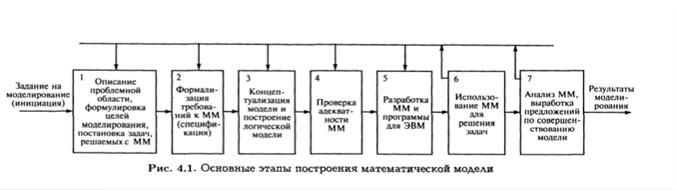
Эта схема содержит этапы, которые являются общими для любых методов построения моделей (аналитических, экспериментальных и др.). Инициацией начала работ являются возникновение какой-либо проблемы (задачи), требующей использования ММ, и получение задания на моделирование.
На первом этапе описывается проблемная область, формулируются цели и задачи, для решения которых требуются ММ. Например, такими задачами могут быть оптимизация конструкции РЭС, оптимизация режимов технологических процессов и т.д.
На втором этапесоставляется полный перечень требований к ММ, по существу, этот перечень представляет собой техническое задание на разрабатываемую модель. Задание должно содержать сведения о входных и выходных переменных, области их изменения, допустимые погрешности, требования к быстродействию и др.
На основе выполнения первых двух этаповразрабатывается концепция модели (третий этап), дается ее вербальное описание, строится схема, учитывающая логические связи между переменными, делаются предположения о методах построения модели.
Четвертый этапявляется самым трудоемким. В зависимости от метода построения ММ этот этап разбивается на несколько под этапов. Например, при использовании экспериментальных методов на этом этапе могут быть выполнены работы по планированию и проведению эксперимента, обработки его результатов и др.
На пятом этапепроверяется адекватность компьютерной программы, разработанной на основе математической модели. Для этого программа тестируется во всем диапазоне изменения переменных. По результатам тестирования и сопоставления с экспериментальными данными делается вывод об адекватности модели или необходимости внесения изменений, т. е. коррекции ранее выполненных этапов.
 Окончательная проверка пригодности модели делается на шестом (завершающем) этапе на основе ее использования для решения задач, сформулированных на первом этапе.
Окончательная проверка пригодности модели делается на шестом (завершающем) этапе на основе ее использования для решения задач, сформулированных на первом этапе.
В процессе компьютерного моделирования исследователь имеет дело с тремя объектами: системой (реальной, проектируемой, воображаемой), математической моделью и программой ЭВМ, реализующей алгоритм решения уравнений модели. Традиционная схема компьютерного моделирования как единого процесса построения и исследования модели, содержащая триаду «модель– алгоритм - программа», представлена на рис. 4.2.
Эффективность компьютерного моделирования во многом зависит от качественного выполнения следующих работ:
• определение (изучение) объекта, т. е. установление границ изменения переменных, ограничений, измерителей эффективности функционирования объекта и т.д.;
• формализация объекта (построение модели), т. е. переход от реального объекта к некоторой логико-математической схеме;
• подготовка данных, необходимых для построения модели, и представление их в соответствующей форме;
• разработка моделирующего алгоритма и программы для ЭВМ;
• оценка адекватности, т. е. определение степени уверенности, с которой можно судить о корректности выводов о реальном объекте, полученных на основании модели;
• стратегическое планирование вычислительного эксперимента для получения необходимой информации;
• тактическое планирование, т. е. определение способа проведения каждой серии испытаний, предусмотренных планом эксперимента;
• проведение вычислительных (имитационных) экспериментов;
• интерпретация и анализ данных машинного моделирования;
• реализация полученных результатов моделирования.
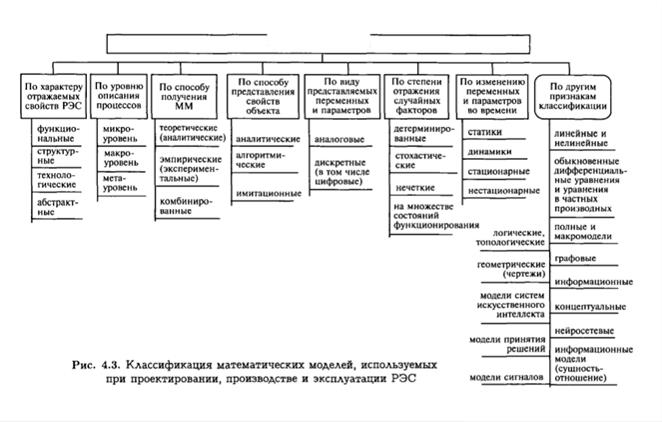
В ходе автоматизированного проектирования и технологической подготовки производства РЭС используется большое число разнообразных математических моделей. Эти ММ классифицируются по разным признакам: по характеру отражаемых свойств разрабатываемого объекта, по отношению к иерархическому уровню, по способу получения и т.д. (рис. 4.3).

Большинство математических моделей предназначено для определения значений выходных переменных исследуемого объекта (вектора у) в зависимости от значений входных управляющих воздействий (вектора х) и воздействий внешней среды (вектора v) при задаваемых параметрах (массив А) объекта, обычно называемых внутренними или функциональными. Такие модели обобщенно записываются в виде
у = F(x, v , А) (4.1)
или как система функций:
у1 = f 1 (x, v , А)
у2 = f 2 (x, v , А) (4.2)
. . . . . . . . . . . .
Функциональные модели вида (4.1), (4.2) широко используются для описания электрических, тепловых, механических и других процессов в РЭС. В общем виде функциональные модели задают как динамические системы (ДС). В простейшем случае ДС представляет собой систему, функционирование которой задается обыкновенными дифференциальными уравнениями в форме Коши обычно с гладкими правыми частями, что гарантирует существование и единственность решения.
Форма Коши- матричная форма записи системы ДУ решенных исключительно относительно первой производной координат САУ:
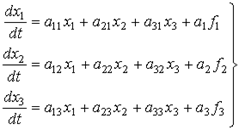 (2)
(2)
где:
- x1, x2, x3 - собственные координаты системы - ошибка системы x(t), воздействие на объект v(t), выходная координата - y(t), ...;
- a11, ... , a33 - постоянные коэффициенты (если система не является зависимой от параметра) - суммы и произведения постоянных времени Tj, коэффициентов усиления Kn;
- f1, f2, f3 - воздействия на систему - сигнал задания g(t), помехи fj(t).
В более сложном случае система обыкновенных дифференциальных уравнений в форме Коши дополняется нелинейными алгебраическими уравнениями и набором вспомогательных формул.
В широком смысле под ДС понимается непрерывно наблюдаемая и изменяющая свое состояние под воздействием внешних и внутренних причин система, которая функционирует в непрерывном времени.
Основными объектами данной модели являются векторы входных переменных (входа)х, фазовых координат (переменных состояния) z, выходных переменных (выхода) у, такие, что
х = (х1, х2,..., х m )Т∈ Х = Х1 ×Х2× . . .×Х m
z = ( z 1 , z2 ,..., zn )Т∈ Z = Z 1 × Z 2 × . . .× Zn
y = (y1, y2,...,yp)Т∈ Y = Y1 ×Y2× . . .× Yp
где X , Z , Y –множества значений векторов x , z, y соответственно;
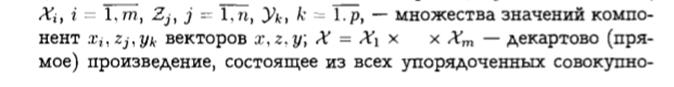
стей вида х = (х1, х2,..., х m ), причем х1 ∈ Х1, х2 ∈ X 2 ,. . ., xm ∈ Xm, аналогичные определения имеют место дляУи Z; т — символ транспонирования вектора. (Транспонированный вектор – вектор, компоненты которого располагаются не столбцом, а в виде строки).
Аналитические модели позволяют построить модели состава и модели структуры системы.
Модель состава ограничивается снизу тем, что считается элементом (из чего состоит), а сверху границей системы. Как эта граница, так и границы разбиения на подсистемы определяются целями построения модели и, следовательно, не имеют абсолютного характера, поэтому существует многообразие моделей состава системы.
Модель структуры описывает существенные связи между элементами (компонентами модели состава).
Эмпирический метод построения математической модели основывается на понятии “чёрный ящик”, введённое У. Р. Эшби.
“Чёрным ящиком” называют систему, внутреннее содержание которой наблюдателю неизвестно, а доступными ему являются только входы и выходы системы.
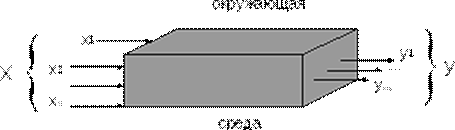
Модель “чёрного ящика”
Эта на первый взгляд простая модель отражает два важных свойства системы: целостность и обособленность от среды.
Представление такой модели осуществляется несколькими способами.
Во многих случаях достаточно содержательного словесного описания входов и выходов; тогда модель “чёрного ящика” является просто их списком.
В других случаях строят количественное описание некоторых или всех входов и выходов. В этом случае тем или иным способом задаются два множества X и Y, например, путём наблюдения за входами и выходами.
Простота модели “чёрного ящика” обманчива, потому что построение такой модели не является тривиальной задачей, так как на вопрос о том, сколько и какие именно входы и выходы следует включать в модель, не всегда однозначны.
Главной причиной множественности входов и выходов в модели “чёрного ящика”, является то, что всякая реальная система, как и любой объект, взаимодействует с объектами окружающей среды неограниченным числом способов. При построении модели из бесчисленного множества входов, выходов, связей отбирается их конечное число. Критерием отбора при этом является целевое назначение модели, существенность той или иной связи по отношению к этой цели.Именно здесь возможны ошибки. Тот факт, что из рассмотрения исключаются остальные связи, не лишает их реальности, и они всё равно действуют.
Нередко оказывается, что казавшееся несущественным или неизвестным при построении модели, на самом деле является важным и должно быть учтено.
Особое значение это имеет при задании цели системы, т.е. при определении её выходов. Это относится к описанию существующей системы по результатам её обследования, и к проекту пока ещё не существующие системы.Для решения этого противоречия главную цель сопровождают заданием дополнительных целей.
Важно подчеркнуть, что выполнение только основной цели не достаточно, что невыполнение дополнительных целей может сделать ненужным или даже вредным и опасным достижение основной цели. Этот момент заслуживает особого внимания, так как на практике часто обнаруживается незнание, непонимание или недооценка важности указанного положения.
Между тем оно является одним из центральных во всей системологии.
Системология — это методологияизучения, проектирования управления и использования природной системности мира и его базовых категорий.
Модель “чёрного ящика” часто называется в ряде случаев единственно применимой при изучении систем в силу объективной невозможности попасть внутрь системы (исследование психики человека) без нарушения её целостности или при действительном отсутствии данных о внутреннем устройстве системы. Например, мы не знаем как “устроен электрон”, но известно, как он взаимодействует с электрическим и магнитными полями, с гравитационным полем. Это и есть описание электрона на уровне модели “чёрного ящика”.
Таким образом, при всём многообразии реальных систем принципиально различных типов моделей, очень немного:
модель типа “чёрного ящика”,
модель состава,
модель структуры,
а также их разумное сочетание и, прежде всего объединение всех трёх моделей, т.е. структурная схема системы:
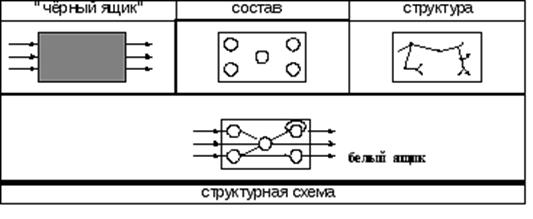
Типы моделей
Можно сказать, что структурная схема “белый ящик” получается как результат “суммирования” всех трёх типов моделей. Все указанные типы моделей являются формальными, относящимися к любым системам и, следовательно, не относящимися ни к одной конкретной системе. Чтобы получить модель определённой технической системы, нужно придать модели конкретное содержание. Процесс построения содержательных моделей является процессом интеллектуальным, творческим.
Дата: 2019-02-19, просмотров: 436.