В настоящее время многие РЭС основаны на цифровой обработке сигналов, радиосистемы имеют процессорные модули, память, интерфейсы, операционную систему и т.д. Архитектура таких РЭС напоминает архитектуру ПЭВМ. Во многом это связано с тем, что практически все радиосистемы в настоящее время содержат автоматические устройства, построенные на базе микропроцессорной техники, которая имеет дело с цифровыми сигналами. Наличие микропроцессора в радиосистеме приводит к необходимости преобразования непрерывных (аналоговых) сигналов, заключающегося в их дискретизации по времени и квантовании по уровню. На выходе отдельных устройств системы цифровые сигналы преобразуются в аналоговые. Такие системы следует рассматривать как непрерывно-дискретные или цифровые системы.

Анализ и синтез цифровых систем требует введения новых понятий, появляются дополнительные элементы в функциональных и структурных схемах системы (аналого-цифровые преобразователи, цифро-аналоговые преобразователи и др.), а также программное обеспечение для микропроцессоров или ЭВМ, используемых в контуре управления. При переходе от описания работы радиосистем обыкновенными дифференциальными уравнениями (непрерывными по времени) к разностным уравнениям, используемым для дискретных систем, возможны качественные изменения свойств системы, в частности из управляемой система может стать неуправляемой. В дискретных системах (ДС) используются различные виды сигналов, получаемых в результате квантования и аналого-цифрового преобразования непрерывного по времени и амплитуде сигнала x(t) (рис. 4.9, а).

К этим сигналам относятся следующие:

• непрерывный по амплитуде и дискретный во времени сигнал (амплитудно-импульсный модулированный сигнал) x(kT₀,h), к = 0.1.2.... с постоянным шагом квантования Т₀ при длительности импульса h (рис. 4.9, б),

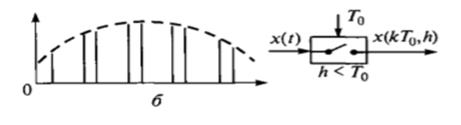
в моменты времени t = кТ₀, к = 0 . 1 .2 ...., для него имеет место

х (кТ_о, h ) = x(t)

• решетчатый непрерывный по амплитуде и дискретный во времени сигнал (амплитудно-модулированный дискретный сигнал) х(кТ_о), получаемый аналогично x(kT₀,h) при h << Т ₀ (рис. 4.9, в),

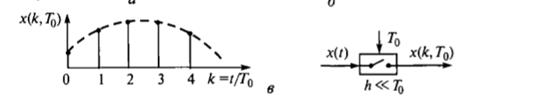
при этом

х(к Т_о) = х(кТ₀, h) = x(t), t = кТ _о , к = 0 . 1 .2 ....;

• дискретный по амплитуде и непрерывный во времени с шагом квантования T ₀ сигнал х_а(кТо) (рис. 4.9, г),

при этом

х_а (кТ _о ) = x(t), t = кТ _о , к = 0,1. 2...:

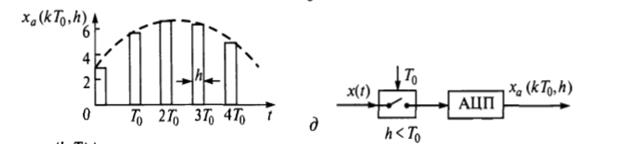
• дискретный по амплитуде и во времени сигнал х _а ( kT ₀ , h ), к = 0.1, 2, (рис. 4.9, д);

• решетчатый дискретный по амплитуде и во времени сигнал (рис. 4.9, е)

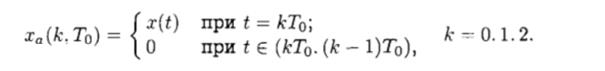
• дискретный по амплитуде и непрерывный во времени (ступенчатый) сигнал x_a ( t ) (рис. 4.9, ж).

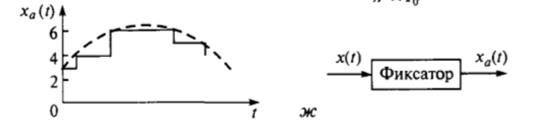
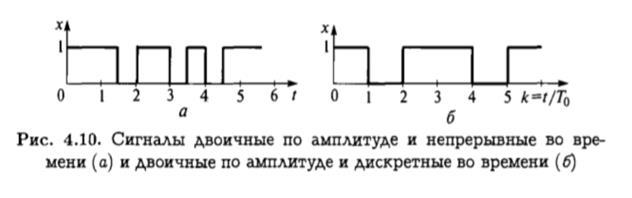
Наряду с перечисленными в дискретных системах могут применяться двоичные по амплитуде и дискретные во времени сигналы (рис. 4.10), поток битов, полосовые цифровые сигналы и др.

В автоматических радиосистемах (АРС) информация поступает в цифровое управляющее устройство в дискретные моменты времени t = кТ ₀ , к = 0,1.2,..., поэтому между моментами дискретизации АРС является разомкнутой, т. е. сигнал y(t) с выхода системы по каналу обратной связи на вход не поступает. Кроме того, обработка информации при формировании сигнала управления приводит к появлению времени запаздывания между у_а(к,Т₀) и u _а (к, То), причем сигнал u(t)зависит не только от алгоритма управления, но и от используемого цифро-аналогового преобразователя. Поэтому система с цифровым управляющим устройством в отсутствие помех не может обеспечить качество работы замкнутой АРС лучше, чем при аналогичной непрерывной АРС.

При рассмотрении ДС обыкновенным дифференциальным уравнениям, описывающим динамические режимы систем с непрерывным временем, соответствуют линейные дискретные модели в виде разностных уравнений, например

При моделировании дискретных устройствразличают синхронные и асинхронные модели.

Синхронные модели состоят из логических уравнений для описания установившихся состояний, в этих моделях переменная времени отсутствует. Их основу составляют логические операции конъюнкции (И), дизъюнкции (ИЛИ) и отрицания (НЕ), реализуемые простейшими элементами цифровых устройств — конъюнктором, дизъюнктором и инвертором (рис. 4.12).

Рис. 4.12

Этим моделям соответствуют синхронные схемы цифровых устройств, передача сигналов в них происходит с частотой синхронизирующих (тактовых) импульсов, которые вырабатываются специальным генератором и подаются на синхровходы устройств. Частота тактовых импульсов выбирается с учетом того, чтобы к моменту прихода нового синхроимпульса переходные процессы, вызванные предыдущим импульсом, практически закончились.

Асинхронные модели также включают логические операции и, кроме того, отражают временные задержки при распространении сигналов элементами и модулями РЭС. В общем виде асинхронная модель логического элемента записывается в виде

y(t) = f_л [x(t — t_зад)],

где f_л — логическая функция; х — входной сигнал; t_зад — время задержки сигнала в элементе.

В динамических системах (ДС) следует различать статические и динамические риски сбоя.

Статические риски сбоя

На рис. 6 показана работа элементовИ и ИЛИ при подаче на их входы двух последовательных во времени наборов Х₁ = x₁x₀= 01 и Х₂ = x₁x₀= 10. Значение сигнала у₁ для элемента И на этих наборах должно оставаться постоянным и равным 0, а у₂ – равным 1. Это выполняется для случаев разброса во времени моментов пере ключения переменных x₁ и x₀, показанных на рис. 6, а и г.

Рис. 6. Разброс во времени моментов переключения

Если же этот разброс соответствует рис. 6, б и в, то видно, что на выходе схемы И появится логический сигнал 1 длительностью Δτ₁, а на выходе схемы ИЛИ - сигнал 0 длительностью Δτ₂. Эти ложные сигналы и являются рисками сбоя, причем видно, что они могут быть, а могут и отсутствовать. Все дальнейшие примеры будут иллюстрироваться временными диаграммами для наихудшего случая, когда риск сбоя обязательно имеет место.

Риск сбоя называется статическим, если у(X₁) = y(Х₂), где y - булева функция. Риск сбоя называется статическим в нуле S₀, если у(X₁) = y(Х₂) = 0. Риск сбоя называется статическим в единице S₁, если у(X₁) = y(Х₂) = 1. Итак, на рис. 6, б имеет место статический риск сбоя в нуле S₀, а на рис. 6, в - статический риск сбоя в единице S₁.

В идеальном случае оба перепада должны приходить в момент времени Тодновременно. Вследствие разброса времени задержек сигналы х₁ и х₂ могут поступить на входы так, как показано на рис. 4.13,б. В этом случае на выходе элемента появляется импульс помехи, который может привести к сбою в работе всего устройства.

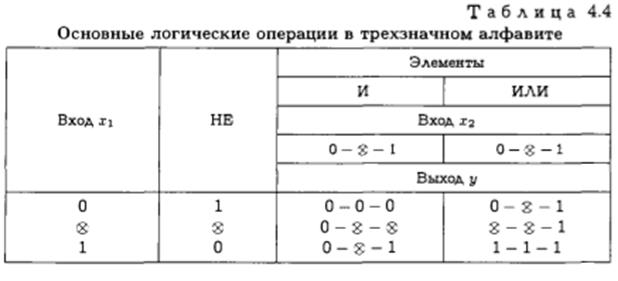
Для выявления и устранения таких рисков сбоя применяют трехзначное синхронное моделирование.

Тремя возможными значениями сигналов х_і и у считают 0, 1, , где

интерпретируется как неопределенность. В табл. 4.4 приведены правила выполнения основных логических операций И, ИЛИ, НЕ в трехзначном алфавите.

На каждом этапе решения уравнений модели элемента при анализе рисков сбоя выполняют двукратное решение, при этом рассматриваются исходные, промежуточные (после первого решения) и итоговые (после второго решения) значения переменных. Для входных сигналов х₁, х₂ допустимы следующие последовательности исходных, промежуточных и итоговых значений: 0 - 0 - 0, 1 – 1-1, 0 — — 1, 1 - 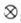- 0. Появление последовательностей 0 -  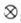- 0 или 1 -  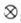- 1 для других переменных означает возможность статического риска сбоя.

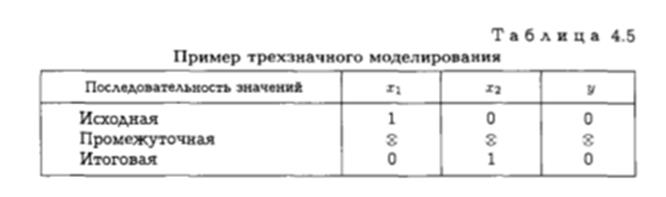
Результаты трехзначного моделирования для диаграммы сигналов (см. рис. 4.13,6) представлены в табл. 4.5.

Трехзначный алфавит может использоваться и в асинхронных моделях, когда неопределенное значение обусловлено случайным разбросом времени задержки t _зад.

Динамический риск сбоя выражается в появлении нескольких перепадов выходного сигнала увместо одного при правильном функционировании схемы.

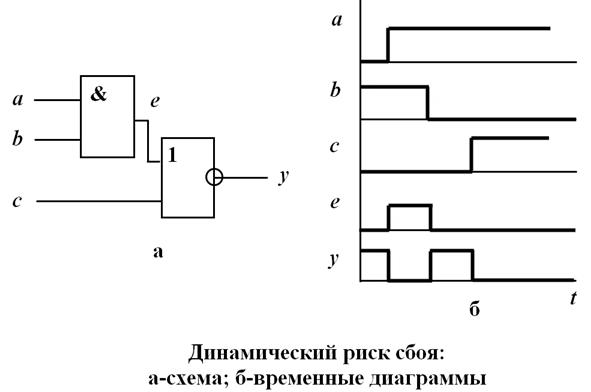
Динамические риски сбоя

На рис. 7, а приведена схема, реализующая функцию у= x₂x₁ + x₀. Пусть входной набор Х₁ = x₂x₁x₀= 010изменяется на входной набор Х₂ = x₂x₁x₀= 101. На рис. 7, б приведены временные диаграммы, соответствующие наихудшему случаю разброса моментов переключения переменных x₂, x₁ и x₀. Поскольку у(X₁) = 0, а y(Х₂) = 1, из рис. 7, б видно, что на выходе схемы имеет место многократное переключение вместо идеального алгоритмического перехода 01. Пусть входной набор Х₁ = x₂x₁x₀= 011изменяется на входной набор Х₂ = x₂x₁x₀= 100. Из рис. 7, в видно, что вместо идеального алгоритмического перехода 10 на выходе имеет место многократное переключение.

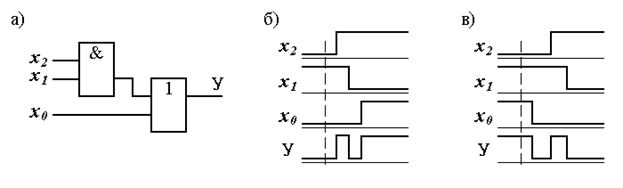
Рис. 7. Наихудший случай разброса во времени моментов переключения

Риск сбоя называется динамическим, если у(X₁) ≠ y(Х₂), где y - булева функция. Риск сбоя называется динамическим D₊ при переходе на выходе 01, если у(X₁) =0, а y(Х₂) = 1. Риск сбоя называется динамическим D_– , если у(X₁) =1, а y(Х₂) = 0. Итак, на рис. 7, б имеет место динамический риск сбоя D₊, а на рис. 7, в - D_–. Из временных диаграмм работы схемы видно, что динамический риск сбоя является следствием статического риска сбоя. Наличие динамических рисков сбоя в цифровой схеме также может привести к нарушению закона ее функционирования.

 Обнаружение динамических рисков сбоя производится аналогично статистическим рискам, но с использованием пятизначного алфавита

{ 0, 1, . E(α) , D ( β) },

где αозначает положительный перепад, β— отрицательный перепад.

В пятизначной логике кроме трех состоянийвводят еще 2 состояния: E и D.

E – переход из состояния 0 в состояние 1,

D – переход из состояния 1 в состояние 0, причем «не Е» = D и «не D» = E,

E∨ 0=E, E∨ 1=1, E∨X=X, E∨D=X; E& 0=0, E& 1=E, E&X=X, E&D=X.

Для D точно такие же формулы бинарных операций. К символам X, E, D так же применимо свойство идемпотентности (Х ∨X = X&X = Х и т.д.).

На динамический риск сбоя указывают появления последовательностей 0 - 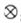 - 1 или 1 -  - 0.

В настоящее время выпускается большое число контроллеров, которые обеспечивают цифровую обработку сигналов и расчет управляющих воздействий для объектов с несколькими входами, а также групп объектов. Эти контроллеры предусматривают функционирование с различными видами сигналов на входе и выходе — цифровыми, аналоговыми, широтно-модулированными и др.