Показателями эффективности обслуживания в зависимости от условий и целей исследуемой задачи могут быть средний процент заявок, получающих отказ и покидающих систему необслуженными;

среднее время ожидания в очереди;

вероятность того, что поступившая заявка будет принята к обслуживанию без ожидания в очереди;

среднее число заявок в очереди (длина очереди) и т.д.

Каждый из этих показателей с той или другой стороны характеризует степень приспособленности системы к выполнению потока заявок, т. е. ее пропускную способность.

В узком смысле под пропускной способностью обычно понимают среднее число заявок, которое система может обслужить в единицу времени.

Наряду с этим используется термин «относительная пропускная способность», который определяется как среднее отношение числа обслуженных заявок к числу поданных.

В общем случае пропускная способность (абсолютная и относительная) зависит как от параметров системы, так и от характера потока заявок.

Если заявки поступают регулярно, т. е. через точно определенные промежутки времени, и обслуживание каждой заявки имеет строго определенную длительность, то расчет пропускной способности системы не представляет особой трудности.

На практике заявки обычно поступают в случайные моменты времени, длительность обслуживания заявок тоже носит случайный характер. Поэтому процесс работы системы протекает нерегулярно, в потоках заявок образуются местные сгущения и разрежения. Сгущения входного потока могут приводить к отказам в обслуживании и к образованию очередей, а разрежения — к непроизводительным простоям отдельных каналов или системы в целом. На эти случайности, вызываемые неоднородностью потока заявок, дополнительно накладываются случайности, связанные с задержками обслуживания отдельных заявок. В результате действия этих факторов процесс функционирования СМО представляет собой случайный процесс. Для решения задач анализа и синтеза СМО, оценки ее пропускной способности необходимо разработать математические модели случайных процессов, протекающих в системе.

Под потоком событий в теории массового обслуживания и надежности понимается последовательность событий, происходящих одно за другим в моменты времени t₁.- t₂. Примеры таких потоков: поток сообщений, последовательно поступающие обращения к базе данных, поток заявок на обслуживание телекоммуникационной сети, поток отказов в автоматической системе и т. п.

В общем случае события, образующие поток, могут быть различными.

Если для моделирования работы СМО рассматривается поток, в котором события различаются лишь моментами появления, то его называют потоком однородных событий. Как уже отмечалось, обычно события происходят в случайные моменты времени, и соответствующий поток событий называется случайным.

Однако в редких случаях возможны регулярные потоки, когда события следуют одно за другим через строго определенные промежутки времени. Регулярный поток сравнительно редко встречается в реальных системах, однако он представляет интерес как предельный случай для других потоков. В последующем, если не оговорено особо, поток событий будет считаться однородным и случайным.

Для моделирования СМО важными свойствами потоков заявок являются следующие.

1. Стационарность. Поток событий называется стационарным, если вероятность попадания определенного числа событий на участок (интервал) времени длиной t зависит только от длины этого участка и не зависит от того, где на оси времени расположен этот участок.

2. Отсутствие последействия. Поток событий называется потоком без последействия, если для любых неперекрывающихся интервалов времени число событий, попадающих на один участок, не зависит от числа событий, попадающих на другие участки времени.

3. Ординарность. Поток событий называется ординарным, если вероятность попадания двух или более событий на элементарный (малый) временной участок Δt пренебрежимо мала по сравнению с вероятностью попадания на этот участок одного события.

Поток событий, обладающий перечисленными тремя свойствами (стационарность, ординарность и отсутствие последействия), называется простейшим или стационарным пуассоновским. Для простейшего потока число событий, попадающих на любой фиксированный интервал времени, распределено по закону Пуассона. Закон распределения Пуассона

Если число испытаний 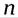увеличивается, то увеличивается число и членов биномиального распределения. Так как сумма вероятностей всех возможных значений остается равной единице, то значение вероятности каждого отдельного значения уменьшается. Этим объясняется то, что закон Пуассона иногда называют законом редких событий.

Определение. Дискретная случайная величина X , возможными значениями которой являются X = m ( m = 0, 1, 2,…), а вероятности соответствующих значений определяются по формуле Пуассона

,

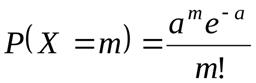называется пуассоновской случайной величиной с параметром a.

Пуассоновское распределение широко используется в теории массового обслуживания. Число aназывается интенсивностью.

Закон распределения Пуассона случайной величины можно записать в виде таблицы 2:                                                         Таблица 2.

	0	1	2	…		…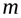
				…		…

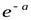
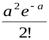
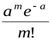
Условию стационарности удовлетворяют потоки, вероятностные характеристики которых не зависят от времени. Для стационарного потока характерна постоянная плотность, т. е. среднее число заявок в единицу времени. На практике часто встречаются потоки, которые могут рассматриваться как стационарные на ограниченном интервале времени. Например, поток вызовов на телефонной станции в определенное время суток (рабочее время или ночное) может считаться стационарным, а в течение целых суток поток уже нельзя считать стационарным.

Условие отсутствия последействия, когда заявки поступают на обслуживание независимо друг от друга, во многих случаях приемлемо для входных потоков. Однако выходной поток обслуженных заявок обычно имеет последействие, даже если входной поток без последействия.

Условие ординарности потока означает, что заявки на обслуживание приходят поодиночке, а не группами (парами, тройками и т. п.). Если в неординарном потоке заявки поступают одинаковыми по составу группами, то его можно свести к ординарному. Для этого достаточно вместо потока отдельных заявок рассмотреть поток групп заявок (пар, троек и т. д.). Если отдельные заявки случайным образом могут оказаться двойными, тройными и т.д., то приходится рассматривать поток разнородных событий.

Простейший поток заявок играет в теории массового обслуживания особую роль, аналогичную роли нормального закона среди законов распределения случайных величин. Известно, что при суммировании большого числа независимых случайных величин, имеющих различные законы распределения, результирующая величина имеет распределение, близкое к нормальному закону. Аналогично при суммировании большого числа ординарных стационарных потоков, имеющих последействие, получается поток, близкий к простейшему. Это имеет место при условии, что складываемые потоки должны оказывать на суммарный поток равномерно малое влияние. Обычно достаточно сложить не менее 4—5 потоков, чтобы получить поток, который можно рассматривать как простейший.

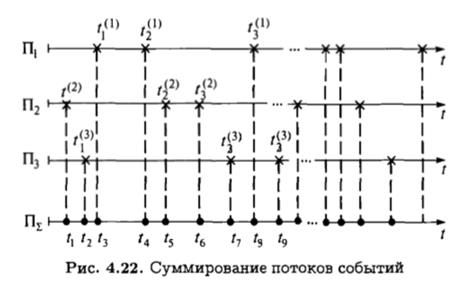
Представим отдельный независимый поток событий П_i как последовательность моментов времени наступления событий (для входного потока — поступления заявок) t₁⁽ⁱ⁾ ,t₂⁽ⁱ⁾.

Тогда суммирование нескольких потоков П_i, i = 1, 2, …,n, заключается в том, что все моменты времени появления событий накладываются на одну временную ось, и для суммарного потока П_Σ можно записать

П_{Σ =}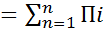

На рис. 4.22 показано суммирование потоков при n = 3.

Широкое использование простейшего потока в теории массового обслуживания объясняется следующим.

Во-первых, простейшие и близкие к ним потоки часто встречаются на практике.

Во-вторых, при потоках заявок, отличающихся от простейших, во многих случаях можно получить приемлемые по точности результаты, если поток любой структуры заменить простейшим с той же плотностью. Для простейшего потока, как уже отмечалось, число точек, попадающих на временной участок τ, распределено по закону Пуассона с математическим ожиданием а = λτ,где λ — плотность потока (среднее число событий, приходящееся на единицу времени). Вероятность того, что за время τ произойдет ровно m событий, определяется по формуле

p_m ( τ ) = [ ( λτ) ^m / m ! ] е ^{- λτ},m = 0,1, 2.

В частности, вероятность того, что участок τ окажется пустым, т. е. m = 0

р_о( τ ) = е^{- λτ}

Случайное время Т между соседними событиями в простейшем потоке подчиняется показательному (экспоненциальному) распределению с плотностью вероятности

Если в простейшем потоке снять ограничение на отсутствие последействия, при этом промежутки времени между последовательными событиями T₁ и Т₂, представляют собой независимые случайные величины, то такой поток называется потоком с ограниченным последействием или потоком Пальма. Модель данного потока широко используется для выходных потоков СМО, а также при анализе надежности систем с резервированием. Например, если входной поток заявок простейший, то поток необслуженных заявок (в результате выбывания вследствие занятости всех каналов СМО) будет потоком с ограниченным последействием.

Большое применение на практике находят модели потоков с ограниченным последействием в виде потоков Эрланга различного порядка, которые образуются «просеиванием» простейшего потока. Если в простейшем потоке «выбросить» каждую вторую точку, то оставшиеся точки образуют поток Эрланга первого порядка; если же в простейшем потоке сохранять каждую третью точку, то получим поток Эрланга второго порядка и т.д.

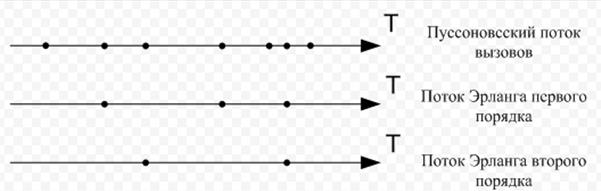
На рис. 4.23, а, б показаны примеры образования таких потоков,

Для потока Эрланга к-то порядка время Тмежду соседними событиями равно сумме к — 1 независимых случайных величин, т. е.

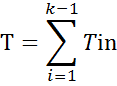
T ₁ ⁿ , T ₂ ⁿ ,…, T _{( k -1)} ⁿ— независимые случайные величины, подчиненные одному и тому же показательному закону с параметром λ (4.16).

В процессе функционирования состояния СМО изменяются скачком. Изменение состояния может быть вызвано приходом новой заявки, освобождением канала в результате обслуживания заявки, уходом заявки из очереди и т. п. Число возможных состояний системы считается конечным, или счетным, обозначим множество таких состояний X = { х_і, і = 0.1,2.3....}.

В любой момент времени t система может находиться только в одном из этих состояний х_і ? X . Вероятность того, что в момент времени t система находится в состоянии х_іобозначимp_i ( t ). Для любого момента времени t должно выполняться условие нормировки

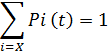
где T — множество номеров состояний системы.

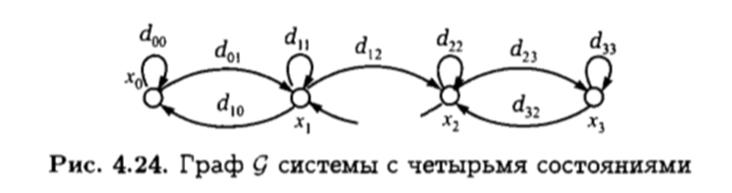
Случайные процессы, протекающие в СМО, обычно представляют собой процессы с непрерывным временем, что связано со случайностью потока заявок. Изменения состояний системы могут быть представлены ориентированным графом Q изменения состояний. Вершины графа соответствуют возможным состояниям, а дуги — переходам из одного состояния в другое за малый промежуток времени dt .

В качестве примера на рис. 4.24 приведен граф Q, отображающий изменение состояний в системе обслуживания с тремя каналами. Система может находиться в четырех состояниях: х0 — все каналы свободны; х1 — один канал занят; х2 — два занято и хз — все три канала заняты. Если система в момент времени t находилась в состоянии х0, то за малое время dt она может перейти в состояние х1 при поступлении заявки (дуга d_oi) или остаться в состоянии x₀ (дуга d₀₀), если заявок не поступало, и т.д.

Если входящий поток заявок пуассоновский и время обслуживания имеет показательное распределение, то для анализа функционирования СМО применяют аппарат марковских случайных процессов.

Процесс называется марковским или процессом без последействия, если для каждого момента времени t ₀ вероятность P(t) любого состояния х системы в будущем, т. е. в момент времени t > t₀, зависит только от состояния системы x(t_o) в настоящий момент t_o и не зависит от того, каким образом система пришла в это состояние.

Марковский процесс в СМО со счетным множеством состояний и непрерывным временем можно описать с помощью системы обыкновенных дифференциальных уравнений, где неизвестными функциями являются вероятности р_i состояний x_і , I = 0,1,2,..