Модели, описывающие физические состояния элементов и частей РЭС и процессы в сплошных средах, т. е. поля электрического потенциала в полупроводниковых кристаллах, распределение температуры в модулях, напряженно-деформированное состояние механических конструкций и т. п., называют математическими моделями на микроуровне или распределенными моделями.

В этих моделях фазовыми координатами (переменными) являются плотности токов, электрические потенциалы, температуры, механические напряжения и т. д., а независимыми переменными — время и пространственные координаты. Математические модели на микроуровне записываются в виде интегральных или дифференциальных уравнений в частных производных, дополненных краевыми (начальными и граничными) условиями. Примерами таких уравнений являются уравнения электродинамики, теплопроводности, упругости и др.

В общем виде модель на микроуровне можно записать следующим образом:

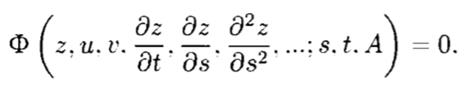
где Ф — оператор связи между переменными и их производными;

z , u , v — векторы фазовых координат, управляющих и внешних воздействий соответственно; s — вектор пространственных координат; t — время; А — массив параметров.

При решении задач моделирования на микроуровне, т. е. определении значений функции z(s, t), соответствующая ММ содержит:

• основноеуравнениеF(z(s,t)) = f(s,t), s ∈ D, t > t_o;

• граничные условия Г (z(s, t)) = g(s, t), s ∈ D_гp. t > t₀;

• начальныеусловияT (z (s,t)) = z(s,t_o), s ∈ D, t = t_o.

Здесь F, Г, T — операторы (линейные) основного уравнения, граничных и начальных условий соответственно; D, D_гp — область определения пространственных координат s и ее граница; t₀ — начальный момент времени; f(s,t) — воздействия на систему; g(s,t) — функции, входящие в уравнения граничных условий.

Наиболее часто употребляемые основные уравнения ММ на микроуровне приведены в табл. 4.1.

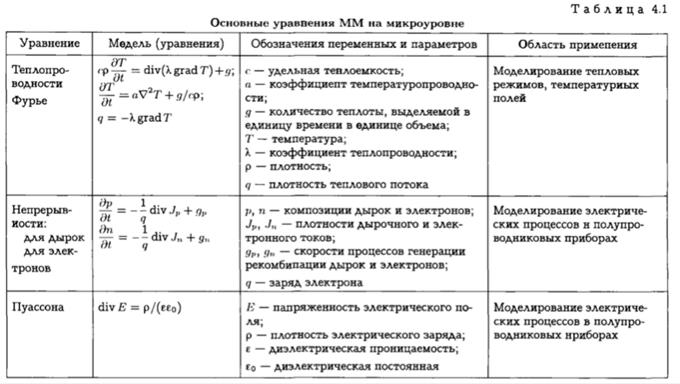
В этих уравнениях переменные Е, H , W, J_p, J_n, G_M и другие являются векторными. Над векторными и скалярными переменными в декартовой системе координат (s₁, s₂, s₃) выполняются следующие операции (в градиенте суммы компонентов):

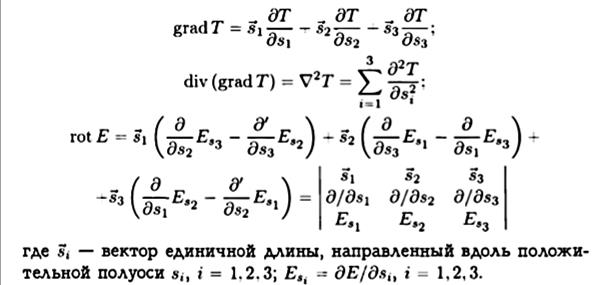
Градиент функции – векторная величина, нахождение которой связано с определением частных производных функции. Направление градиента указывает путь наискорейшего роста функции от одной точки скалярного поля к другой.

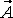Дивергенция (или расходимость) векторного поля в точке М - это предел отношения потока вектора через замкнутую поверхность 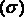окружающую точку М, в направлении ее внешней нормали к объему, ограниченному этой поверхностью, при условии, что вся поверхность 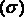, стягивается в точку М:

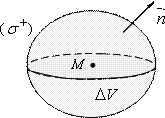
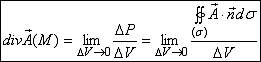
Дивергенция — это линейный дифференциальный оператор на векторном поле, характеризующий поток данного поля через поверхность достаточно малой окрестности каждой внутренней точки области определения поля.

Если v(x, y, z) — поле скорости движения газа (или течения жидкости), то rot v — вектор, пропорциональный вектору угловой скорости бесконечно малой частицы сплошной среды (можно также представить себе вращение пылинки, увлекаемой потоком газа или жидкости).

При этом rot v = 2 ω, где ω — это угловая скорость.Ротор — векторный дифференциальный оператор над векторным полем. Показывает, насколько и в каком направлении закручено поле в каждой точке.

Для решения ММ на микроуровне применяются численные методы, основанные на дискретизации независимых переменных s, t. В результате дискретизации в области непрерывного изменения переменные s, t заменяются множествами значений в узловых точках, которые рассматриваются как узлы некоторой сетки. Поэтому методы решения уравнений в частных производных называют также сеточными. Наибольшее распространение из числа сеточных методов получили метод конечных разностей (МКР) и метод конечных элементов (МКЭ).

При использовании МКР производные в уравнениях модели заменяют конечно-разностными аналогами, для этого с учетом особенностей задачи выбирают вид и шаг сетки, выделяют внутренние и граничные узлы. В результате задача моделирования сводится к решению системы линейных алгебраических уравнений относительно потенциалов в узлах сетки.

Метод конечных элементов представляет собой комбинацию конечно-разностных и проекционных методов. Здесь используется специально построенная система носителей, в качестве которых могут быть треугольные или криволинейные образы. Благодаря этому расширяется класс решаемых задач. Часто метод МКЭ называют проекционно-сеточным. Неизвестные коэффициенты (проекции) в нем определяются методом Бубнова — Галеркина.