При медленном сжимании газа работа, совершаемая внешними телами над газом, будет отличаться только знаком:

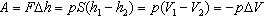
Работа, совершаемая термодинамической системой при постоянном давлении, равна

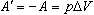Теплоемкость

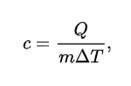Удельная теплоёмкость — это отношение теплоёмкости к массе, теплоёмкость единичной массы вещества (разная для различных веществ); физическая величина, численно равная количеству теплоты, которое необходимо передать единичной массе данного вещества для того, чтобы его температура изменилась на единицу.

Формула расчёта удельной теплоёмкости:

{\displaystyle c={\frac {Q}{m\Delta T}},}где c — удельная теплоёмкость,

Q — количество теплоты, полученное веществом при нагреве (или выделившееся при охлаждении),

m — масса нагреваемого (охлаждающегося) вещества,

ΔT — разность конечной и начальной температур вещества.

На значение удельной теплоемкости напрямую воздействуют несколько компонентов: температура вещества, давление и иные термодинамические характеристики.

Первый закон термодинамики и его применение для изохорного и изобарного процессов в газах. Универсальная газовая постоянная. Уравнение Майера.

Применение первого закона термодинамики к изопроцессам:

При изохорном процессе объем газа не меняется и поэтому работа газа равна нулю. Изменение внутренней энергии равно количеству переданной теплоты:

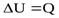
При изотермическом процессе внутренняя энергия идеального газа не меняется. Все переданное газу количество теплоты идет на совершение работы:

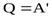
При изобарном процессе передаваемое газу количество теплоты идет на изменение его внутренней энергии и на совершение работы при постоянном давлении.

Адиабатный процесс:

Адиабатный процесс – процесс в теплоизолированной системе. Следовательно, изменение внутренней энергии при адиабатном процессе происходит только за счет совершении работы:

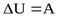
Так как работа внешних сил при сжатии положительна, внутренняя энергия газа при адиабатном сжатии увеличивается, а его температура повышается.

При адиабатном расширении газ совершает работу за счет уменьшения своей внутренней энергии, поэтому температура газа при адиабатном расширении понижается.

Уравнение Майера связывает между собой молярную теплоёмкость для идеального газа в изохорном процессе, и молярную теплоёмкость при в изобарном процессе.

Именно в этом простом уравнении заключена физическая суть величины  R – универсальной газовой постоянной, равной 8,31 Дж/(моль • К).

Запись уравнения Майера

Уравнение Майера

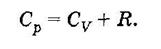
Физический смысл уравнения Майера заключается в том, что при изобарном нагревании газа к нему должна быть подведена большая теплота, чем для такого же изохорного нагревания. Разность теплот должна быть равна работе, совершенной азом при изобарном расширении.