Закон Всемирного тяготения – материальные точки м1 и м2 притягиваются друг к други силами равными произведению их масс и обратно пропорционально квадрату расстояния межу ними.
Вес тела – это сила, с которой тело действует на опору (или подвес) вследствие гравитационного притяжения к Земле. Вес тела проявляется только в том случае, если тело движется с ускорением, отличным от д, т. Е. когда на тело кроме силы тяжести действуют другие силы.
Сила тяжести – сила, действующая на любое материальное тело, находящееся вблизи поверхности Земли или другого астрономического тела.
Вопрос. Сила упругости. Закон Гука. Сила трения.
Момент силы, или вращающий момент, определяется как векторное произведение:
M⃗ =r⃗ ×F⃗
Где F – это вектор силы, лежащий в плоскости вращения, r – радиус-вектор в той же плоскости, направленный от оси вращения к точке приложения силы.
Вопрос. Момент силы.
При любом виде деформации возникает сила, которая стремиться вернуть тело в первоначальное состояние - эта сила и называется силой упругости.
Деформация — изменение формы и объема тела под действием внешних сил. Вида деформации: растяжение, сжатие, кручение, изгиб, сдвиг.
Сила упругости всегда определяется по закону Гука: При упругой деформации растяжения (или сжатия) удлинение тела прямо пропорционально приложенной силе. 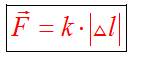 где k — коэффициент упругости или жесткости.
где k — коэффициент упругости или жесткости.
Сила трения
Сила трения равна коэффициенту трения, умноженному на силу реакции опоры.
Fтр=k*N
Fтр – сила трения,  k – коэффициент трения, N – сила реакции опоры.
k – коэффициент трения, N – сила реакции опоры.
Единица измерения силы – Н (ньютон).
Существование силы трения объясняется взаимодействием неровностей на поверхностях тел. Она существует всегда, так как абсолютно гладких тел не бывает.
Сила трения всегда направлена в сторону, противоположную направлению движения, а сила реакции опоры – перпендикулярно поверхности, в сторону, противоположную силе тяжести.  зависит от взаимодействующих материалов и гладкости трущихся поверхностей, но не зависит от площади соприкосновения трущихся тел. Это безразмерная величина.
зависит от взаимодействующих материалов и гладкости трущихся поверхностей, но не зависит от площади соприкосновения трущихся тел. Это безразмерная величина.
Различают силу трения покоя и силу трения движения. Сила трения покоя – минимальная сила, которую нужно приложить для того, чтобы тело начало движение. Сила трения движения – сила, препятствующая движению, если движущая сила станет меньше её, то тело остановится. Если движущая сила равна силе трения, то тело будет двигаться прямолинейно и равномерно.
9 вопрос. Момент инерции материальной точки
и твердого тела.
1) Момент инерции для материально точки – это скалярная величина , определяемая для материальной точки как произведение массы точки на квадрат её расстояния от оси (
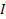 = m
= m 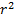 )
)
А для твердого тела производится суммирование моментов инерции всех точек тела (
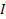 =
= 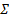 m
m 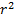 )
)
2) Момент инерции стержня :
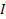 = m
= m 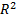
m – масса тела
R – радиус тела
3) Момент инерции кольца :
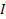 =
= 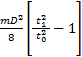
m – масса диска
D – диаметр
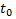 – время , за которое совершается N колебаний диска
– время , за которое совершается N колебаний диска
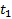 - время , за которое совершается N колебаний системы диск-кольцо
- время , за которое совершается N колебаний системы диск-кольцо
4) Момент инерции диска :
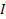 =
= 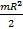
5) Момент инерции шара :
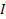 =
= 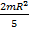
6) Теорема Штейнера :
( Эта теорема используется только в том случае , если ось вращения не проходит через центр масс )
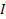 =
= 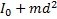
d – расстояние от центра массы до оси вращения
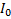 – момент инерции относительно оси , проходящей через центр масс и параллельной оси , относительно которой определяется
– момент инерции относительно оси , проходящей через центр масс и параллельной оси , относительно которой определяется 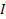 ( момент инерции )
( момент инерции )
10 вопрос. Основное уравнение динамика вращательного движения. 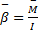
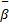 – угловое ускорение
– угловое ускорение
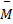 – момент силы
– момент силы
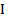 – момент инерции тела
– момент инерции тела
Вопрос. Момент импульса.
Моментом импульса (количества движения) материальной точки А относительно неподвижной точки О называется физическая величина, определяемая векторным произведением:
L = [rp] = [r,mv]
где г — радиус-вектор, проведенный из точки О в точку А; р = mv — импульс материальной точки (рис. 30); L — псевдовектор (см. § 4), его направление со- впадает с направлением поступательно- го движения правого винта при его вращении от r(вектор) к p(вектор).
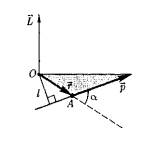
Моментом импульса относительно неподвижной оси z называется скалярная величина Lz , равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки О данной оси. Момент импульса Lz не зависит от положения точки О на оси z.
Момент импульса твердого тела относительно оси есть сумма моментов импульса отдельных частиц: 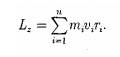
Момент импульса 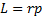 ,
, 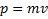 . (в векторном виде)
. (в векторном виде)
Угловые величины: 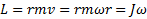 , т.е.
, т.е. 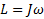 .
.
Закон сохранения момента импульса - суммарный момент импульса систем тел есть величина неизменная: 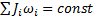
Дата: 2018-12-28, просмотров: 676.