Скорость света одинакова во всех системах отсчета, независимо двигается она или покоится.

Из постулатов можно получить уравнения связывающие координаты и время в разных систеиах отсчета.

Преобразования Лоренца.

22 вопрос. Преобразования Лоренца. Относительность одновременных событий.

Описываемые теорией относительности явления (релятивистские явления) наблюдаются при скоростях движения тел, сравнимых со скоростью с распространения света в вакууме. Классические преобразования Галилея должны быть заменены преобразованиями, удовлетворяющими постулатам теории относительности – преобразованиями Лоренца.

Рассмотрим две инерциальные системы отсчета: K (с координатами х, у, z) и (с координатами , , ), которая движется относительноK (вдоль оси х) со скоростью . В начальный момент времени , когда начала координат 0 и совпадают, излучается световой импульс.

Относительный характер отсчета времени в релятивистской механике. Согласно второму постулату Эйнштейна, скорость света в обеих системах одинакова и равна с. Поэтому, если в системе K за время t сигнал дойдет до некоторой точки А, пройдя расстояние , то в системе координата светового импульса в момент достижения точкиА: 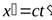, где - время прохождения светового импульса от начала координат до точки А в системе .

Тогда , т.е. (поскольку ).

Вывод: отсчет времени в системах K и различен (в классической физике считается, что время во всех инерциальных системах отсчета течет одинаково, т.е. ); отсчет времени имеет относительный характер.

Преобразования Лоренца имеют вид:

При :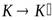

при :

где ;с – скорость света; t – время в системе K; - время в системе ;u - относительная скорость систем K и в направлении осих; (х, у, z) пространственные координаты системы K; - пространственные координаты системы .

Анализ преобразований:

1. Эти уравнения симметричны и отличаются лишь знаком при u.

2. При , они переходят в классические преобразования Галилея – предельный случай преобразований Лоренца.

3. При , выражения длях, t, , теряют физический смысл (становятся мнимыми). Движение со скоростью, большей скорости распространения света в вакууме, невозможно.

4. В закон преобразования координат входит время, а в закон преобразования времени пространственные координаты, т.е. устанавливается взаимосвязь пространства и времени.

Вывод: как расстояние, так и промежуток времени между двумя событиями меняются при переходе от одной инерциальной системы отсчета к другой (в рамках преобразований Галилея эти величины считались абсолютными, не изменяющимися при переходе от системы к системе).

Теория Эйнштейна оперирует не с трехмерным пространством, к которому присоединяется понятие времени, а рассматривает неразрывно связанные пространственные и временные координаты, образующие четырехмерное пространство – время.

В системе К' им соответствуют координа­ты х'₁ и x'₂ и моменты времени t'₁ и t'₂. Если события в системе К происходят в одной точке (х₁=х₂) и являются одновременны­ми (t₁=t₂), то, согласно преобразованиям Лоренца (36.3),

x'₁=x'₂,t'₁=t'₂

т. е. эти события являются одновременны­ми и пространственно совпадающими для любой инерциальной системы отсчета.

Если события в системе К простран­ственно разобщены (х₁¹ х₂), но одновре­менны (t₁=t₂), то в системе К', согласно преобразованиям Лоренца (36.3),

Таким образом, в системе К' эти события, оставаясь пространственно разобщенны­ми, оказываются и неодновременными. Знак разности t'₂- t'₁ определяется знаком выражения v(x₁-x₂), поэтому в различ­ных точках системы отсчета К' (при раз­ных v) разность t'₂-t'₁ будет различной по величине и может отличаться по знаку. Следовательно, в одних системах отсчета первое событие может предшествовать второму, в то время как в других системах отсчета, наоборот, второе событие пред­шествует первому. Сказанное, однако, не относится к причинно-следственным собы­тиям, так как можно показать, что по­рядок следования причинно-следственных событий одинаков во всех инерциальных системах отсчета.

2. Длительность событий в разных системах отсчета. Пусть в некоторой точке (с координатой х), покоящейся относи­тельно системы К, происходит событие, длительность которого (разность показа­ний часов в конце и начале события) t=t₂-t₁, где индексы 1 и 2 соответствуют началу и концу события. Длительность

этого же события в системе К

t'=t'₂-t'₁, (37.1)

причем началу и концу события, согласно (36.3), соответствуют

Подставляя (37.2) в (37.1), получим

Из соотношения (37.3) вытекает, что t<t', т. е. длительность события, проис­ходящего в некоторой точке, наименьшая в той инерциальной системе отсчета, отно­сительно которой эта точка неподвижна. Этот результат может быть еще истолко­ван следующим образом: интервал време­ни t', отсчитанный по часам в системе К', с точки зрения наблюдателя в системе К, продолжительнее интервала т, отсчитан­ного по его часам. Следовательно, часы, движущиеся относительно инерциальной системы отсчета, идут медленнее покоя­щихся часов, т. е. ход часов замедляется в системе отсчета, относительно которой часы движутся. На основании относитель­ности понятий «неподвижная» и «движу­щаяся» системы соотношения для t и t' обратимы. Из (37.3) следует, что замедле­ние хода часов становится заметным лишь при скоростях, близких к скорости света в вакууме.

23 вопрос . Преобразования Лоренца. Относительность длительности событий. Парадокс мезона.

длительность события, происходящего в некоторой точке, наименьшая в той инерциальной системе отсчета, относительно которой эта точка неподвижна.

Парадокс Мезона. Баратья-близнецы.

«Иными словами, близнец, движущийся равномерно и прямолинейно в ракете, старится медленнее, чем его покоящийся брат-домосед.»